Презентація на тему:
Розпізнавання образів на основі мереж Байєса

Розпізнавання образів на основі мереж Байєса Виконавець роботи: студентка групи КА-46м Гуз Наталія Сергіївна Науковий керівник: к.т.н., м.н.с. асистент каф. “ММСА” О. М. Терентьєв НТУУ “КПІ”, Навчально-науковий комплекс “ІПСА” Київ, 2010

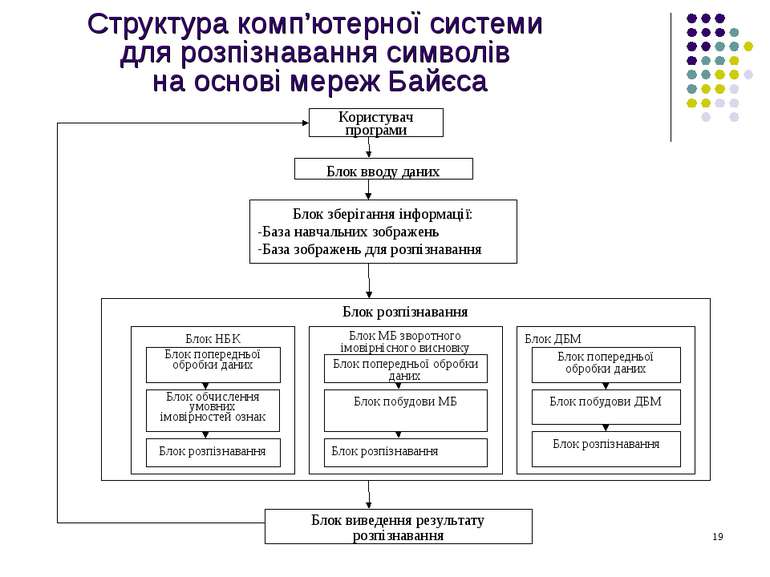
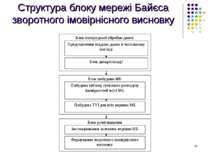
Постановка задачі дослідження Виконання огляду джерел літератури, присвячених розв’язанню задач розпізнавання образів Розробка архітектури комп’ютерної системи для розпізнавання символів з використанням мереж Байєса Розробка методики розпізнавання образів на основі мереж Байєса Реалізація комп’ютерної програми в середовищі програмування Delphi 7на основі запропонованої архітектури комп’ютерної системи та розробленої методики. Апробація розробленої комп’ютерної програми на реальних прикладах.

Задача розпізнавання образів Розпізнавання образів – віднесення вихідних даних до певного класу за допомогою виділення суттєвих ознак або властивостей, що характеризують ці дані, із загальної маси несуттєвих деталей Розпізнавання образів – задачі побудови й застосування формальних операцій над числовими або символьними відображеннями об'єктів реального або ідеального світу, результати розв'язку яких відображають відношення еквівалентності між цими об'єктами. Відношення еквівалентності виражають приналежність оцінюваних об'єктів до деяких класів. Використання систем розпізнавання Медична діагностика Сільське господарство Лінгвістика Ядерна та космічна фізика Автоматизовані системи управління Криміналістика

Історія виникнення розпізнавання образів Початок XX ст. – створення кібернетики (Н. Вінер) 1929 р. та 1933 р.– Густав Таушек та Пол В. Хендел запатентували перші механічні OCR-машини 20-ті роки XX ст. – формування дискримінантного аналізу, як одного з розділів теорії і практики розпізнавання 40-ві роки ХХ ст. – А. М. Колмогоровим і О. Я. Хінчиним поставлена задача про розділення суміші двох розподілів. 50-60-ті роки ХХ ст. – Поява теорії статистичних рішень. В рамках кібернетики виникла нова наука – розпізнавання образів. Перші кроки в області електронного оптичного розпізнавання символів 1952 р. – перший пристрій розпізнавання мовлення (Davies, K.H., Biddulph, R. and Balashek, S.) 1957 р. – перцептрон Розенблатта 1969 р. – в Електротехнічній лабораторії (Японія) почалася розробка проекту "промисловий інтелектуальний робот" 1970-ті роки – розпізнавання формується як самостійний науковий напрямок

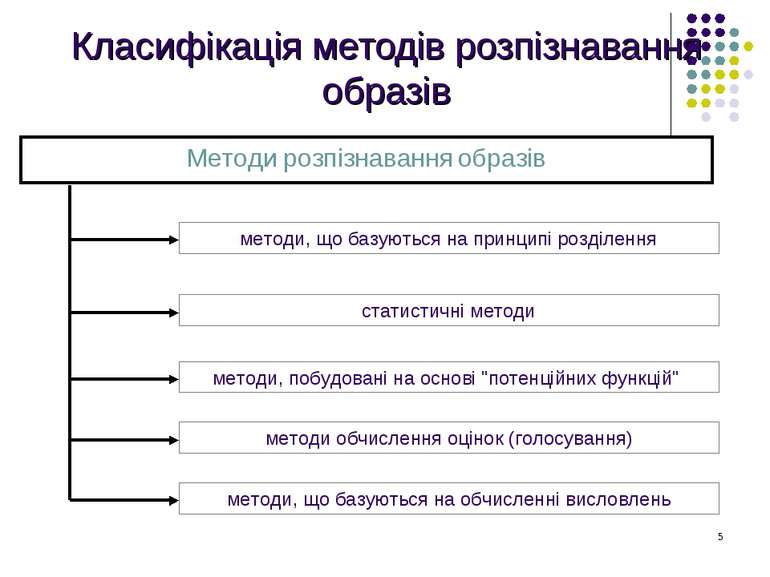
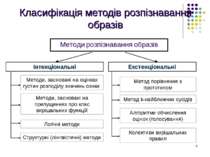
Методи розпізнавання образів методи, що базуються на принципі розділення статистичні методи методи, побудовані на основі "потенційних функцій" методи, що базуються на обчисленні висловлень методи обчислення оцінок (голосування) Класифікація методів розпізнавання образів

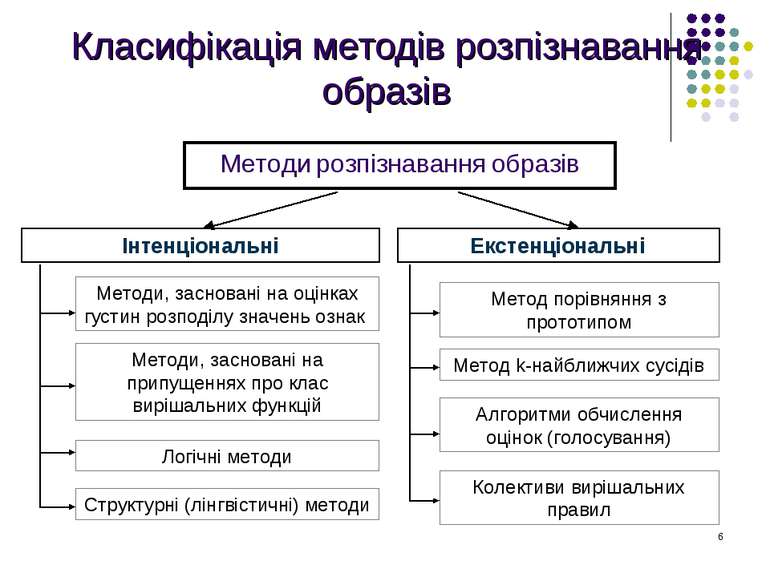
Методи розпізнавання образів Інтенціональні Екстенціональні Методи, засновані на оцінках густин розподілу значень ознак Класифікація методів розпізнавання образів Методи, засновані на припущеннях про клас вирішальних функцій Логічні методи Структурні (лінгвістичні) методи Колективи вирішальних правил Алгоритми обчислення оцінок (голосування) Метод k-найближчих сусідів Метод порівняння з прототипом

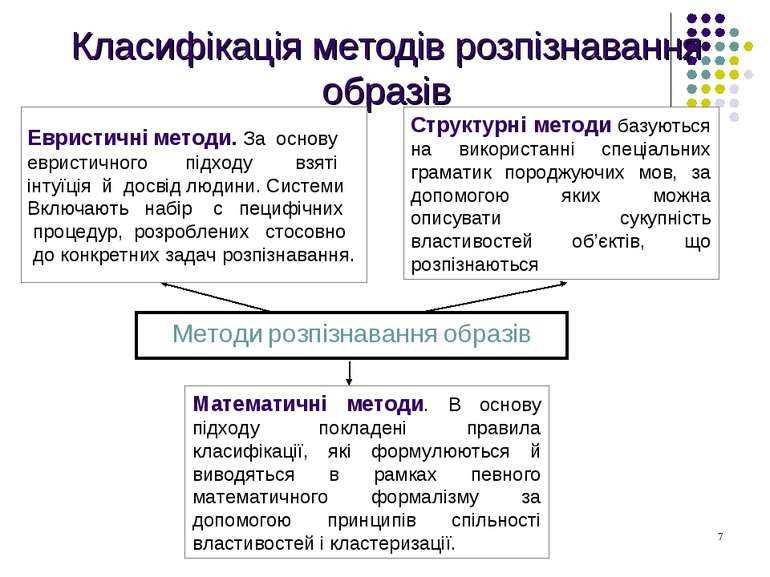
Класифікація методів розпізнавання образів Методи розпізнавання образів Математичні методи. B основу підходу покладені правила класифікації, які формулюються й виводяться в рамках певного математичного формалізму за допомогою принципів спільності властивостей і кластеризації. Структурні методи базуються на використанні спеціальних граматик породжуючих мов, за допомогою яких можна описувати сукупність властивостей об’єктів, що розпізнаються Евристичні методи. За основу евристичного підходу взяті інтуїція й досвід людини. Системи Включають набір с пецифічних процедур, розроблених стосовно до конкретних задач розпізнавання.

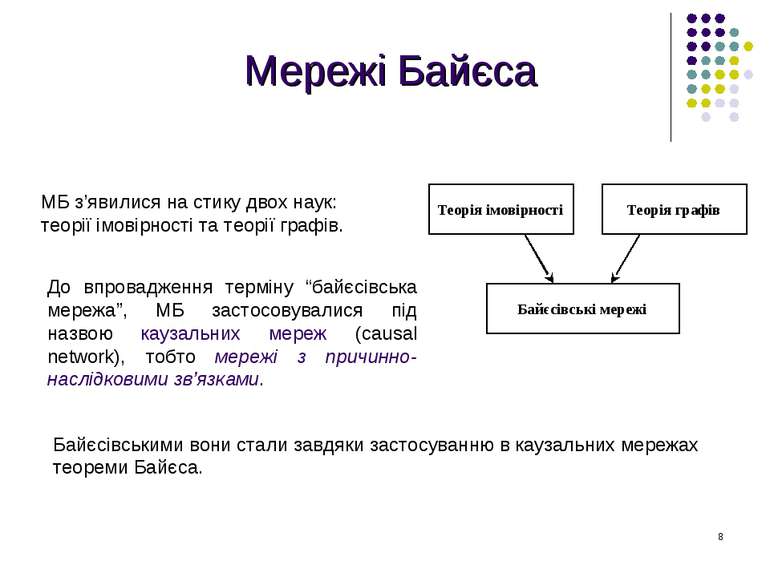
Мережі Байєса До впровадження терміну “байєсівська мережа”, МБ застосовувалися під назвою каузальних мереж (causal network), тобто мережі з причинно-наслідковими зв’язками. МБ з’явилися на стику двох наук: теорії імовірності та теорії графів. Байєсівськими вони стали завдяки застосуванню в каузальних мережах теореми Байєса.

Мережі Байєса Мережа Байєса - це графічна модель процесу або об'єкта довільної природи, представлена парою . G – спрямований ациклический граф, що відповідає випадковим змінним об'єкта або процесу. B – множина параметрів, що визначають мережу. Кожній вершині МБ відповідає таблиця умовних імовірностей. Основним завданням мереж Байєса є представлення розподілу імовірностей над змінними в зручному для обробки та компактному вигляді

Навчання мереж Байєса

Наївний байєсівський класифікатор Теорема Байєса: Наївний байєсівський класифікатор – це простий імовірнісний класифікатор, який грунтується на застосуванні теореми Байєса зі строгим (наївним) припущенням про незалежність.

Алгоритм застосування наївного байєсівського класифікатора для розпізнавання символів Крок 1. Вхідні зображення перетворюються у вектори розмірності n2. а) Зображення розбивається на n клітинок у довжину та n клітинок у ширину. б) Приведення зображення до чисельного вигляду. в) Дискретизація. Кожній клітинці ставиться у відповідність змінна ознаки Пі. Крок 2. Умовна ймовірність кожної ознаки знаходиться за формулою: де n[A=aj , Пi=pi] – кількість появ конкретного значення pi ознаки Пi для символу аj , n[A=aj] – кількість появ символу aj Крок 3. Обчислення умовних імовірностей усіх можливих значень змінної А.

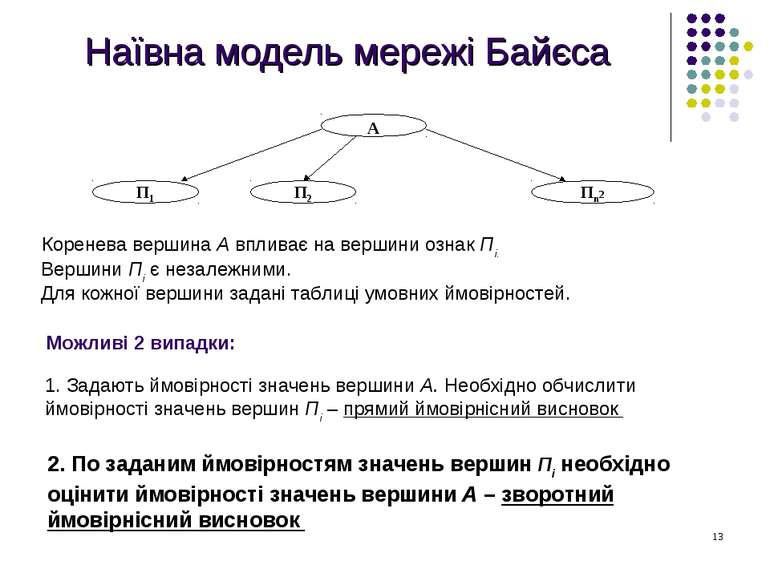
Наївна модель мережі Байєса Коренева вершина А впливає на вершини ознак Пі. Вершини Пі є незалежними. Для кожної вершини задані таблиці умовних ймовірностей. Можливі 2 випадки: 1. Задають ймовірності значень вершини А. Необхідно обчислити ймовірності значень вершин Пі – прямий ймовірнісний висновок 2. По заданим ймовірностям значень вершин Пі необхідно оцінити ймовірності значень вершини А – зворотний ймовірнісний висновок

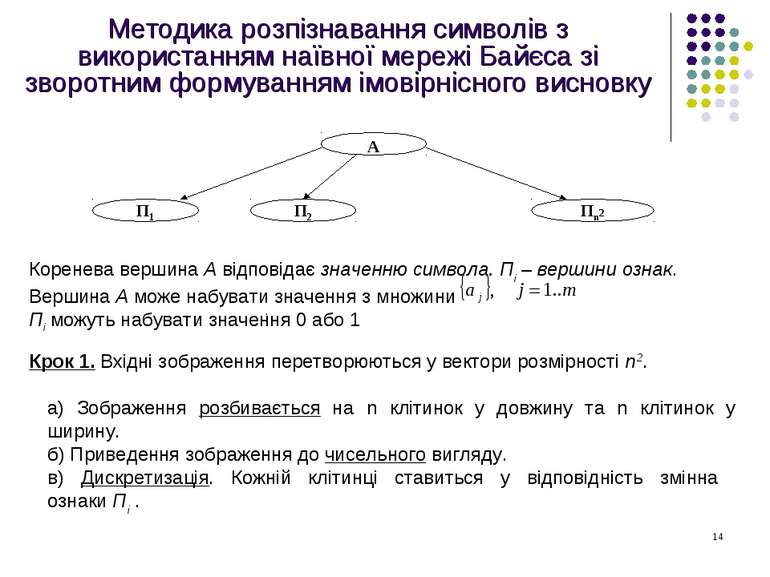
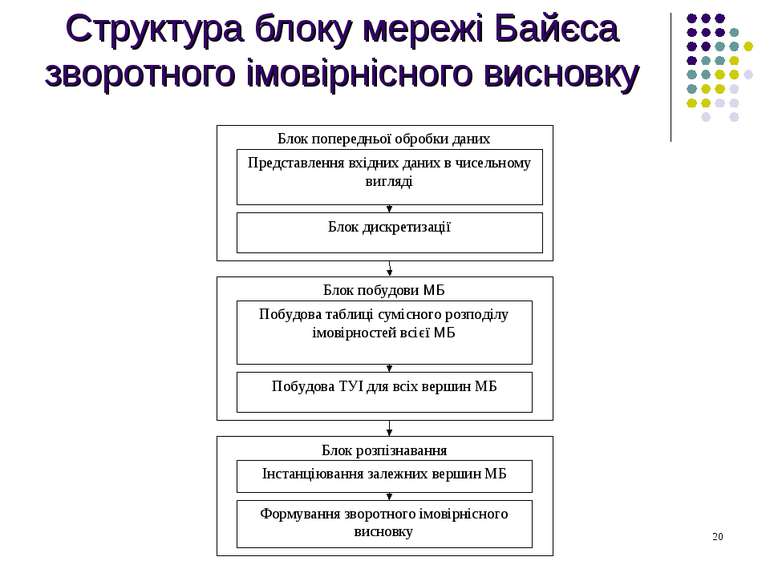
Методика розпізнавання символів з використанням наївної мережі Байєса зі зворотним формуванням імовірнісного висновку Коренева вершина А відповідає значенню символа. Пі – вершини ознак. Вершина А може набувати значення з множини Пі можуть набувати значення 0 або 1 . Крок 1. Вхідні зображення перетворюються у вектори розмірності n2. а) Зображення розбивається на n клітинок у довжину та n клітинок у ширину. б) Приведення зображення до чисельного вигляду. в) Дискретизація. Кожній клітинці ставиться у відповідність змінна ознаки Пі .

Методика розпізнавання символів з використанням наївної мережі Байєса зі зворотним формуванням імовірнісного висновку Крок 2. Побудова таблиці сумісного розподілу імовірностей всієї МБ. Крок 3. На основі значень сумісного розподілу імовірностей всієї МБ, за теоремою Байєса, відбувається побудова ТУІ для всіх вершин МБ. Крок 4. Інстанціювання залежних вершин МБ відповідними значеннями для зображення, яке розпізнається. Крок 5. Формування зворотного імовірнісного висновку. Модель множинної регресії: де Крок 6. Серед можливих значень кореневої вершини обирається значення з найбільшою імовірністю.

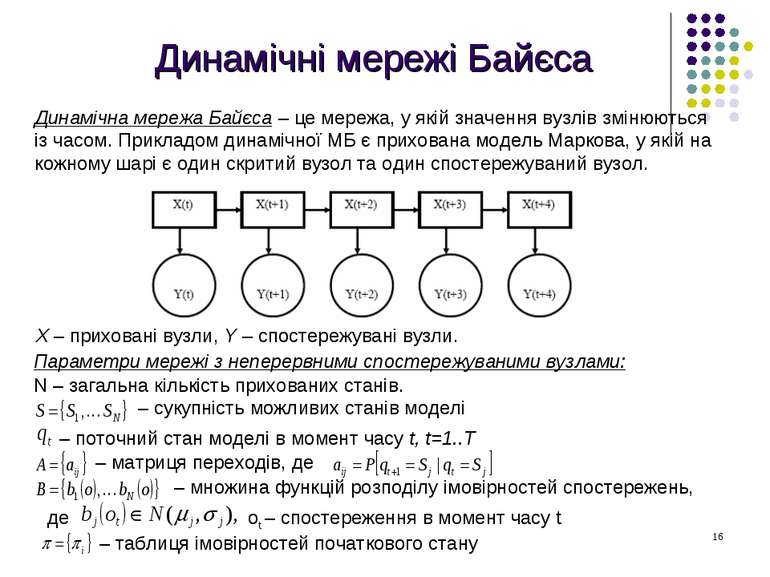
Динамічні мережі Байєса Динамічна мережа Байєса – це мережа, у якій значення вузлів змінюються із часом. Прикладом динамічної МБ є прихована модель Маркова, у якій на кожному шарі є один скритий вузол та один спостережуваний вузол. Х – приховані вузли, Y – спостережувані вузли. Параметри мережі з неперервними спостережуваними вузлами: N – загальна кількість прихованих станів. – сукупність можливих станів моделі – поточний стан моделі в момент часу t, t=1..T – матриця переходів, де – множина функцій розподілу імовірностей спостережень, де ot – спостереження в момент часу t – таблиця імовірностей початкового стану

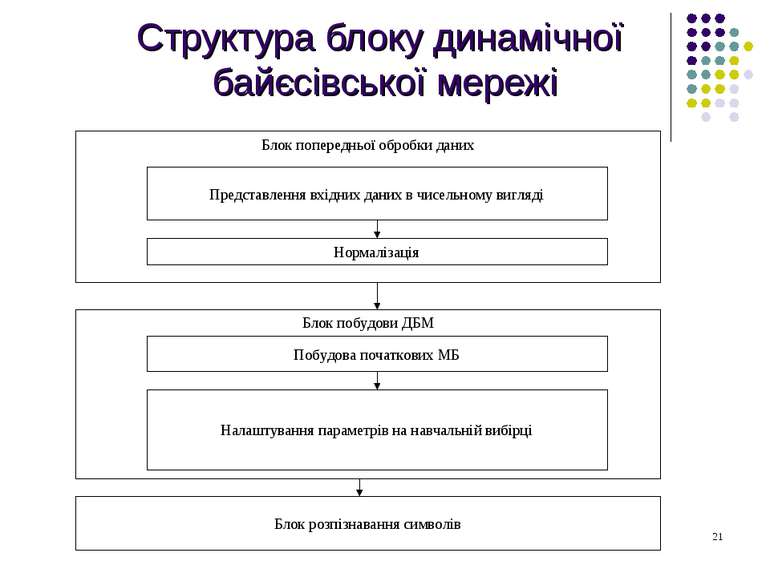
Методика розпізнавання символів з використанням динамічних мереж Байєса Крок 1. Представлення зображень з навчальної та тестової вибірки у вигляді множини спостережень. Крок 2. Для кожного символа будується окрема МБ з випадковими значеннями параметрів. Крок 3. Вибір навчальної послідовності спостережень для символа. Крок 4. Корегування невідомих параметрів мережі – алгоритм Баума-Велха. а) Обчислення прямої процедури: б) Обчислення зворотної процедури:

Методика розпізнавання символів з використанням динамічних мереж Байєса Крок 6. Перевірка завершення алгоритму Баума-Велxа Крок 7. Якщо було виконано навчання МБ кожного символу, навчання завершено. Інакше обираємо МБ наступного символу та переходимо на крок 4. Крок 8. Розпізнавання. Множину спостережень з тестової вибірки пред’являють МБ кожного символа. Крок 5. Перевірка виконання навчання на всіх навчальних послідовностях спостережень даного символа. Якщо всі зображення з навчальної вибірки були використані для навчання, переходимо на крок 6, інакше – на крок 3 в) Обчислення допоміжних змінних: г) Оновлення значень параметрів:

Структура комп’ютерної системи для розпізнавання символів на основі мереж Байєса

Структура блоку мережі Байєса зворотного імовірнісного висновку

Структура блоку динамічної байєсівської мережі

Архітектура пристрою для розпізнавання зображень на основі мереж Байєса

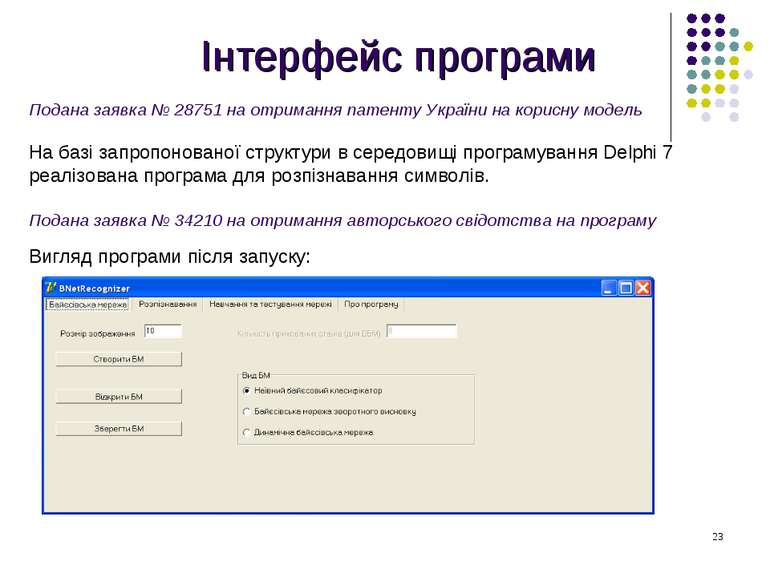
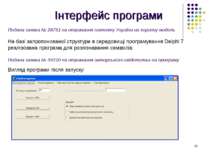
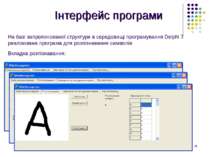
Інтерфейс програми Подана заявка № 28751 на отримання патенту України на корисну модель На базі запропонованої структури в середовищі програмування Delphi 7 реалізована програма для розпізнавання символів. Подана заявка № 34210 на отримання авторського свідотства на програму Вигляд програми після запуску:

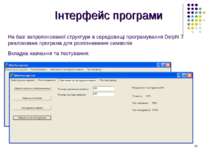
Інтерфейс програми На базі запропонованої структури в середовищі програмування Delphi 7 реалізована програма для розпізнавання символів Вкладка навчання та тестування:

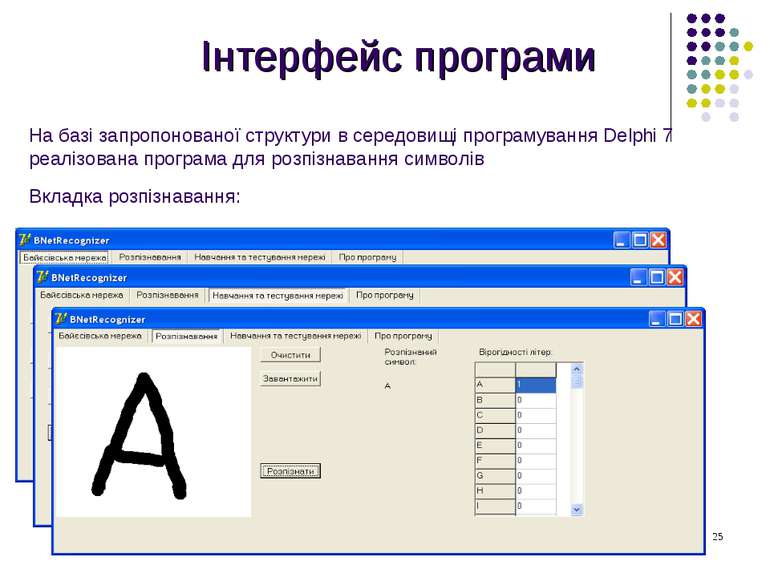
Інтерфейс програми На базі запропонованої структури в середовищі програмування Delphi 7 реалізована програма для розпізнавання символів Вкладка розпізнавання:

Розпізнавання старих друкованих символів Для перевірки якості роботи системи було використано базу даних Google Patent Search, з якої було взято набір з 10 відсканованих патентів, а саме з кожного патенту використано перша сторінка. Вибірка складалася зі 700 окремих зображень для 26 друкованих маленьких літер англійського алфавіту. Вибірка розділялася на навчальну та перевірочну випадковим чином. Зображення, які використовувалися в навчальній вибірці, в тестовій вибірці не зустрічалися. Характеристики ЕОМ: - процесор Intel Core 2 Duo CPU 2,33 GHz оперативна пам’ять 2 GB встановлена операційна система Windows XP 2003 SP2 Приклади зображень:

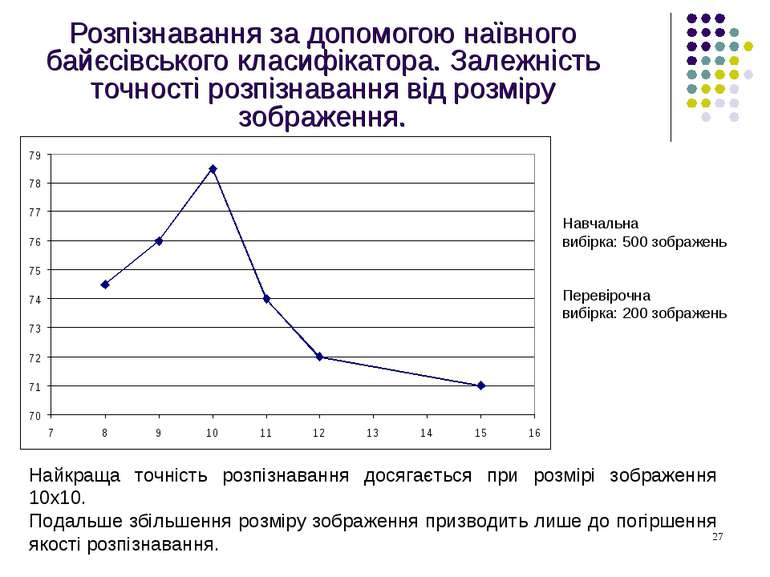
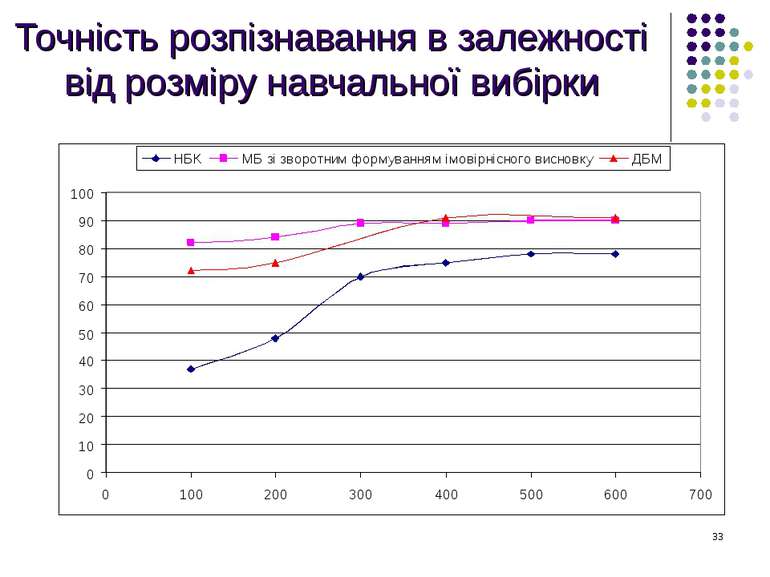
Розпізнавання за допомогою наївного байєсівського класифікатора. Залежність точності розпізнавання від розміру зображення. Навчальна вибірка: 500 зображень Перевірочна вибірка: 200 зображень Найкраща точність розпізнавання досягається при розмірі зображення 10х10. Подальше збільшення розміру зображення призводить лише до погіршення якості розпізнавання.

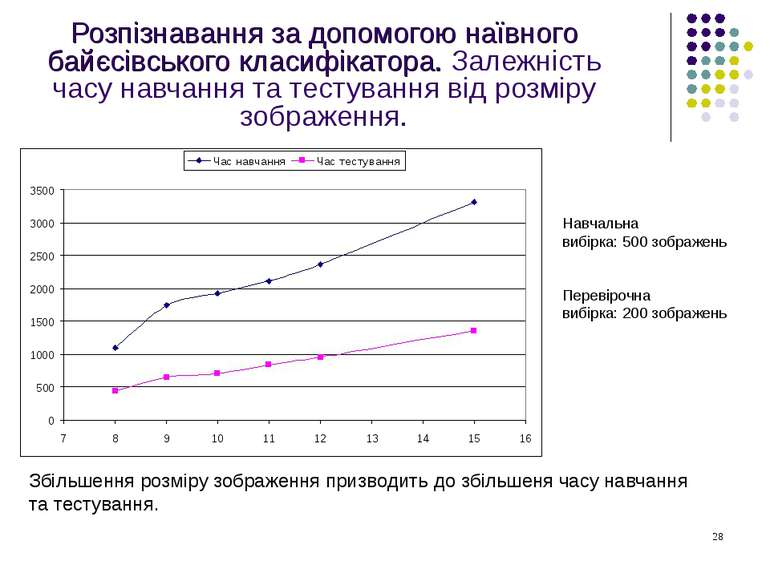
Розпізнавання за допомогою наївного байєсівського класифікатора. Залежність часу навчання та тестування від розміру зображення. Навчальна вибірка: 500 зображень Перевірочна вибірка: 200 зображень Збільшення розміру зображення призводить до збільшеня часу навчання та тестування.

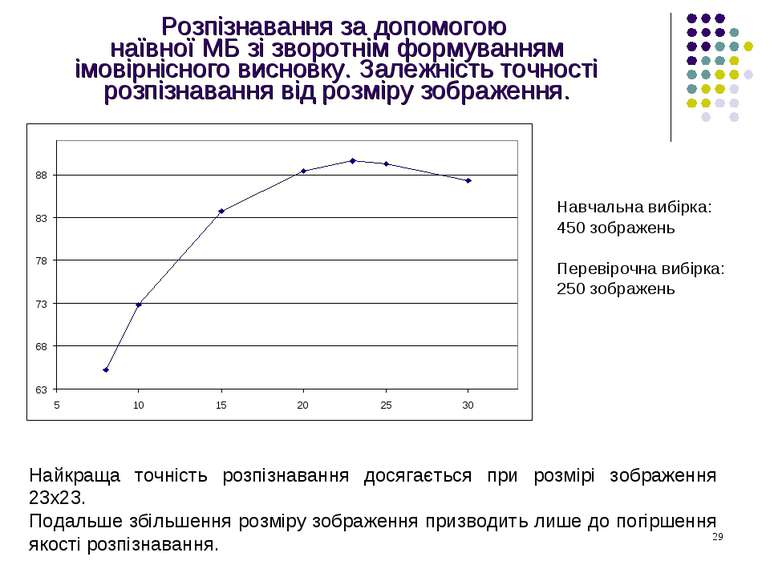
Розпізнавання за допомогою наївної МБ зі зворотнім формуванням імовірнісного висновку. Залежність точності розпізнавання від розміру зображення. Навчальна вибірка: 450 зображень Перевірочна вибірка: 250 зображень Найкраща точність розпізнавання досягається при розмірі зображення 23х23. Подальше збільшення розміру зображення призводить лише до погіршення якості розпізнавання.

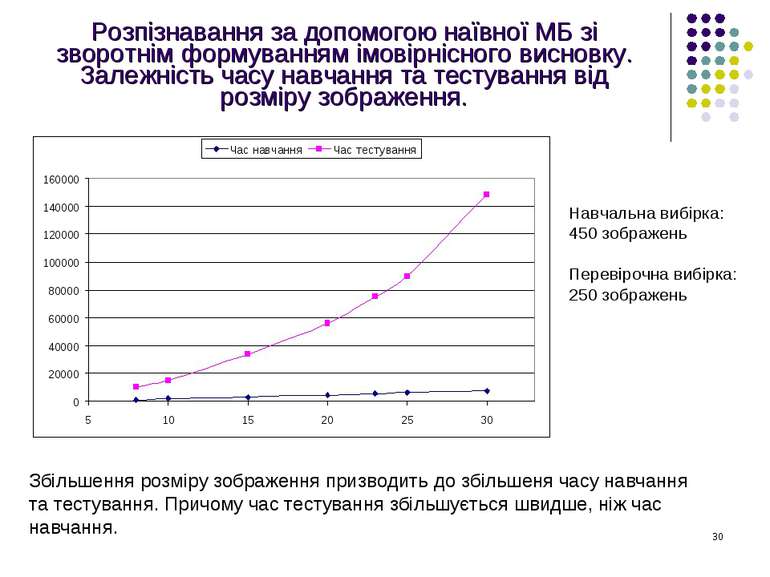
Розпізнавання за допомогою наївної МБ зі зворотнім формуванням імовірнісного висновку. Залежність часу навчання та тестування від розміру зображення. Навчальна вибірка: 450 зображень Перевірочна вибірка: 250 зображень Збільшення розміру зображення призводить до збільшеня часу навчання та тестування. Причому час тестування збільшується швидше, ніж час навчання.

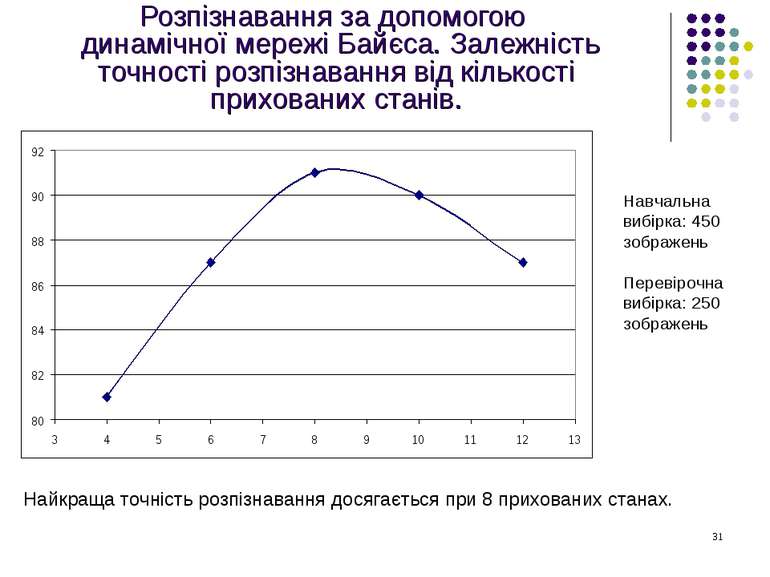
Розпізнавання за допомогою динамічної мережі Байєса. Залежність точності розпізнавання від кількості прихованих станів. Навчальна вибірка: 450 зображень Перевірочна вибірка: 250 зображень Найкраща точність розпізнавання досягається при 8 прихованих станах.

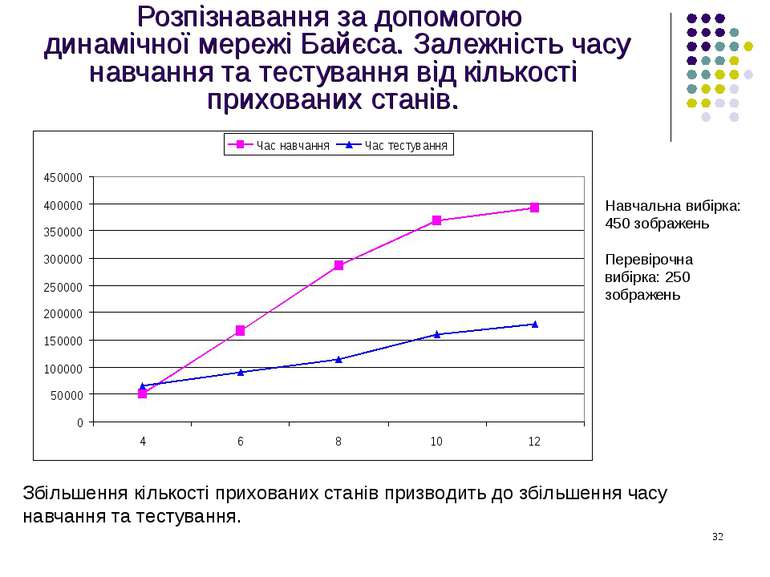
Розпізнавання за допомогою динамічної мережі Байєса. Залежність часу навчання та тестування від кількості прихованих станів. Навчальна вибірка: 450 зображень Перевірочна вибірка: 250 зображень Збільшення кількості прихованих станів призводить до збільшення часу навчання та тестування.

Точність розпізнавання в залежності від розміру навчальної вибірки

Приклади помилок при розпізнаванні Зображення Правильне значення Результат розпізнавання НБК МБ зворотного висновку ДБМ Fine Reader t r t t t d a d d J b a h b b t t t l t

Порівняння результатів розпізнавання

Найкращі результати розпізнавання показала програма ABBY FineReader Реалізовані динамічна мережа Байєса та мережа зі зворотним формуванням імовірнісного висновку показали прийнятні результати Час розпізнавання одного символа для динамічної мережі Байєса є найбільшим Найгірші результати показав наївний байєсівський класифікатор Порівняння результатів розпізнавання

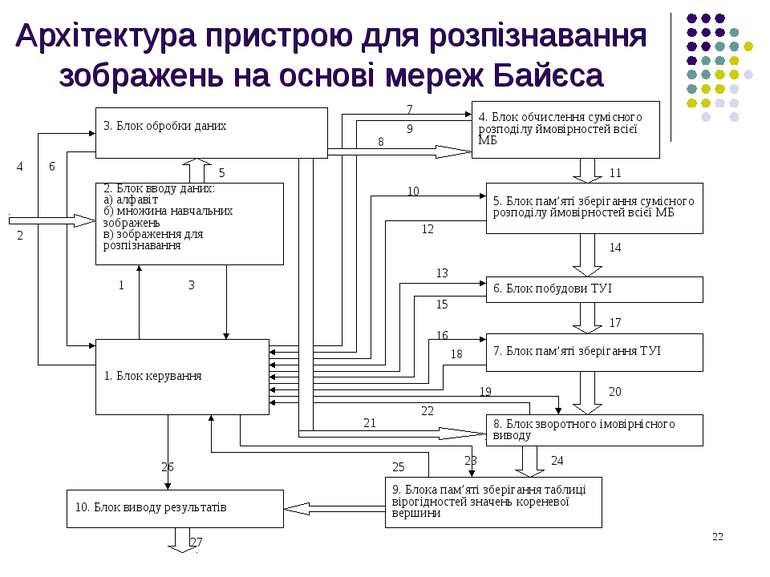
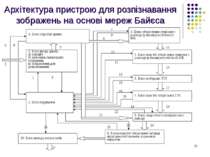
Висновки Запропонована методика розпізнавання образів на основі наївної мережі Байєса зі зворотним формуванням імовірнісного висновку Запропонована методика розпізнавання образів на основі динамічної мережі Байєса Запропонована архітектура пристрою для розпізнавання символів з використанням мереж Байєса Реалізована комп’ютерна програма Розроблена комп’ютерна програма апробована на реальних прикладах.

Рекомендації щодо подальших досліджень Поліпшення використаних для розпізнавання методів: Підбір оптимального розміру зображень Підбір оптимальної кількості прихованих станів На основі реалізованої комп’ютерної програми реалізувати систему для розпізнавання друкованого тексту Застосування інших методів для розпізнавання образів

Публікації Участь у ХІI Міжнародній науково-технічній конференції “Системний аналіз та інформаційні технології ” - 2010 рік Участь у Х Міжнародній науковій конференції “Інтелектуальні системи прийняття рішень і проблеми обчислювального інтелекту” – 2010 рік Подана для опублікування стаття в журнал “Wireless Sensor Network” M. Z. Zgurovskii, O.M. Terentyev, O.A. Akulinina, N.S. Guz. Methods of constructing probability inference in Bayesian networks using LS approach. Дата опублікування осінь-зима 2010 року.

Публікації Подана до опублікування стаття в журнал "Вісник Університету «Україна»" Бідюк П.І., Акулініна О.А., Гуз Н.С., Свердел К.О. Побудова ймовірнісного висновку в мережах Байєса на основі LS-методу. Подана заявка на одержання патенту на корисну модель “Пристрій для розпізнавання символів на основі мереж Байєса» Подана заявка на одержання свідотства на програму для розпізнавання зображень “BNetRecognizer”. Заявка № 34201 від 7 травня 2010 року

Дякую за увагу!