Презентація на тему:
Підвищення ефективності стиснення RGB-зображеньу форматі PNG

Здобувач: аспірант РДГУ Шпортько Олександр Володимирович Науковий керівник: д.т.н., проф. Бомба Андрій Ярославович Підвищення ефективності стиснення RGB-зображень у форматі PNG Доповідь за результатами дисертаційного дослідження за спеціальністю 01.05.03 – математичне та програмне забезпечення обчислювальних машин і систем на здобуття наукового ступеня кандидата технічних наук

Обгрунтування Вступ Актуальність роботи на сьогодні в Інтернеті нараховується більше 16 млн. web-сторінок, що містять зображення у форматі PNG; щороку кількість таких сторінок збільшується на понад 1 млн. Факти, що підтверджують актуальність теми дослідження: Теоретичною та методологічною основою роботи стали праці К. Шенона, Д. Кнута, Д. Хафмана, Я. Зіва, А. Лемпела, Е. Прета, Р. Гонсалеса, Р. Вудса, Д. Селомона, Дж. Міано, Т. Боутела, Д. Ватоліна, А. Ратушняка, М. Смірнова, В. Юкіна, а також аналіз функціонування існуючого програмного забезпечення для стиснення зображень.

Метою дослідження є підвищення ефективності стиснення зображень у форматі PNG як за допомогою вдосконалення і врахування взаємодії використаних алгоритмів компресії, так і шляхом застосування альтернативних чи нових методів кодування. Об'єкт дослідження – методи, алгоритми та програмне забезпечення для стиснення даних без втрат. Предмет дослідження – методи, алгоритми та програмне забезпечення для стиснення 24-бітних RGB-зображень у форматі PNG. Обгрунтування Вступ Мета і завдання дослідження Мета і завдання дослідження

Структура Вступ Структура роботи Структура дисертації: Вступ Розділ 1. Шляхи підвищення ефективності стиснення зображень у форматі PNG. Аналіз літературних джерел. Постановка завдань дослідження Розділ 2. Прискорення стиснення зображень у форматі PNG Розділ 3. Зменшення коефіцієнтів стиснення RGB-зображень у форматі PNG Розділ 4. Модифікації формату PNG для підвищення ефективності стиснення RGB-зображень Висновки

Структура Розділ 1 Структура розділу Розділ 1. Шляхи підвищення ефективності стиснення зображень у форматі PNG. Аналіз літературних джерел. Постановка завдань дослідження 1.1. Послідовність кодування даних зображень 1.2. Словниковий алгоритм LZ77 та основні варіанти його розкладу вхідного потоку 1.3. Кодування Хафмана та його альтернативи 1.4. Предиктори та їх використання 1.5. Додаткові методи зменшення міжелементної надлишковості, що можуть застосовуватися у форматі PNG 1.6. Тестові набори файлів зображень, апаратне, системне та прикладне програмне забезпечення для апробації розроблених алгоритмів 1.7. Висновки до розділу

Застосування предикторів Стиснення словниковим контекстно-залежним алгоритмом LZ77 Стиснення контекстно-незалежними кодами Хафмана Етапи кодування зображень у форматі PNG: Розділ 1 Теоретичні основи Розділ 1 1.1. Послідовність кодування даних зображень

у випадку виявлення для чергової послідовності елементів буфера співпадаючої послідовності у словнику кодують її парою чисел , інакше записують у закодовані дані перший елемент буфера без змін; переносять закодовані елементи з початку буфера в кінець словника; ітеративно продовжують кодування до закінчення елементів буфера. Кроки алгоритму LZ77 для формування розкладу вхідного потоку елементів: Розділ 1 Теоретичні основи 1.2. Словниковий алгоритм LZ77

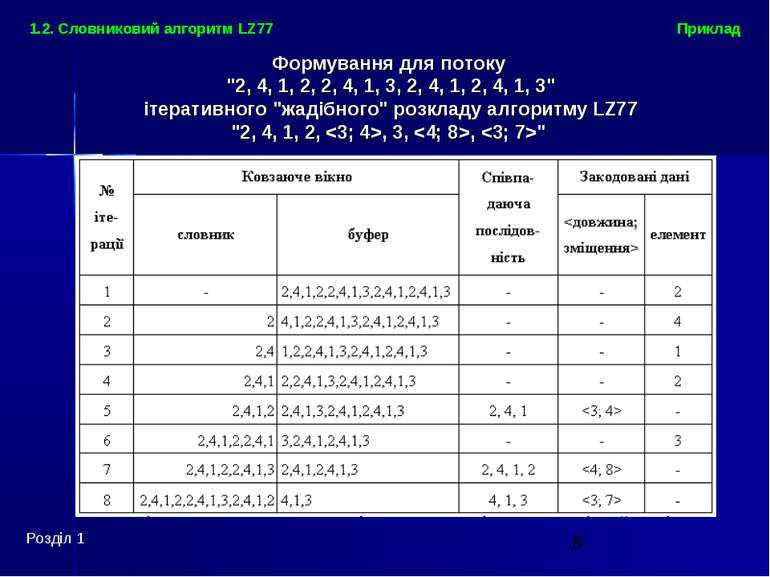
Формування для потоку "2, 4, 1, 2, 2, 4, 1, 3, 2, 4, 1, 2, 4, 1, 3" ітеративного "жадібного" розкладу алгоритму LZ77 "2, 4, 1, 2, , 3, , " Розділ 1 Приклад 1.2. Словниковий алгоритм LZ77

Розділ 1 Теоретичні основи 1.2. Словниковий алгоритм LZ77 Варіанти розкладу алгоритму LZ77, що розглядалися в роботі: “жадібний” розклад; майже оптимальний розклад розклад з “лінивими” порівняннями розклад Кадача , ; ; .

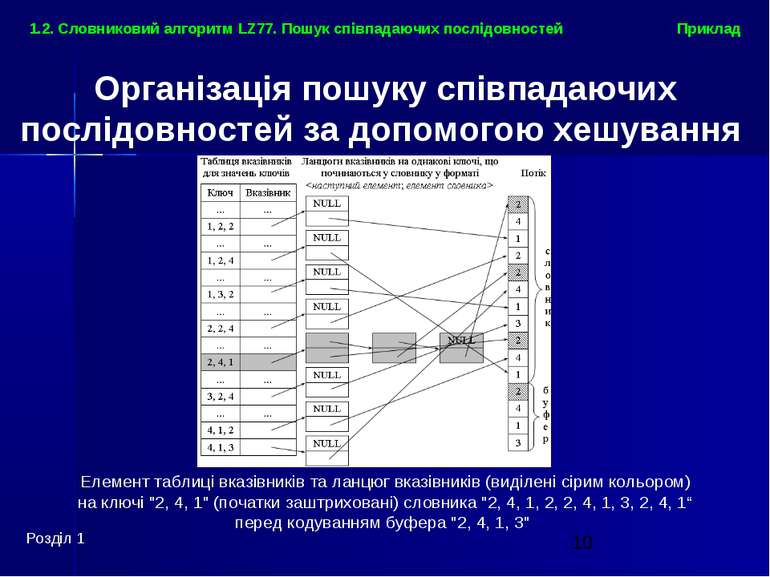
Організація пошуку співпадаючих послідовностей за допомогою хешування Розділ 1 Приклад 1.2. Словниковий алгоритм LZ77. Пошук співпадаючих послідовностей Елемент таблиці вказівників та ланцюг вказівників (виділені сірим кольором) на ключі "2, 4, 1" (початки заштриховані) словника "2, 4, 1, 2, 2, 4, 1, 3, 2, 4, 1“ перед кодуванням буфера "2, 4, 1, 3"

Розділ 1 Приклад 1.2. Словниковий алгоритм LZ77. Пошук співпадаючих послідовностей Елемент хеш-таблиці та хеш-ланцюг вказівників (виділені сірим кольором) на трьохелементні ключі з хеш-значенням "7" (початки заштриховані) хеш-функції сумування кодів трьохелементних ключів

Розділ 1 Теоретичні основи 1.3. Кодування Хафмана та його альтернативи 1. Підраховують ймовірності окремих елементів; 2. Впорядковують елементи за спаданням ймовірностей; 3. Ітеративно поєднують до отримання одного елемента два елементи з найменшими ймовірностями (останні в утвореному списку). При цьому дописують першому з поєднуваних елементів код "0", а другому – "1", сумують ймовірності цих елементів для обчислення ймовірності утвореного елемента та вставляють утворений елемент у відсортований список ймовірностей; 4. Утворюють коди Хафмана, записуючи сформовані коди у зворотному порядку – від вершини до кожного вхідного елемента. Кроки алгоритму генерації динамічних кодів Хафмана: У форматі DEFLATE літерали/базові значення довжин та базові значення зміщень, що утворюються після виконання алгоритму LZ77, кодуються різними кодами Хафмана. Це пов'язано як з неоднаковими діапазонами значень елементів так і з різними характерами нерівномірностей розподілів їх частот.

Розділ 1 Теоретичні основи 1.3. Кодування Хафмана та його альтернативи Обмеження середньої довжини коду Хафмана Згідно з фундаментальним положенням теорії інформації, для мінімізації довжини коду послідовності, елемент si з ймовірністю появи p(si) доцільно кодувати -log p(si) бітами. Тому середня довжина коду елемента блоку після застосування будь-якого контекстно-незалежного алгоритму (у тому числі, і кодування Хафмана), згідно з формулою Шеннона не може бути меншою ентропії джерела Ентропія джерела зменшується зі збільшенням нерівномірності розподілу ймовірностей між елементами. Середня довжина коду Хафмана для різних блоків незначно (в межах біта) перевищує ентропію і досягає цього значення лише у випадку, коли всі -log p(si) цілі числа.

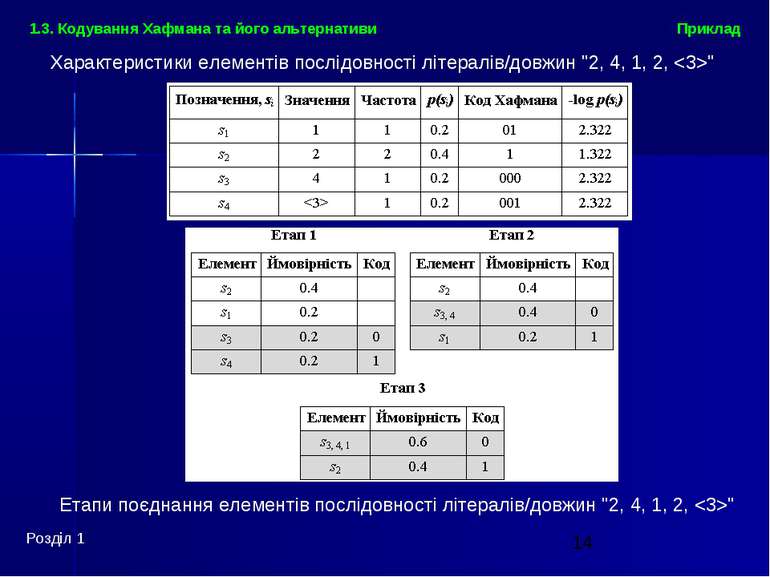
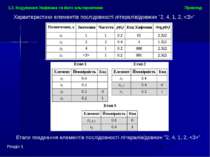
Розділ 1 Приклад 1.3. Кодування Хафмана та його альтернативи Характеристики елементів послідовності літералів/довжин "2, 4, 1, 2, " Етапи поєднання елементів послідовності літералів/довжин "2, 4, 1, 2, "

Розділ 1 Підвищення ефективності 1.3. Кодування Хафмана та його альтернативи Шляхи підвищення ефективності кодування Хафмана, що розглядалися в роботі: розбиття зображення на блоки рядків, результатів розкладу LZ77 – на окремі фрагменти з метою підвищення нерівномірності розподілу ймовірностей між елементами; групове кодування яскравостей компонентів пікселів під час формування палітри (як неявне трикратне розширення джерела, що підпадає під дію першої теореми Шеннона); застосування альтернативного арифметичного кодування зі статичною стратегією формування інтервалів елементів (див. наступний слайд).

Розділ 1 Підвищення ефективності 1.3. Кодування Хафмана та його альтернативи Етапи арифметичного кодування трьох перших елементів послідовності літералів/довжин "2, 4, 1, 2, " Ітеративний принцип арифметичного кодування: Під час чергової ітерації кожному елементу ставиться у відповідність підінтервал з активного інтервалу, що має довжину, пропорційну його ймовірності. Після цього для кодування чергового елемента потоку обирається і надалі розглядається підінтервал, що йому відповідає. Результатом ARIC є довільне число з останнього активного інтервалу.

Результат дії предикторів обчислюється за формулою Теоретичні основи Розділ 1 1.4. Предиктори та їх використання Предиктор – це функція, що намагається, використовуючи значення відомих суміжних елементів, спрогнозувати (змоделювати) значення чергового елемента. Механізм застосування предикторів

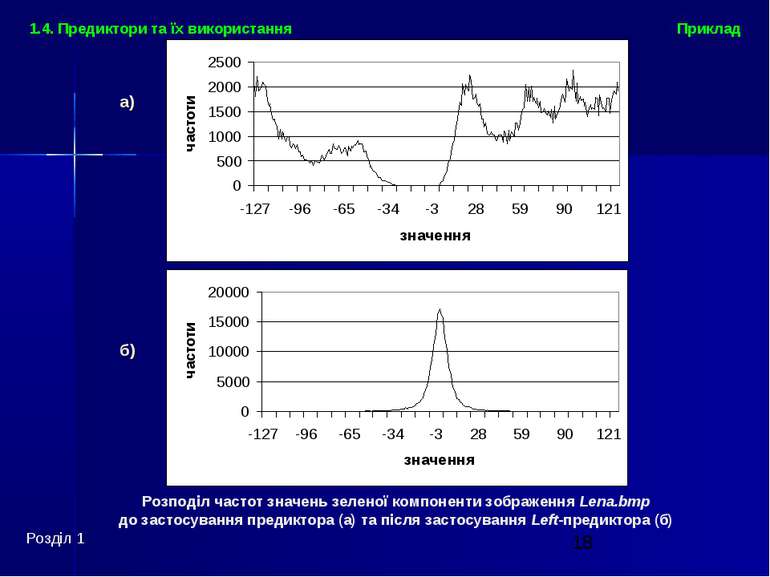
Розподіл частот значень зеленої компоненти зображення Lena.bmp до застосування предиктора (а) та після застосування Left-предиктора (б) а) б) Приклад Розділ 1 1.4. Предиктори та їх використання

Теоретичні основи Розділ 1 1.4. Предиктори та їх використання Предиктори формату PNG Схема розміщення суміжних елементів для елемента Х Предиктори формату PNG мовою C: char NonePredict(char Left, char Above, char LeftAbove) {return 0; } char LeftPredict(char Left, char Above, char LeftAbove) {return Left; } char AbovePredict(char Left, char Above, char LeftAbove) {return Above; } char AveragePredict(char Left, char Above, char LeftAbove) {return (Left+Above)/2; } char PaethPredict(char Left, char Above, char LeftAbove) {int pp=Left+Above-LeftAbove; pa=abs(pp-Left); pb=abs(pp-Above); pc=abs(pp-LeftAbove); if (pa

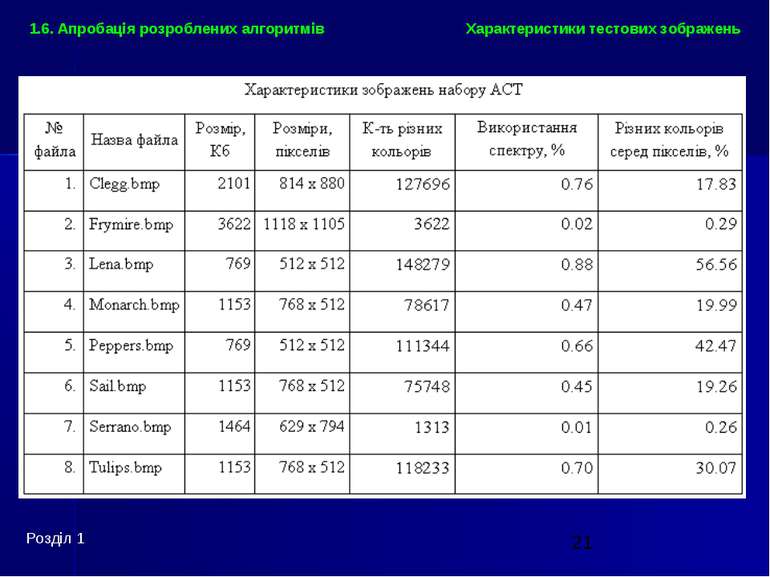
Забезпечення апробації алгоритмів Розділ 1 1.6. Апробація розроблених алгоритмів Тестові набори файлів зображень, апаратне, системне та прикладне програмне забезпечення для апробації розроблених алгоритмів: всі розроблені та описані в роботі алгоритми апробувалися на восьми файлах 24-бітних зображень стандартного набору ACT; остаточні версії програм додатково апробувалися на 24 файлах 24-бітних неперервно-тонових, природних зображень стандартного набору KTCI; тестування розроблених алгоритмів проводилися на комп'ютері з процесором AMD-K6 300 MHz, 128 Mb RAM в операційній системі Windows 98 за допомогою власних програм, розроблених на базі програми з CD для запису зображень у форматі PNG; результати виконання остаточної програми, що реалізує стиснення за допомогою запропонованих алгоритмів в існуючому стандарті PNG порівнювалися з результатами програми OptiPNG, а програми для стиснення в модифікованому стандарті – додатково з програмами WinRAR v. 3.0, JLSEncoder v. 2.2, BMF v. 2.0, ERI v. 5.1.

Характеристики тестових зображень Розділ 1 1.6. Апробація розроблених алгоритмів

Структура Розділ 2 Структура розділу Розділ 2. Прискорення стиснення зображень у форматі PNG 2.1. Вибір найкоротших хеш-ланцюгів у процесі пошуку співпадаючих послідовностей для розкладу алгоритму LZ77 2.2. Способи та алгоритми розрахунків довжин блоків динамічних кодів Хафмана 2.3. Висновки до розділу

Основна ідея алгоритму вибору найкоротших хеш-ланцюгів під час пошуку найдовшої співпадаючої послідовності для розкладу LZ77: подальший пошук найдовшої однакової послідовності у словнику можна виконувати по хеш-ланцюгах довільного ключа, що повністю належить розширеній послідовності буфера. Під час реалізації пошуку врахуємо також, що: переходити до іншого хеш-ланцюга доцільно лише тоді, коли в ньому міститься менше елементів, ніж залишилося розглянути в поточному хеш-ланцюгу; аналізувати розширену послідовність буфера доцільно лише тоді, коли в ній міститься менше неопрацьованих ключів від нерозглянутих елементів в поточному хеш-ланцюгу. Опис алгоритму Розділ 2 2.1. Вибір найкоротших хеш-ланцюгів для розкладу LZ77

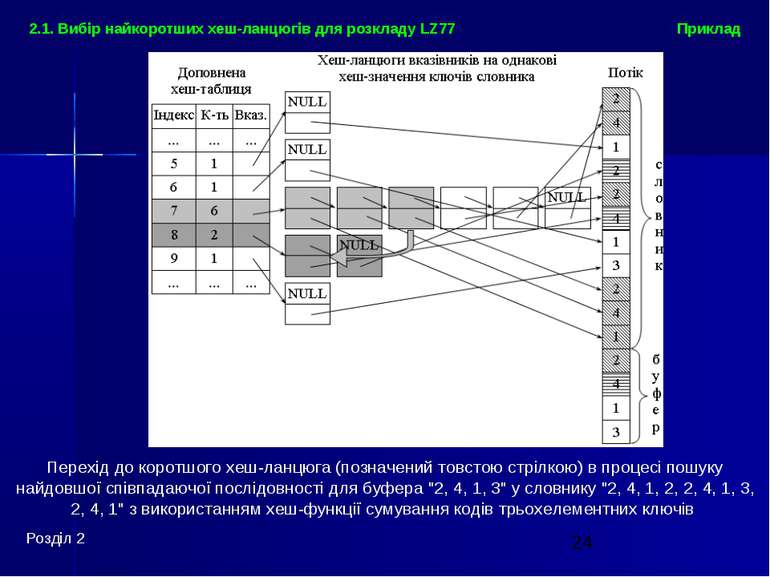
Приклад Розділ 2 2.1. Вибір найкоротших хеш-ланцюгів для розкладу LZ77 Перехід до коротшого хеш-ланцюга (позначений товстою стрілкою) в процесі пошуку найдовшої співпадаючої послідовності для буфера "2, 4, 1, 3" у словнику "2, 4, 1, 2, 2, 4, 1, 3, 2, 4, 1" з використанням хеш-функції сумування кодів трьохелементних ключів

Результати тестування Розділ 2 2.1. Вибір найкоротших хеш-ланцюгів для розкладу LZ77 Основні результати застосування алгоритму вибору найкоротших хеш-ланцюгів у процесі пошуку співпадаючих послідовностей для розкладу алгоритму LZ77: застосування розглянутого алгоритму у випадку відсікання хеш-ланцюгів не лише прискорює виконання стиснення дискретно-тонових зображень на понад 20 %, а й покращує КС окремих файлів на 0.46 % завдяки ефективнішому аналізу послідовностей словника; використання розробленого алгоритму для аналізу всіх елементів хеш-ланцюгів дозволяє прискорити стиснення файлів набору ACT у понад 4.5 рази в основному за рахунок дискретно-тонових зображень; стиснення файлів за допомогою алгоритму вибору найкоротших хеш-ланцюгів по часу майже співпадає зі стисненням файлів за допомогою алгоритму аналізу хеш-ланцюгів згідно ключів початку буфера з відсіканням, але для дискретно-тонових зображень забезпечує відносно нього кращий КС.

Теоретичні основи та результати Розділ 2 2.2. Розрахунки довжин блоків динамічних кодів Хафмана Наближене обчислення довжини блоку кодів Хафмана за допомогою ентропії Основні результати застосування способу наближеного обчислення довжини блоку кодів Хафмана за допомогою ентропії : дає змогу прискорити ці обчислення відносно варіанту безпосередньої генерації для блоків літералів/довжин в середньому на 96.5 %, а для блоків зміщень – на 80.8 %; додатково прискорити такі розрахунки відповідно на 0.37 % і на 0.57 % можливо за допомогою масиву значень двійкових логарифмів для малих (до 15 включно) частот.

Теоретичні основи Розділ 2 2.2. Розрахунки довжин блоків динамічних кодів Хафмана Алгоритм точного обчислення довжини блоку кодів Хафмана: під час чергової ітерації до отримання однієї частоти серед всіх додатних частот знайти дві найменші, збільшити довжину блоку на суму цих частот і надалі замість цих двох частот розглядати їх суму (оскільки внаслідок ітеративного поєднання двох найменших частот у процесі генерації цих кодів довжина блоку збільшується на їх суму). Для точного обчислення довжини блоку кодів Хафмана доцільно: впорядкувати ненульові частоти за спаданням та щоразу, до отримання однієї з них, опрацьовувати дві останні частоти.

Приклад Розділ 2 2.2. Розрахунки довжин блоків динамічних кодів Хафмана Ітеративні поєднання двох найменших частот в процесі точного розрахунку довжини блоку кодів Хафмана Приклад точного обчислення довжини блоку кодів Хафмана

Результати та вдосконалення Розділ 2 2.2. Розрахунки довжин блоків динамічних кодів Хафмана дає змогу прискорити точні розрахунки довжин блоків кодів Хафмана відносно варіанту безпосередньої генерації для блоків літералів/довжин в середньому на 87 %, а для блоків зміщень – на 78 %; застосування однозв'язного списку для уникнення переміщень елементів в процесі вставок сум двох найменших частот дає змогу додатково прискорити ці розрахунки відповідно на 5 % і 4 %, а окреме опрацювання малих частот – ще на 4 % і 3.5 % для таких блоків за рахунок зменшення кількості ненульових частот на 30-40 %. Основні результати застосування алгоритму точного обчислення довжини блоку кодів Хафмана : Приклад окремого опрацювання малих частот в процесі точного розрахунку довжини блоку кодів Хафмана

Структура Розділ 3 Структура розділу Розділ 3. Зменшення коефіцієнтів стиснення RGB-зображень у форматі PNG 3.1. Алгоритм мінімізації розміру стиснутих блоків 3.2. Організація вибору предикторів для рядків пікселів 3.3. Фрагментування зображень 3.4. Мінімізація зміщень результатів розкладу алгоритму LZ77 3.5. Попередній аналіз зображень з розбиттям на мінімальні та однорідні блоки рядків 3.6. Висновки до розділу

Теоретичні основи Розділ 3 3.1.Алгоритм мінімізації розміру стиснутих блоків Основна ідея алгоритму мінімізації розміру стиснутих блоків: зменшити розмір стиснутих блоків динамічних кодів Хафмана у форматі PNG доцільно за рахунок відкидання неефективних замін LZ77, заміщаючи їх відповідними літералами Заміну LZ77 слід вважати ефективною, якщо вона записуються не більшою кількістю бітів, ніж відповідні окремі літерали:

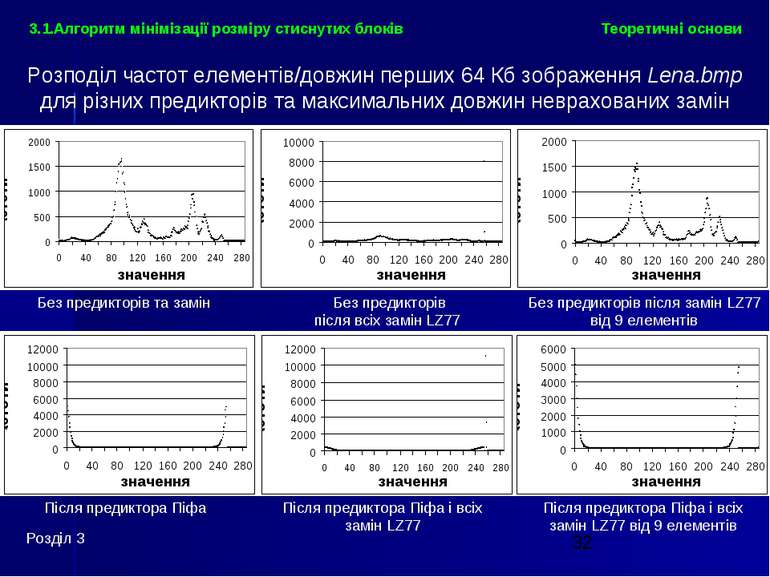
Теоретичні основи Розділ 3 3.1.Алгоритм мінімізації розміру стиснутих блоків Розподіл частот елементів/довжин перших 64 Кб зображення Lena.bmp для різних предикторів та максимальних довжин неврахованих замін Без предикторів та замін Після предиктора Піфа Без предикторів після всіх замін LZ77 Без предикторів після замін LZ77 від 9 елементів Після предиктора Піфа і всіх замін LZ77 Після предиктора Піфа і всіх замін LZ77 від 9 елементів

Теоретичні основи Розділ 3 3.1.Алгоритм мінімізації розміру стиснутих блоків короткі заміни виявляються ефективними, як правило, для стиснутих блоків, у яких інші короткі заміни теж враховуються; короткі заміни виявляються, як правило, неефективними для стиснутих блоків, у яких інші короткі заміни теж не враховуються. За результатами дослідження ефективності замін LZ77 різної довжини встановлено, що:

Теоретичні основи Розділ 3 3.1.Алгоритм мінімізації розміру стиснутих блоків Кроки алгоритму мінімізації розміру кожного стиснутого блоку: створити альтернативні стиснуті блоки з різними максимальними довжинами неврахованих замін; обрати серед них найкоротший блок, використовуючи алгоритми розрахунків довжин динамічних кодів Хафмана з попереднього розділу; ітеративно зменшити його довжину, відкидаючи щоразу неефективні та враховуючи ефективні заміни LZ77; використати сформований блок для зберігання даних у PNG-файлі.

Результати тестування Розділ 3 3.1.Алгоритм мінімізації розміру стиснутих блоків Основні результати застосування алгоритму мінімізації розміру стиснутих блоків: КС неперервно-тонових зображень набору ACT, в яких всі заміни не враховуються зменшився на 2 – 6 %; при цьому час кодування збільшився в середньому на 7 %. Область застосування в дослідженні алгоритму мінімізації розміру стиснутих блоків: всі розроблені алгоритми компресії; всі розроблені алгоритми попереднього аналізу стиснутих блоків.

Результати тестування та висновки Розділ 3 3.2. Організація вибору предикторів для рядків пікселів Основні результати аналізу впливу різних предикторів, алгоритму LZ77 та кодування Хафмана на КС стиснення зображень: для дискретно-тонових фрагментів зображень найменші КС забезпечують предиктори NonePredict, LeftPredict чи RightPredict . Ключову роль в процесі стиснення цих фрагментів відіграє алгоритм LZ77; для неперервно-тонових фрагментів зображень найкращі КС отримуються у випадку застосування AveragePredict чи PaethPredict . Основну роль під час стиснення таких фрагментів виконує кодування Хафмана. розклад LZ77 та кодування Хафмана у поєднанні з алгоритмом мінімізації розмірів стиснутих блоків потрібно застосовувати в процесі стиснення кожного зображення; не існує універсального предиктора, застосування якого сприяло б найкращому стисненню всіх типів зображень. Отже, в процесі стиснення доцільно використовувати різні предиктори для різних рядків. Висновки за результатами застосування різних способів кодування:

Теоретичні основи та висновки Розділ 3 3.2. Організація вибору предикторів для рядків пікселів Розроблені способи вибору предикторів для рядків пікселів: безпосередній ентропійний спосіб; ентропійний спосіб після застосування коротких замін LZ77; комбінований ентропійний спосіб; комбінований ентропійний спосіб з додатковим попіксельним розкладом алгоритмом LZ77 оригіналу зображення; ентропійний спосіб з прогнозуванням результатів розкладів алгоритму LZ77. для кожного рядка зображення найефективнішим може виявитися один з п'яти варіантів компресії: без застосування предикторів, з використанням LeftPredict, з застосуванням RightPredict, з використанням безпосереднього ентропійного способу вибору предикторів та з застосуванням ентропійного способу вибору предикторів після імітації коротких замін LZ77. Висновок за результатами застосування різних способів вибору предикторів:

Теоретичні основи Розділ 3 3.2. Фрагментування зображень зменшення КС кодування Хафмана за рахунок збільшення нерівномірностей розподілів в результаті зміщення меж як між блоками рядків зображення, так і між частинами розкладу LZ77 Мета застосування досліджених алгоритмів фрагментування: Твердження: довжина ентропійного коду (до якої наближається довжина коду Хафмана) поєднання двох послідовностей елементів є не меншою від суми довжин ентропійних кодів цих послідовностей. Залежність приросту довжини ентропійного коду від частот елемента у вхідних послідовностях Висновок: довжина ентропійного коду незначно зростає лише внаслідок поєднання блоків рядків з близькими відносними частотами окремих елементів.

Теоретичні основи та результати Розділ 3 3.2. Фрагментування зображень Досліджені алгоритми фрагментування: розбиття зображень на блоки рядків, що базується на ітеративному поєднанні суміжних блоків з найменшим прогнозованим збільшенням довжини ентропійного коду, доки це збільшення не перевищує середнього розміру заголовка нового стиснутого блоку; розбиття результатів розкладу LZ77 за допомогою методу О. А. Ратушняка на фрагменти з відмінними нерівномірностями розподілів відносних частот елементів. застосування алгоритму розбиття на блоки рядків ефективніше для неперервно-тонових, а фрагментування результатів розкладу LZ77 – для дискретно-тонових зображень, хоча обидва ці алгоритми зменшують КС лише на соті долі процента, що вказує на однорідність результатів дії предикторів та коректність обмеження у програмних реалізаціях максимального розміру блоку стиснутих даних формату DEFLATE 65536 елементами; враховуючи значно вищу швидкість розбиття на блоки рядків стосовно сегментації результатів розкладу LZ77, надалі у дослідження використано саме цей алгоритм фрагментування. Висновки за результатами застосування алгоритмів фрагментування:

Принцип мінімізації зміщень результатів розкладу LZ77 Теоретичні основи Розділ 3 3.4. Мінімізація зміщень результатів розкладу LZ77

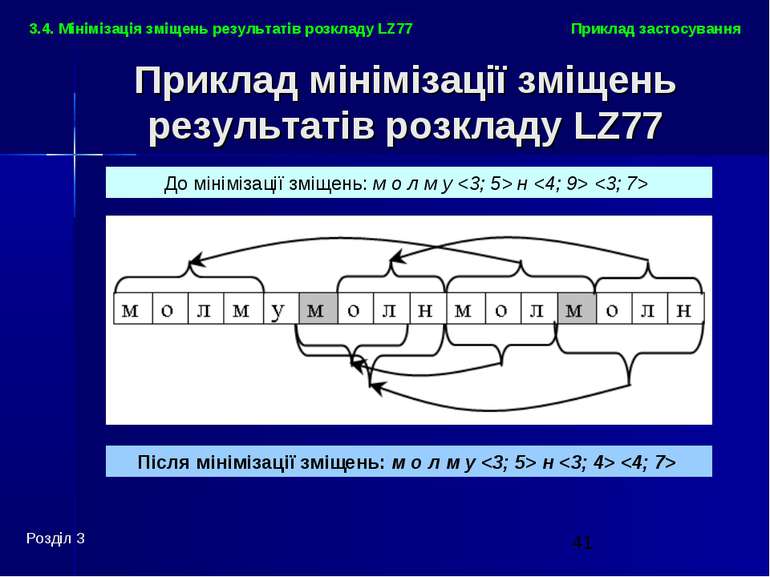
Приклад застосування Розділ 3 3.4. Мінімізація зміщень результатів розкладу LZ77 Приклад мінімізації зміщень результатів розкладу LZ77 Після мінімізації зміщень: м о л м у н До мінімізації зміщень: м о л м у н

застосування даного алгоритму скорочує відставання від результатів програми з майже оптимальним розкладом у середньому на 15 %, сповільнюючи при цьому стиснення в середньому лише на 2.46 %. Результати тестування Розділ 3 3.4. Мінімізація зміщень результатів розкладу LZ77 Основні результати застосування алгоритму мінімізації зміщень результатів розкладу LZ77:

Теоретичні основи Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків розбиття зображень на однорідні блоки та визначення для кожного з них найефективнішого (з п'яти визначених вище) варіанту і параметрів компресії, що забезпечують найменший КС зображення, використовуючи метод динамічного програмування. Призначення алгоритму попереднього аналізу зображень з розбиттям на мінімальні та однорідні блоки рядків: Етапи алгоритму: поєднання суміжних рядків з близькими нерівномірностями розподілів частот елементів в мінімальні блоки (до 32 Кб) і визначення методом динамічного програмування для кожного з них варіанту компресії, що забезпечує загальний мінімальний КС зображення; поєднання суміжних мінімальних блоків рядків з однаковими варіантами компресії та близькими нерівномірностями розподілів частот літералів/довжин в однорідні блоки рядків; розрахунок для кожного з однорідних блоків рядків прогнозованих довжин кодів розподілів літералів/довжин та зміщень з прогнозованих частот розподілів цих блоків або за результатами додаткового “лінивого” розкладу для подальшого формування "лінивого" чи майже оптимального розкладу алгоритму LZ77 в процесі безпосереднього стиснення зображення.

Приклад Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Приклад застосування алгоритму попереднього аналізу зображень з розбиттям на мінімальні та однорідні блоки рядків Межі мінімальних та однорідних блоків рядків тестового зображення

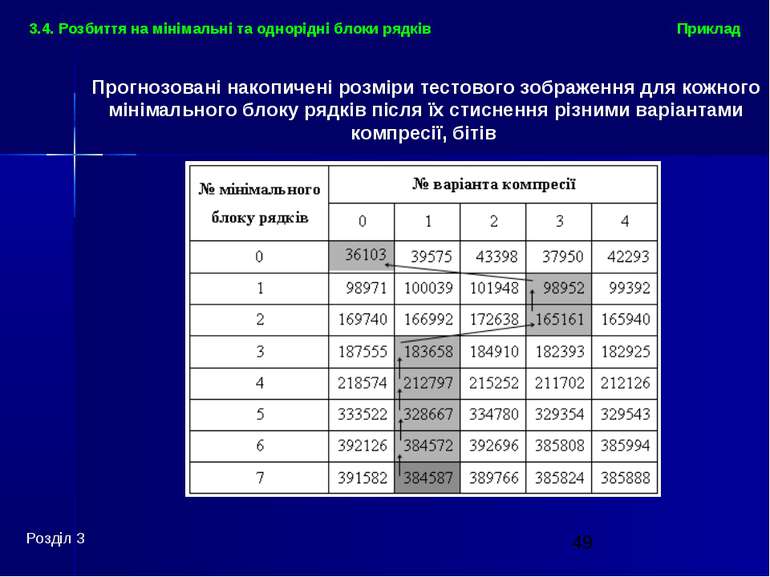
Приклад Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Прогнозовані розміри мінімальних блоків рядків тестового зображення після стиснення різними варіантами компресії, бітів

Теоретичні основи Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Формули для визначення мінімального накопиченого прогнозованого розміру від початку зображення до кожного мінімального блоку рядків i включно за умови застосування до нього варіанта компресії j (прямий хід методу динамічного програмування):

Теоретичні основи Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Штрафи finek,j за відхилення між варіантами компресії суміжних мінімальних блоків, бітів

Теоретичні основи Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Формули для визначення мінімального прогнозованого розміру зображення та оптимальних варіантів компресії кожного мінімального блоку рядків i, що забезпечують цей мінімальний розмір (зворотній хід методу динамічного програмування):

Приклад Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Прогнозовані накопичені розміри тестового зображення для кожного мінімального блоку рядків після їх стиснення різними варіантами компресії, бітів

Теоретичні основи Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Особливості реалізації алгоритму попереднього аналізу зображень з розбиттям на мінімальні та однорідні блоки рядків: уточнити розраховані за частотами елементів для кожного однорідного блоку рядків прогнозовані довжини кодів Хафмана розподілів літералів/довжин замін та зміщень (у випадку відсутності обмежень по часу) можна з розподілів, що утворюються за результатами додаткового проходу по даних зображення з застосуванням обраних предикторів, "лінивого" розкладу LZ77, кодування Хафмана та алгоритму мінімізації розміру стиснутих блоків; визначення прогнозованих розмірів кожного блоку добре піддається розпаралеленню з використанням паралельних процесів для кожного з п'яти варіантів компресії, адже визначення прогнозованого розміру чергового мінімального блоку рядків після застосування кожного варіанту компресії не залежить від інших варіантів компресії. Застосування такого розпаралелення дає змогу підвищити швидкість розрахунку цих розмірів в 4 - 5 разів і, відповідно, прискорити стиснення зображень на 38 - 56 %.

Розділ 3 3.4. Розбиття на мінімальні та однорідні блоки рядків Результати тестування Основні результати застосування алгоритму попереднього аналізу зображень з розбиттям на мінімальні та однорідні блоки рядків: використання даного алгоритму та "лінивого" розкладу LZ77 дає змогу зменшити КС у середньому на 1.58 %, хоча й сповільнює кодування у 4 рази; застосування ж майже оптимального розкладу замість "лінивого" у цій же програмі дозволяє зменшити КС у середньому на 2.92 %, сповільнюючи кодування у 4.9 рази.

Структура Розділ 4 Структура розділу Розділ 4. Модифікації формату PNG для підвищення ефективності стиснення RGB-зображень 4.1. Використання різних ковзаючих вікон для результатів застосування різних предикторів в процесі формування модифікованого розкладу алгоритму LZ77 4.2. Застосування різницевих кольорових моделей для підвищення ефективності використання предикторів в процесі стиснення RGB-зображень 4.3. Використання палітри для групового статистичного кодування RGB-зображень без втрат 4.4. Застосування арифметичного кодування замість кодування Хафмана в процесі стиснення RGB та палітрових зображень 4.5. Аналіз результатів сукупного застосування досліджених модифікацій формату PNG 4.6. Висновки до розділу

Використання альтернативних ковзаючих вікон для формування розкладу LZ77 Опис алгоритму та приклад Розділ 4 4.1. Використання різних ковзаючих вікон для розкладу LZ77 Основна ідея алгоритму LZPR використання різних ковзаючих вікон для різних предикторів в процесі формування розкладу LZ77: пошук найдовшої співпадаючої послідовності доцільно виконувати у альтернативних ковзаючих вікнах (а не в одному) результатів дії всіх предикторів. У випадку виявлення співпадаючої послідовності її кодують трійкою чисел . Якщо ж жоден з предикторів не дає змоги віднайти співпадаючу послідовність, то в закодовані дані заносять відповідний елемент з результатів дії предиктора з найменшою ентропією

Опис алгоритму Розділ 4 4.1. Використання різних ковзаючих вікон для розкладу LZ77 Основна ідея використання алгоритму вибору найкоротших хеш-ланцюгів під час пошуку найдовшої співпадаючої послідовності в альтернативних ковзаючих вікнах: розпочинаючи пошук у наступному словнику, доцільно відразу порівняти кількість елементів хеш-ланцюга, що відповідає ключу початку буфера, з кількістю ключів у послідовності максимальної довжини за результатами пошуку у попередніх ковзаючих вікнах. Якщо перше з цих чисел перевищує друге, то пошук доцільно виконувати по найкоротшому хеш-ланцюгу серед тих, які відповідають ключам послідовності буфера максимальної довжини за результатами пошуку у попередніх ковзаючих вікнах.

Результати тестування Розділ 4 4.1. Використання різних ковзаючих вікон для розкладу LZ77 Основні результати застосування алгоритмів LZPR та вибору найкоротших хеш-ланцюгів під час пошуку найдовшої співпадаючої послідовності в альтернативних ковзаючих вікнах: застосування алгоритму LZPR дало змогу зменшити коефіцієнт стиснення набору ACT на 3.55 % відносно базової програми; врахування максимальної довжини співпадаючої послідовності з попередніх ковзаючих вікон дозволяє додатково прискорити стиснення на 2.9-3.5 %.

Теоретичні основи Розділ 4 4.2. Застосування різницевих кольорових моделей Призначення алгоритму формування та переходу до різницевих кольорових моделей : покращення КС шляхом зменшення ентропії за рахунок міжкомпонентної декореляції для кожного RGB-зображення у форматах, що використовують предиктори. Переходи до різницевих кольорових моделей застосовувалися в процесі стиснення RGB-зображень і раніше, зокрема, у архіваторі WinRar виконується перехід до моделі R-G, G, B-G. Ми ж пропонуємо для кожного зображення формувати таку різницеву кольорову модель, яка дає змогу максимально зменшити ентропію після застосування предикторів. Для форматів графічних файлів найефективнішими виявилися різницеві кольорові моделі з цілими коефіцієнтами.

Теоретичні основи Розділ 4 4.2. Застосування різницевих кольорових моделей Принцип формування різницевої кольорової моделі з цілими коефіцієнтами для кожного RGB-зображення У випадку використання різницевих кольорових моделей з цілими коефіцієнтами необхідно оцінити доцільність заміни значень компоненти Rij різницями Rij-Gij або Rij-Bij, значень Gij – різницями Gij-Rij або Gij-Bij та значень Bij – різницями Bij-Rij або Bij-Gij, враховуючи використання предикторів. Нехай в межах кожного піксела компонента R має індекс 0, G – 1, B – 2. Запишемо досліджувані ентропійні довжини у вигляді матриці A: Для забезпечення однозначності декодування різницева кольорова модель визначається щонайбільше двома недіагональними елементами різних рядків матриці A, які серед елементів, менших за діагональні елементи своїх рядків, сумарно найбільше від них відхиляються (забезпечують максимальні зменшення ентропійних довжин кодів).

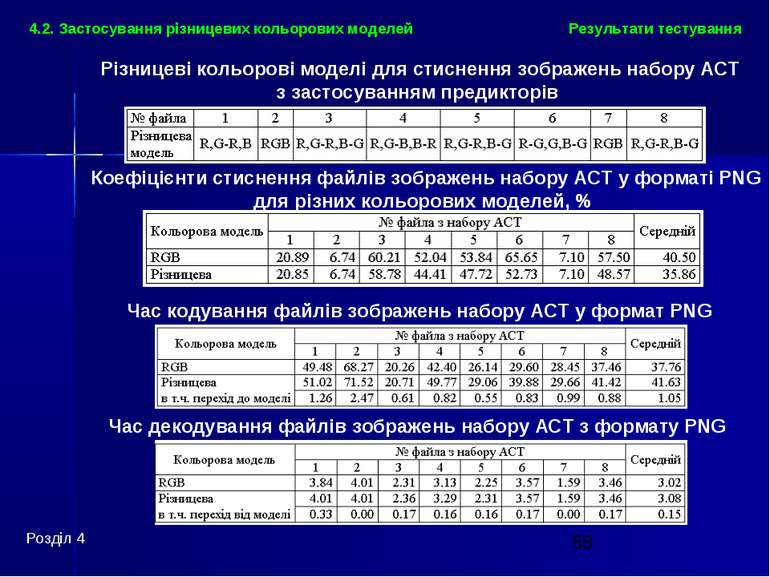
Результати тестування Розділ 4 4.2. Застосування різницевих кольорових моделей Різницеві кольорові моделі для стиснення зображень набору ACT з застосуванням предикторів Коефіцієнти стиснення файлів зображень набору ACT у форматі PNG для різних кольорових моделей, % Час кодування файлів зображень набору ACT у формат PNG Час декодування файлів зображень набору ACT з формату PNG

Результати тестування Розділ 4 4.2. Застосування різницевих кольорових моделей Основні результати застосування алгоритму формування та переходу до різницевих кольорових моделей : використання різницевих кольорових моделей, розрахованих для кожного зображення за даним алгоритмом, дає змогу зменшити КС в середньому на 4.5 % (максимально – на понад 12 %) за рахунок неперервно-тонових зображень. Для цих зображень КС внаслідок застосування різницевих кольорових моделей зменшується зі зменшенням % унікальних кольорів; застосування даних різницевих кольорових моделей дає змогу додатково зменшити КС алгоритму коригування значень предикторів для неперервно-тонових зображень в середньому на 0.74 %, сповільнивши при цьому кодування на 1.64 %. Таке додаткове покращення КС пояснюється зменшенням енергії по двох перетворених компонентах різницевої кольорової моделі.

Теоретичні основи Розділ 4 4.3. Використання палітри для групового кодування Кроки алгоритму перетворення яскравостей кольорів пікселів з метою використання палітри для групового статистичного кодування: Згрупувати кольори пікселів по паралелепіпедах, що не перетинаються: 1.1.  Виконати швидке початкове розбиття простору кольорів RGB на паралелепіпеди, що не перетинаються; 1.2.  Поділити отримані паралелепіпеди так, щоб мінімізувати КС. Зберегти в палітрі найменші значення компонент пікселів, що належать кожному з утворених паралелепіпедів та їх розміри по кожній осі; Подати значення кольору кожного піксела у вигляді індекса в палітрі паралелепіпеда, якому він належить, та зміщення по кожній координаті у середині паралелепіпеда.

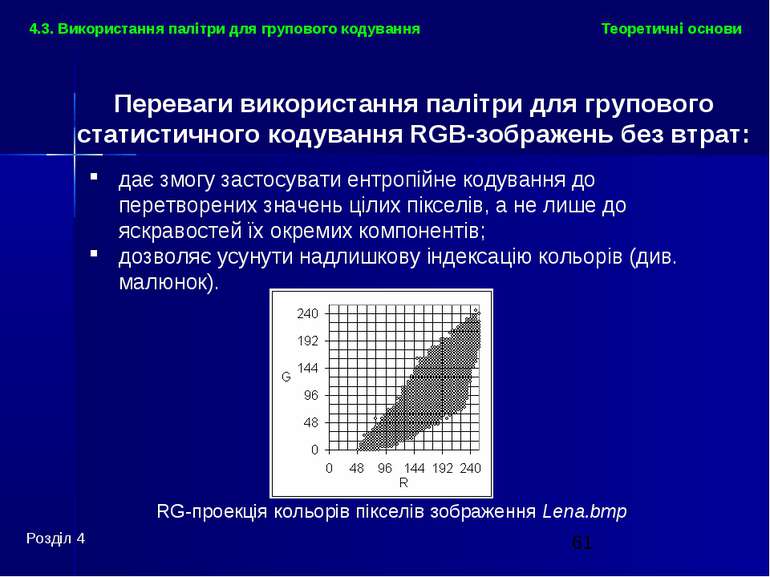
Теоретичні основи Розділ 4 4.3. Використання палітри для групового кодування Переваги використання палітри для групового статистичного кодування RGB-зображень без втрат: дає змогу застосувати ентропійне кодування до перетворених значень цілих пікселів, а не лише до яскравостей їх окремих компонентів; дозволяє усунути надлишкову індексацію кольорів (див. малюнок). RG-проекція кольорів пікселів зображення Lena.bmp

1.1.1. Розбити множину допустимих значень кольорів на паралелепіпеди максимального фіксованого розміру, що не перетинаються між собою, повністю покривають множину допустимих значень кольорової моделі, а їх кількість не перевищує максимально допустимої кількості кольорів палітри; 1.1.2. Визначити кількість кольорів пікселів та межі їх знаходження у кожному паралелепіпеді. Звузити межі кожного паралелепіпеда до меж знаходження кольорів пікселів у ньому; 1.1.3. Поєднати між собою сусідні паралелепіпеди, якщо їх сукупний розмір не перевищує максимального фіксованого; 1.1.4. Зберегти в палітрі координати та розмірності лише тих паралелепіпедів, що містять кольори пікселів зображення. Теоретичні основи Розділ 4 4.3. Використання палітри для групового кодування 1.1. Кроки алгоритму початкового розбиття простору кольорів RGB на паралелепіпеди, що не перетинаються:

Приклад Розділ 4 4.3. Використання палітри для групового кодування Приклад початкового розбиття простору кольорів RGB для умовного зображення на паралелепіпеди, що не перетинаються:

Теоретичні основи Розділ 4ё 4.3. Використання палітри для групового кодування 1.2. Розбиття довільного паралелепіпеда призводить до: зменшення довжини рівномірного коду, враховуючи зменшення розмірів утворених паралелепіпедів по осі поділу (див. рис.); збільшення довжини ентропійного коду внаслідок утворення нового значення в палітрі. RG-проекція зміщень кольорів пікселів умовного кубу

Теоретичні основи Розділ 4 4.3. Використання палітри для групового кодування 1.2. Ітеративний принцип розбиття паралелепіпедів в процесі розширення палітри: під час кожної ітерації визначається паралелепіпед і площина, розбиття якою дає змогу досягнути максимального зменшення довжини групового коду. Наприклад, зміна довжини групового коду внаслідок поділу чергового паралелепіпеда по значенню i осі R обчислюється за формулою:

використання палітри після контекстно-залежного алгоритму LZPR хоча й у середньому сповільнює кодування на 15 %, але прискорює декодування на 6 % та зменшує КС на 1.77 %. Результати тестування Розділ 4 4.3. Використання палітри для групового кодування Основні результати застосування алгоритму палітрування для групового статистичного кодування RGB-зображень без втрат:

Особливості реалізації Розділ 4 4.4. Застосування ARIC замість кодування Хафмана Особливості реалізації арифметичного кодування зі статичною стратегією формування інтервалів елементів: Для реалізації ARIC ми модифікували та застосували range-кодер Е. Шелвіна, оскільки він виконує зчитування/запис байт а не біт даних і за рахунок цього значно прискорює виконання алгоритму кодування/декодування; з метою зберігання довжини інтервалу для кожного елемента у заголовку блоку стиснутих даних замість довжини коду Хафмана нами записується кількість бітів для зберігання відповідної довжини інтервалу в загальному інтервалі [0; 32767), а після заголовка – двійковий запис цієї довжини без першого біта (який завжди рівний одиниці); для прискорення декодування використано байтовий масив, у якому для кожного значення загального інтервалу зберігається номер елемента, що йому відповідає. Застосування такого масиву дає змогу прискорити декодування у середньому на 46 %.

Результати тестування Розділ 4 4.4. Застосування ARIC замість кодування Хафмана у випадку невикористання предикторів КС зображень набору АСТ зменшився максимум на 0.43 %, а в середньому по набору – на 0.1 %. При цьому час кодування скоротився в середньому на 4.85 %, а декодування – на 20 %; застосовуючи предиктори до тих самих зображень, КС зменшився максимум на 0.26 %, а в середньому по набору – на 0.06 %; час кодування зменшився на 1.76 %, а декодування – на 10 %; використання арифметичного кодування після застосування контекстно-залежного алгоритму LZPR та алгоритму палітрування зменшує КС лише на 0.02 %, що вказує на доцільність застосування останнього з цих алгоритмів у форматах для стиснення трикомпонентних зображень кодами Хафмана. Основні результати застосування арифметичного кодування зі статичною стратегією формування інтервалів елементів замість кодування Хафмана:

Результати дослідження Висновки Вирішена науково-практична задача В дисертації сформульована і вирішена актуальна науково-практична задача підвищення ефективності стиснення без втрат у растрових графічних форматах, що використовують предиктори, словниковий алгоритм LZ77, контекстно-незалежне кодування та їх комбінування (зокрема, і в форматі PNG) шляхом врахування взаємодії цих способів кодування та створення нових методів і алгоритмів попередньої обробки зображень. Висновки

1. Вперше розроблено спосіб вибору найкоротших хеш-ланцюгів для прискорення пошуку співпадаючих послідовностей потоку; 2. Вперше запропоновано і реалізовано метод зменшення розміру стиснутого блоку у форматі DEFLATE за допомогою відкидання неефективних замін; 3. Вперше запропоновано і досліджено спосіб розбиття зображення на блоки однорідних рядків для збільшення в них кодової надлишковості та спосіб визначення предикторів рядків за допомогою ентропії; 4. Вперше розроблено метод попереднього аналізу зображень з розбиттям на мінімальні та однорідні блоки рядків з метою визначення для кожного з них оптимального способу кодування; 5. Вдосконалено механізм формування "лінивого" та майже оптимального розкладів методу словникового алгоритму LZ77 з використанням результатів попереднього аналізу зображень; Результати дослідження Висновки Наукові і практичні результати Основні наукові і практичні результати дослідження (початок):

Основні наукові і практичні результати дослідження (продовження): 6. Отримав подальший розвиток метод групового статистичного кодування за допомогою використання палітри в процесі стиснення RGB-зображень без втрат; 7. Вперше розроблено ряд методів для генерування різницевих кольорових моделей як з цілими, так і з дійсними коефіцієнтами, які дають змогу зменшити КС зображень у форматах без втрат, що використовують предиктори, коригування значень предикторів та контекстно-незалежне кодування; 8. Розроблені методи і алгоритми підвищення ефективності стиснення у форматі PNG реалізовані в комп'ютерному комплексі, який дає змогу зменшити КС більшості зображень, стиснутих швидким способом у цьому форматі, на понад 5 %, зокрема, для набору АСТ – у середньому на 5.91 % і досягає по цьому показнику кращих результатів від спорідненого програмного забезпечення; 9. Досліджені методи і алгоритми підвищення ефективності стиснення у форматі PNG шляхом його модифікацій дають змогу зменшити КС більшості зображень, стиснутих швидким способом у цьому форматі, на понад 9 %, зокрема, для набору АСТ – у середньому на 9.86 %. Результати дослідження Висновки Наукові і практичні результати

Дякуємо за увагу!

Дослідження за напрямками паспорту спеціальності 01.05.05 - математичне та програмне забезпечення обчислювальних машин і систем: методи організації ефективних обчислень у комп’ютерних системах; прикладні програмні системи. Підвищення ефективності стиснення RGB-зображень у форматі PNG