Презентація на тему:
Елементарні структури даних: Стеки, черги. Математичні основи аналізу алгоритмів. Графи. Дерева інформації

Алгоритми та структури даних Лекція 3 Елементарні структури даних: Стеки, черги. Математичні основи аналізу алгоритмів. Графи. Дерева. доц. Лавренюк А.М.

Елементарні структури даних: Стеки, черги Стеки та черги — це динамічні множини, елементи з яких видаляються за допомогою попередньо визначеної операції Delete. Першим зі стеку (stack) видаляється елемент, який був поміщений туди останнім: в стеку реалізується стратегія «останнім зайшов — першим вийшов" (last-in, first-out — LIFO). В черзі (queue) завжди видаляється елемент, який міститься в множині довше за інших: в черзі реалізується стратегія «першим зайшов - першим вийшов" (first-in, first-out — FIFO). Реалізуємо обидві ці структури даних за допомогою звичайного масиву.

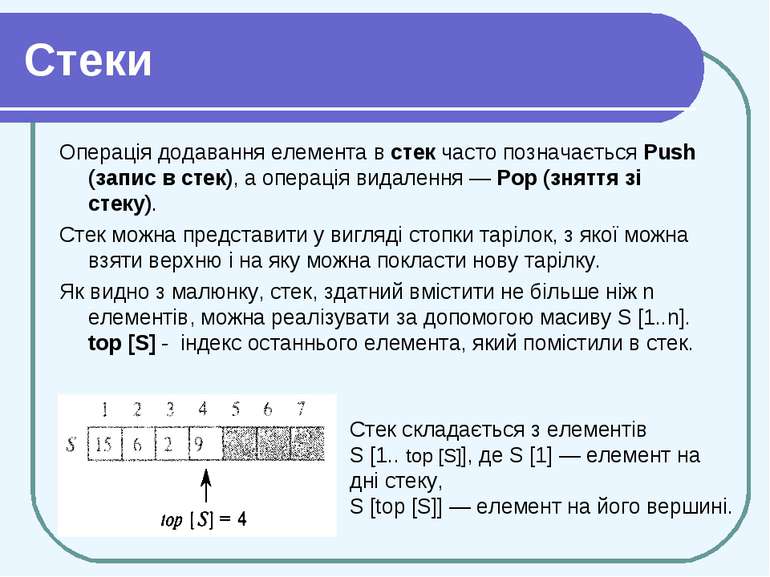
Стеки Операція додавання елемента в стек часто позначається Push (запис в стек), а операція видалення — Pop (зняття зі стеку). Стек можна представити у вигляді стопки тарілок, з якої можна взяти верхню і на яку можна покласти нову тарілку. Як видно з малюнку, стек, здатний вмістити не більше ніж n елементів, можна реалізувати за допомогою масиву S [1..n]. top [S] - індекс останнього елемента, який помістили в стек. Стек складається з елементів S [1.. top [S]], де S [1] — елемент на дні стеку, S [top [S]] — елемент на його вершині.

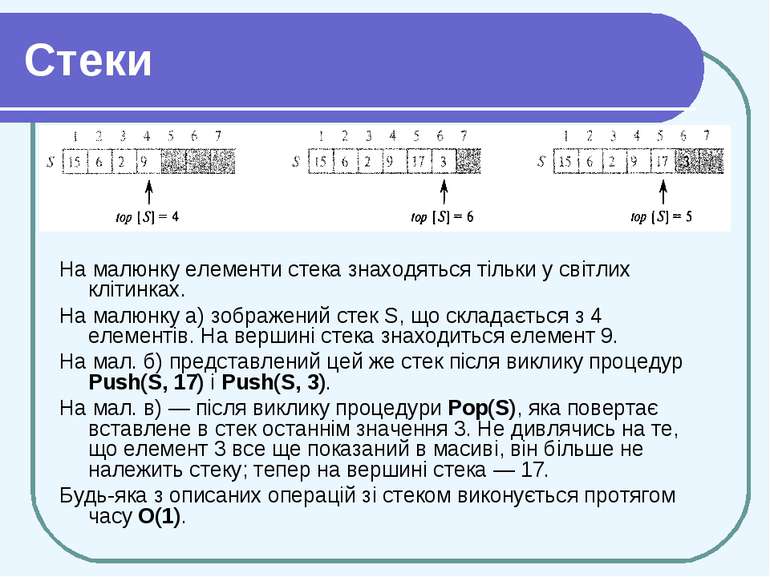
Стеки На малюнку елементи стека знаходяться тільки у світлих клітинках. На малюнку а) зображений стек S, що складається з 4 елементів. На вершині стека знаходиться елемент 9. На мал. б) представлений цей же стек після виклику процедур Push(S, 17) і Push(S, 3). На мал. в) — після виклику процедури Pop(S), яка повертає вставлене в стек останнім значення 3. Не дивлячись на те, що елемент 3 все ще показаний в масиві, він більше не належить стеку; тепер на вершині стека — 17. Будь-яка з описаних операцій зі стеком виконується протягом часу О(1).

Стеки Якщо top [S] = 0, то стек не містить жодного елементу і є пустим (empty). Протестувати стек на наявність в ньому елементів можна за допомогою операції-запиту Stack_Empty. Якщо елемент знімається з пустого стеку, то говорять, що він спустошується (underflow), що зазвичай призводить до помилки. Якщо значення top [S] більше n, то стек переповнюється (overflow). (В представленому нижче псевдокоді можливе переповнення до уваги не береться.)

Стеки Операції зі стеком (перевірка на порожність, додавання елемента, видалення елемента) записуються так: Stack_Empty(S) 1 if top[S]=0 2 then return TRUE 3 else return FALSE Push(S, x) 1 top[S]

Стеки Pop(S) 1 if Stack_Empty(S) 2 then error “underflow” 3 else top[S]

Черги Операцію додавання елемента до черги будемо називати Enqueue (помістити в чергу), а операцію видалення елемента — Dequeue (вивести з черги). Подібно стековій операції Pop, операція Dequeue не потребує передачі елемента масиву, який необхідно видалити, у вигляді аргументу. Він визначений однозначно. Завдяки властивості FIFO черга схожа, наприклад, на живу чергу до лікаря в поліклініці. У неї є голова (head) і хвіст (tail). Коли елемент ставиться в чергу, він займає місце в її хвості, точно так само, як людина займає чергу останньою, щоб потрапити на прийом до лікаря. З черги завжди виводиться елемент, який знаходиться в її головній частині аналогічно тому, як в кабінет лікаря завжди заходить хворий, який чекав довше всіх.

Черги На малюнку черга реалізована за допомогою масиву Q [1..12]. Покажемо, як за допомогою масиву Q [1..n] можна реалізувати чергу, що складається не більше ніж з n-1 елементів. head [Q] - індекс головного елемента або вказівник на нього; tail [Q] – індексує місцезнаходження, куди буде добавлено новий елемент. Елементи черги знаходяться у клітинках head [Q], head [Q] +1,..., tail [Q] -1, які циклічно замкнені (клітинка 1 слідує відразу ж після клітинки n в циклічному порядку).

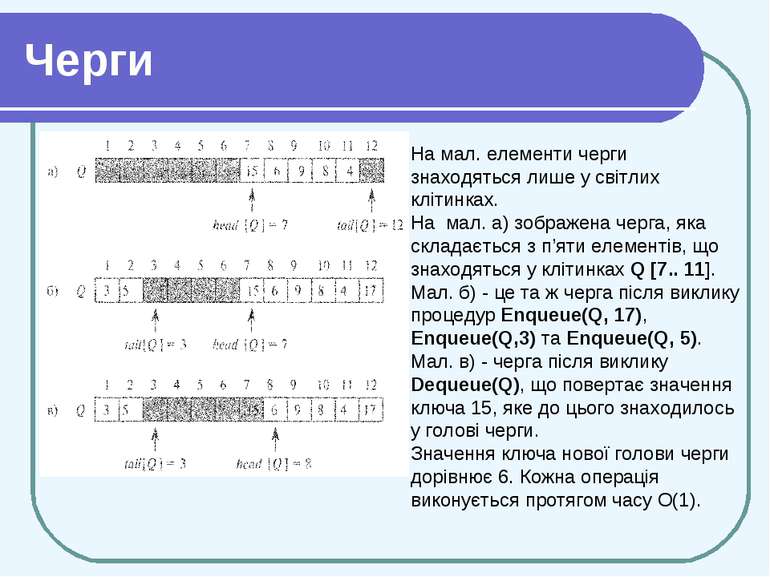
Черги На мал. елементи черги знаходяться лише у світлих клітинках. На мал. а) зображена черга, яка складається з п’яти елементів, що знаходяться у клітинках Q [7.. 11]. Мал. б) - це та ж черга після виклику процедур Enqueue(Q, 17), Enqueue(Q,3) та Enqueue(Q, 5). Мал. в) - черга після виклику Dequeue(Q), що повертає значення ключа 15, яке до цього знаходилось у голові черги. Значення ключа нової голови черги дорівнює 6. Кожна операція виконується протягом часу О(1).

Черги При виконанні умови head [Q] = tail [Q] черга порожня (т.к. за доп. масиву Q [1..n] можна реалізувати чергу, що складається не більше ніж з n-1 елементів). З самого початку виконується співвідношення head [Q] = tail [Q]= 1. Якщо черга порожня, то при спробі видалити з неї елемент відбувається помилка спустошення. Якщо head [Q] = tail [Q]+1, то черга заповнена, і спроба додати до неї елемент призводить до її переповнення (один елем. масиву лишається не заповненим). В наведених нижче процедурах Enqueue та Dequeue перевірка помилок спустошення та переповнення не виконується.

Черги Enqueue(Q,x) 1 Q[tail[Q]]

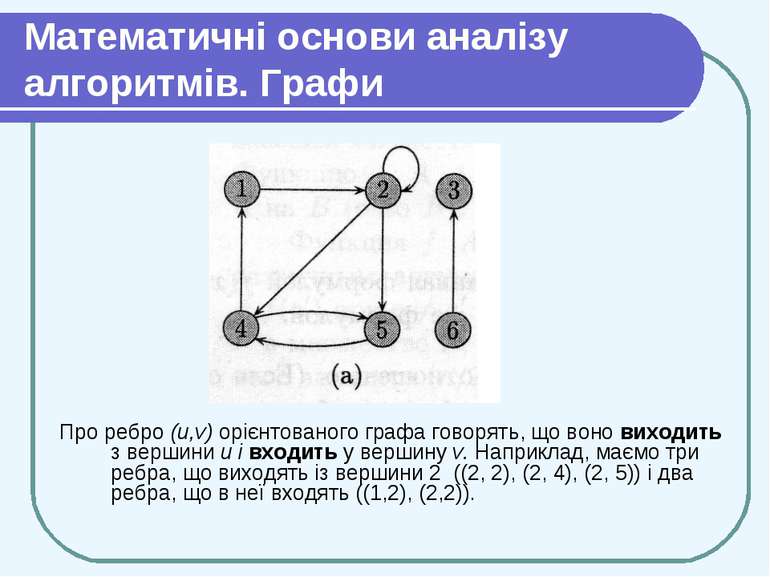
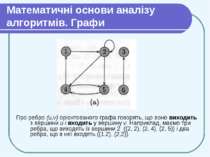
Математичні основи аналізу алгоритмів. Графи. Орієнтований граф (directed graph) визначається як пара (V,E), де V — скінченна множина, а Е — бінарне відношення на V, тобто підмножина множини V х V. Орієнтований граф іноді для скорочення називають орграфом (digraph). Множину V називають множиною вершин графа (vertex set); її елемент називають вершиною графа (vertex, vertices). Множину Е називають множиною ребер (edge set) графа; її елементи називають ребрами (edges). На малюнку (а) показаний орієнтований граф с множиною вершин {1, 2, 3, 4, 5, 6}. Вершини зображені кружками, а ребра — стрілками. Граф може мати ребра-цикли (self-loops), що з’єднують вершину з собою. Орієнтований граф, що не має ребер-циклів, називається простим (simple).

Математичні основи аналізу алгоритмів. Графи Про ребро (u,v) орієнтованого графа говорять, що воно виходить з вершини и і входить у вершину v. Наприклад, маємо три ребра, що виходять із вершини 2 ((2, 2), (2, 4), (2, 5)) і два ребра, що в неї входять ((1,2), (2,2)).

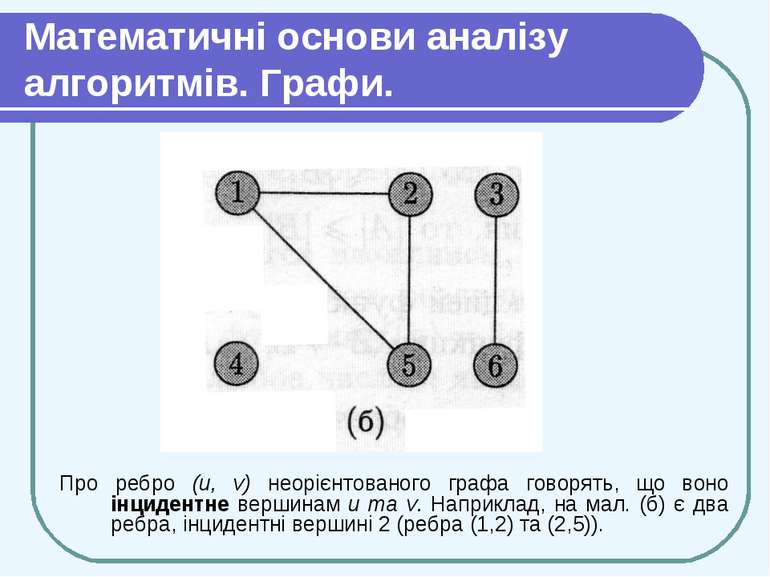
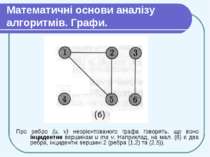
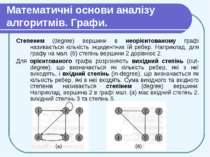
Математичні основи аналізу алгоритмів. Графи. Дерева В неорієнтованому (undirected) графі G = (V, Е) множина ребер Е складається з невпорядкованих (unordered) пар вершин: парами є множини {u,v}, де и, v V і и ≠ v. Для неорієнтованого графа (и, v) і (v, и) позначають одне і те ж ребро. Неорієнтований граф не може містити ребер-циклів, і кожне ребро складається з двох різних вершин («з’єднуючи» їх). На мал. (б) зображено неорієнтований граф с множиною вершин {1,2,3,4,5,6}.

Математичні основи аналізу алгоритмів. Графи. Про ребро (и, v) неорієнтованого графа говорять, що воно інцидентне вершинам и та v. Наприклад, на мал. (б) є два ребра, інцидентні вершині 2 (ребра (1,2) та (2,5)).

Математичні основи аналізу алгоритмів. Графи. Якщо в графі G є ребро (и, v), говорять, що вершина v суміжна з вершиною и. Для неорієнтованих графів відношення суміжності є симетричним. Для орієнтованих графів це не обов’язково. Якщо вершина v суміжна з вершиною и в орієнтованому графі, пишуть и —> v. Для обох малюнків (а) та (б) вершина 2 є суміжною з вершиною 1, але лише на другому з них вершина 1 суміжна с вершиною 2 (в першому випадку ребро (2,1) відсутнє в графі).

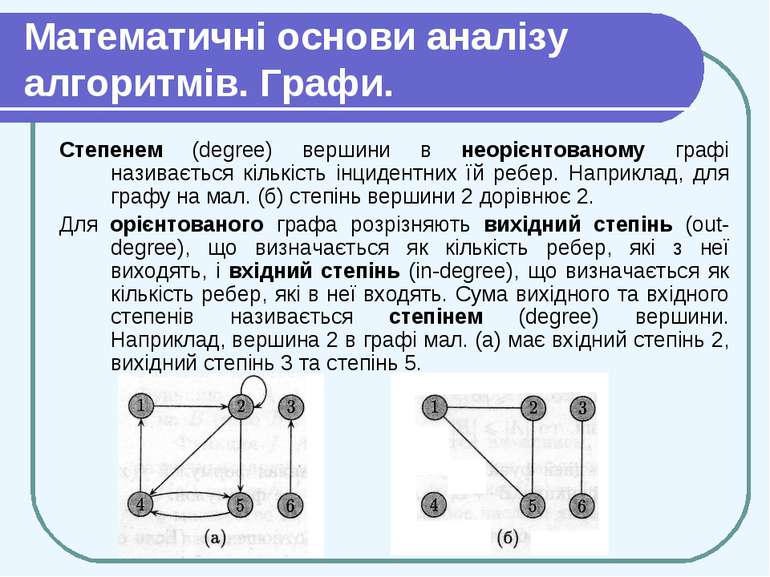
Математичні основи аналізу алгоритмів. Графи. Степенем (degree) вершини в неорієнтованому графі називається кількість інцидентних їй ребер. Наприклад, для графу на мал. (б) степінь вершини 2 дорівнює 2. Для орієнтованого графа розрізняють вихідний степінь (out-degree), що визначається як кількість ребер, які з неї виходять, і вхідний степінь (in-degree), що визначається як кількість ребер, які в неї входять. Сума вихідного та вхідного степенів називається степінем (degree) вершини. Наприклад, вершина 2 в графі мал. (а) має вхідний степінь 2, вихідний степінь 3 та степінь 5.

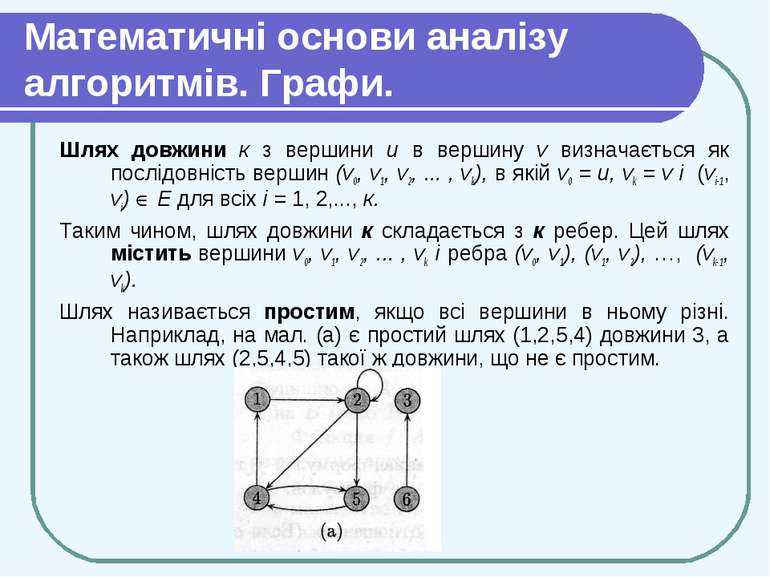
Математичні основи аналізу алгоритмів. Графи. Шлях довжини к з вершини и в вершину v визначається як послідовність вершин (v0, v1, v2, ... , vk), в якій v0 = и, vk = v і (vi-1, vi) Е для всіх i = 1, 2,..., к. Таким чином, шлях довжини к складається з к ребер. Цей шлях містить вершини v0, v1, v2, ... , vk і ребра (v0, v1), (v1, v2), …, (vk-1, vk). Шлях називається простим, якщо всі вершини в ньому різні. Наприклад, на мал. (а) є простий шлях (1,2,5,4) довжини 3, а також шлях (2,5,4,5) такої ж довжини, що не є простим.

Математичні основи аналізу алгоритмів. Графи. Циклом в орієнтованому графі називається шлях, в якому початкова вершина співпадає з кінцевою і який містить хоча б одне ребро. Цикл (v0, v1, v2, ... , vk) називається простим, якщо в ньому немає однакових вершин (окрім першої та останньої), тобто якщо всі вершини v1, v2, ... , vk різні. Ребро-цикл є циклом довжини 1. Будемо ототожнювати цикли, які відрізняються здвигом вздовж циклу: один і той же цикл довжини к може бути представлений к різними шляхами (в якості початку і кінця можна взяти будь-яку з к вершин). Наприклад, на мал. (а) шляхи (1, 2, 4, 1), (2, 4, 1, 2) і (4, 1, 2, 4) є одним і тим же циклом. Цей цикл є простим, тоді як цикл (1,2,4,5,4,1) таким не є. На тому ж малюнку є цикл (2,2), утворений єдиним ребром-циклом (2,2).

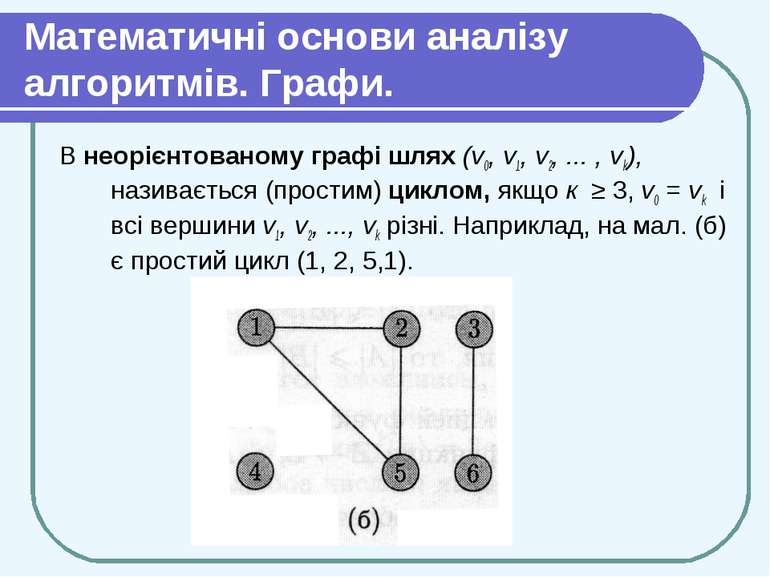
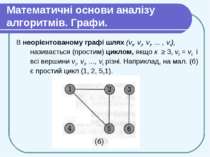
Математичні основи аналізу алгоритмів. Графи. В неорієнтованому графі шлях (v0, v1, v2, ... , vk), називається (простим) циклом, якщо к ≥ 3, v0 = vk і всі вершини v1, v2, ..., vk різні. Наприклад, на мал. (б) є простий цикл (1, 2, 5,1).

Математичні основи аналізу алгоритмів. Графи. Граф, в якому немає циклів, називається ациклічним (acyclic). Неорієнтований граф називається зв’язним, якщо для будь-якої пари вершин існує шлях з однієї в іншу. Деякі види графів мають спеціальні назви. Повним (complete) графом називають неорієнтований граф, що містить всі можливі ребра для даної множини вершин (будь-яка вершина суміжна з будь-якою іншою). Неорієнтований граф (V, Е) називають дводольний (bipartite), якщо множину вершин V можна розбити на дві частини V1 і V2 таким чином, що кінці будь-якого ребра виявляються в різних частинах. Ациклічний неорієнтований граф називають лісом (forest). Зв’язний ациклічний неорієнтований граф називають деревом без виділеного кореня.

Математичні основи аналізу алгоритмів. Дерева. Дерева без виділеного кореня Зв’язним ациклічний неорієнтований граф називають деревом без виділеного кореня. Якщо неорієнтований граф є ациклічним, але незв’язним, його називають лісом (forest); ліс складається з дерев ( що є його зв’язними компонентами).

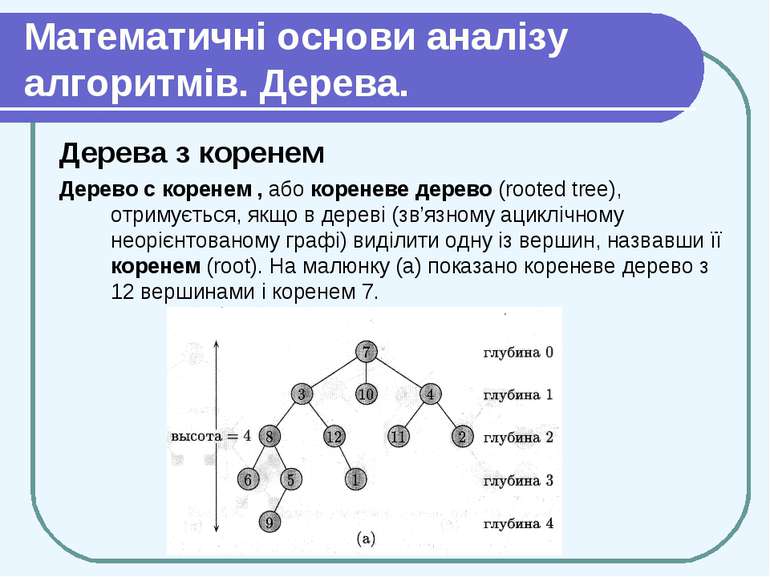
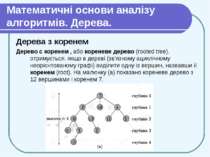
Математичні основи аналізу алгоритмів. Дерева. Дерева з коренем Дерево с коренем , або кореневе дерево (rooted tree), отримується, якщо в дереві (зв’язному ациклічному неорієнтованому графі) виділити одну із вершин, назвавши її коренем (root). На малюнку (а) показано кореневе дерево з 12 вершинами і коренем 7.

Математичні основи аналізу алгоритмів. Дерева. Дерева з коренем Нехай x — будь-яка вершина кореневого дерева з коренем r. Існує єдиний шлях із r в x; всі вершини, що знаходяться на цьому шляху, називаються предками вершини x. Якщо у є предком x, то x називається потомком у. Якщо (у, x) — останнє ребро на шляху з кореня в x, то у називається батьком x, а x називається дитиною у. Корінь є єдиною вершиною, у якої немає батька. Вершини, що мають спільного батька, будемо називати братами. Вершина кореневого дерева, яка не має дітей, називається листком. Вершини, що мають дітей, називаються внутрішніми (internal).

Математичні основи аналізу алгоритмів. Дерева. Дерева с коренем Кількість дітей у вершини кореневого дерева називається її степенем. Для всіх вершин, окрім кореня, степінь на одиницю менше степеня тієї ж вершини в тому ж дереві, якщо розглядати дерево як неорієнтований граф (оскільки тоді потрібно враховувати і ребро, що йде вверх). Довжина шляху від кореня до будь-якої вершини x називається глибиною вершини x. Максимальна глибина вершин дерева називається висотою дерева.

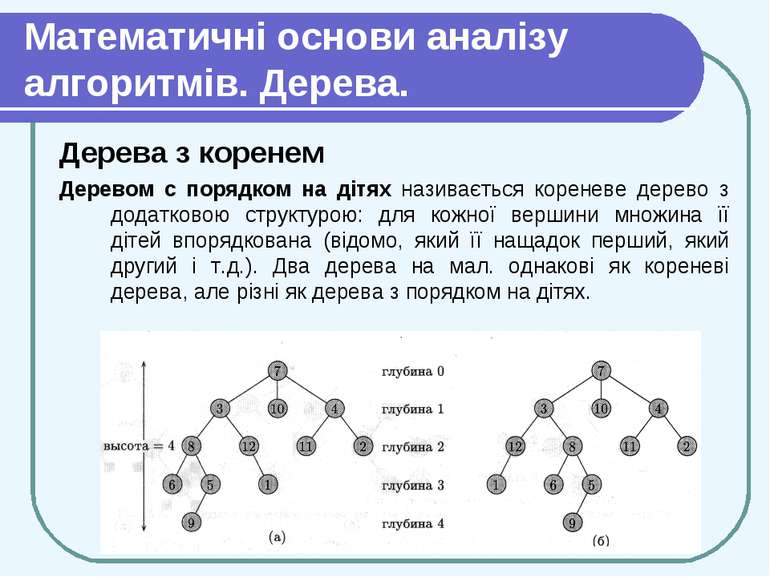
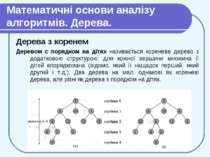
Математичні основи аналізу алгоритмів. Дерева. Дерева з коренем Деревом с порядком на дітях називається кореневе дерево з додатковою структурою: для кожної вершини множина її дітей впорядкована (відомо, який її нащадок перший, який другий і т.д.). Два дерева на мал. однакові як кореневі дерева, але різні як дерева з порядком на дітях.

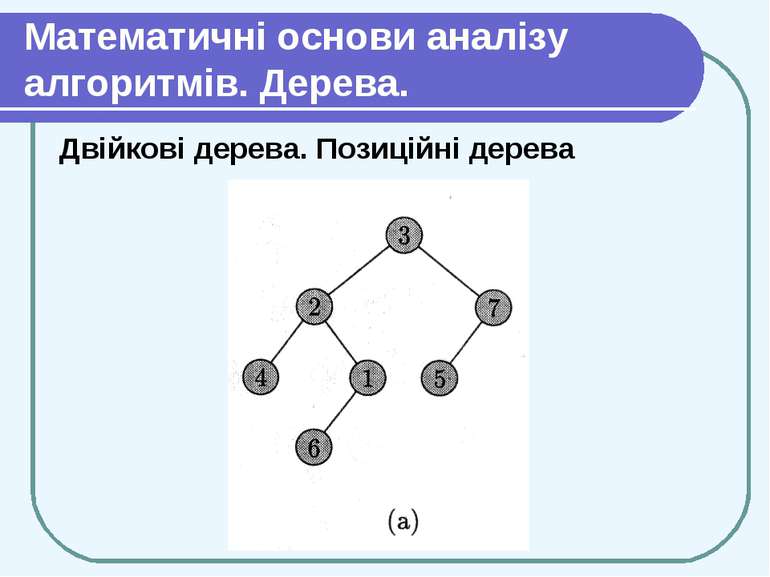
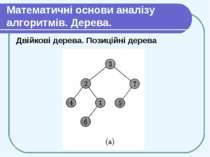
Математичні основи аналізу алгоритмів. Дерева. Двійкові дерева. Позиційні дерева Двійкове дерево (binary tree) можна визначити рекурсивно як скінченний набір вершин, який: або пустий (не містить вершин), або розбитий на три частини, які не перетинаються: вершину, що називається коренем (root), двійкове дерево, що називається лівим піддеревом (left subtree) кореня, і двійкове дерево, що називається правим піддеревом (right subtree) кореня. Двійкове дерево, що не містить вершин, називається пустим (empty). Воно позначається NIL.

Математичні основи аналізу алгоритмів. Дерева. Двійкові дерева. Позиційні дерева

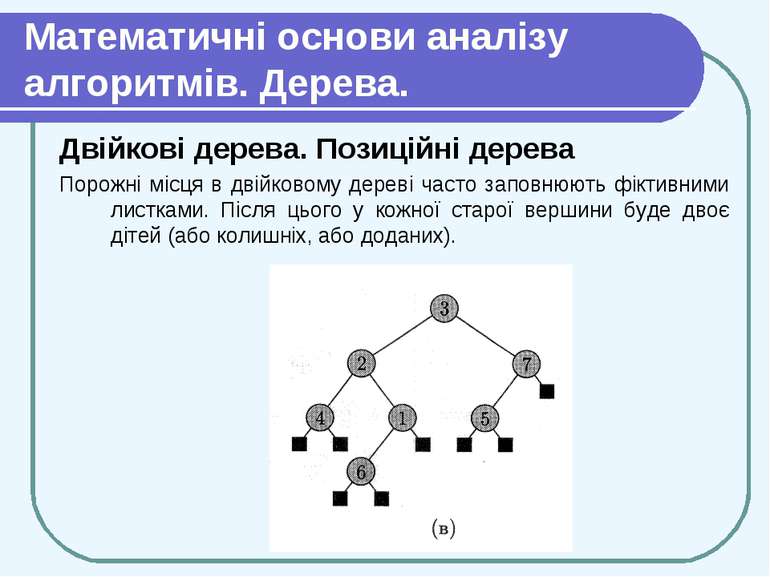
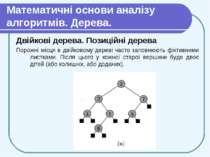
Математичні основи аналізу алгоритмів. Дерева. Двійкові дерева. Позиційні дерева Порожні місця в двійковому дереві часто заповнюють фіктивними листками. Після цього у кожної старої вершини буде двоє дітей (або колишніх, або доданих).

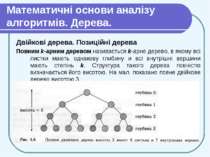
Математичні основи аналізу алгоритмів. Дерева. Двійкові дерева. Позиційні дерева Можна визначити аналоги двійкових дерев для дерев більшого степеня: двійкові дерева (бінарні) є окремим випадком k-арних дерев при k = 2. Позиційне дерево визначається як кореневе дерево, в якому діти будь-якої вершини помічені різними цілими додатними числами, які є їх номерами. При цьому у кожної вершини є вакансії для дітей номер 1, 2, 3 і так далі, з яких деякі (скінченна кількість) заповнені, а інші вільні. При цьому k-арним деревом називається позиційне дерево, що не має вершин з номерами більшими за k.

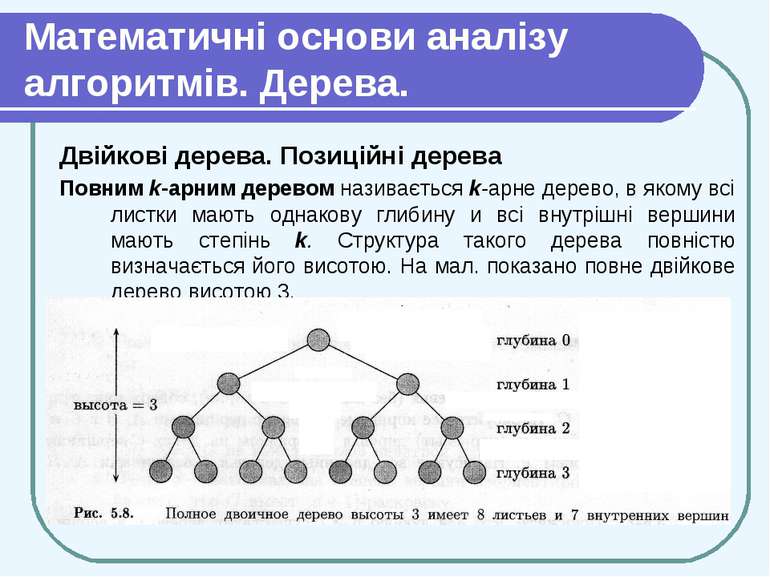
Математичні основи аналізу алгоритмів. Дерева. Двійкові дерева. Позиційні дерева Повним k-арним деревом називається k-арне дерево, в якому всі листки мають однакову глибину и всі внутрішні вершини мають степінь k. Структура такого дерева повністю визначається його висотою. На мал. показано повне двійкове дерево висотою 3.

Математичні основи аналізу алгоритмів. Дерева. Двійкові дерева. Позиційні дерева Підрахуємо, скільки листків має повне k-арне дерево висотою h. Корінь є єдиною вершиною глибини 0, його k дітей є вершинами глибини 1, їх дітьми є k2 вершин глибини 2 і так далі аж до kh листків глибини h. Висота k-арного дерева з n листками дорівнює logkn (таке дерево існує, тільки якщо цей логарифм цілий). Кількість внутрішніх вершин повного k-арного дерева висоти h дорівнює (сума чл. геом. прогрес.) Зокрема, для повного двійкового дерева кількість внутрішніх вершин на одиницю менша кількості листків.

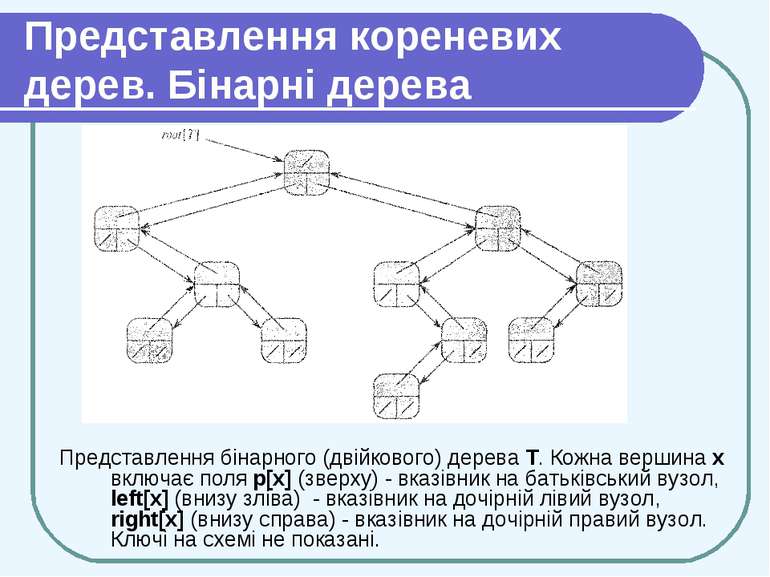
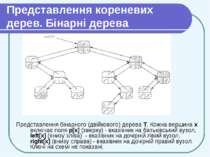
Представлення кореневих дерев. Бінарні дерева Представлення бінарного (двійкового) дерева Т. Кожна вершина х включає поля р[х] (зверху) - вказівник на батьківський вузол, left[x] (внизу зліва) - вказівник на дочірній лівий вузол, right[x] (внизу справа) - вказівник на дочірній правий вузол. Ключі на схемі не показані.

Представлення кореневих дерев. Бінарні дерева Якщо р [х] = nil, то х — корінь дерева. Якщо у вузла х немає дочірніх вузлів, то left [х] = right [х] = nil. Атрибут root [T] вказує на кореневий вузол дерева T. Якщо root [T] = NIL, то дерево Т пусте.

БАЖАЮ УСПІХІВ!!!