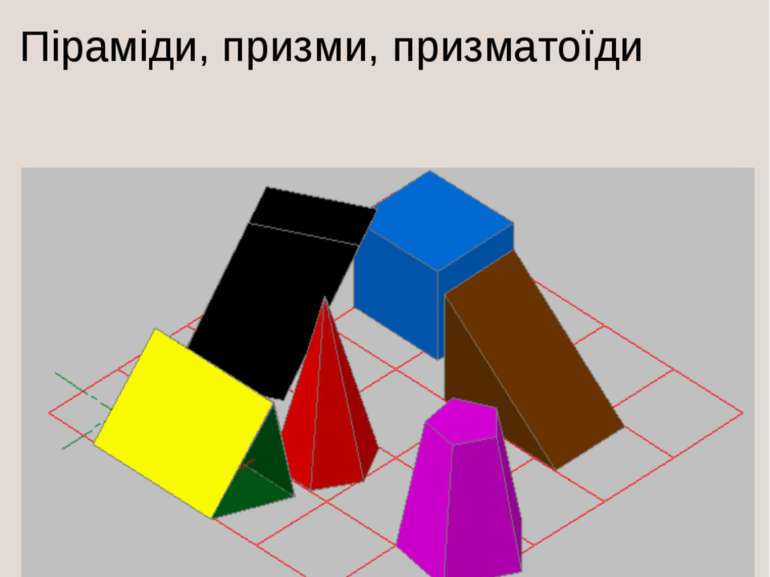
Презентація на тему:
Побудова кривих ліній. Поверхні. Класифікація поверхонь. Точки на поверхні.

Лекція 3 Криві лінії. Поверхні. Класифікація поверхонь. Точки на поверхні. Кафедра нарисної геометрії, інженерної та комп'ютерної графіки

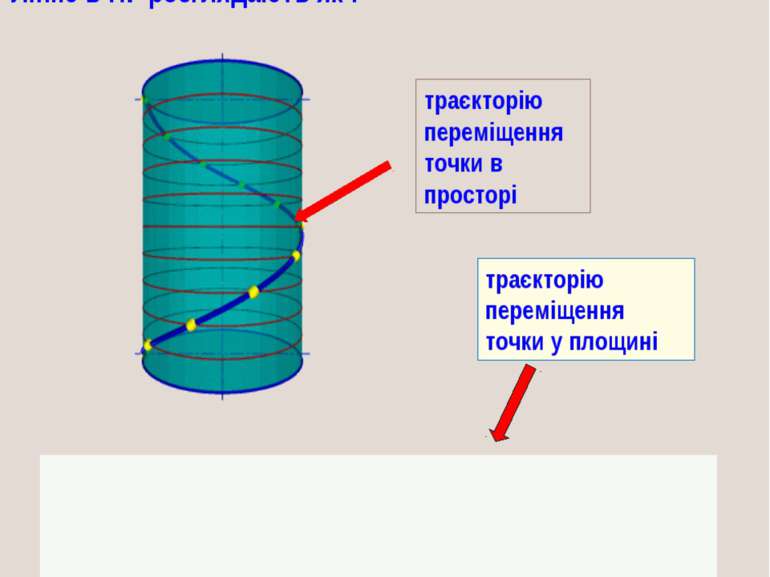
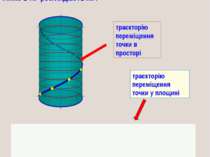
Лінію в НГ розглядають як : траєкторію переміщення точки в просторі траєкторію переміщення точки у площині 1. КРИВІ ЛІНІЇ

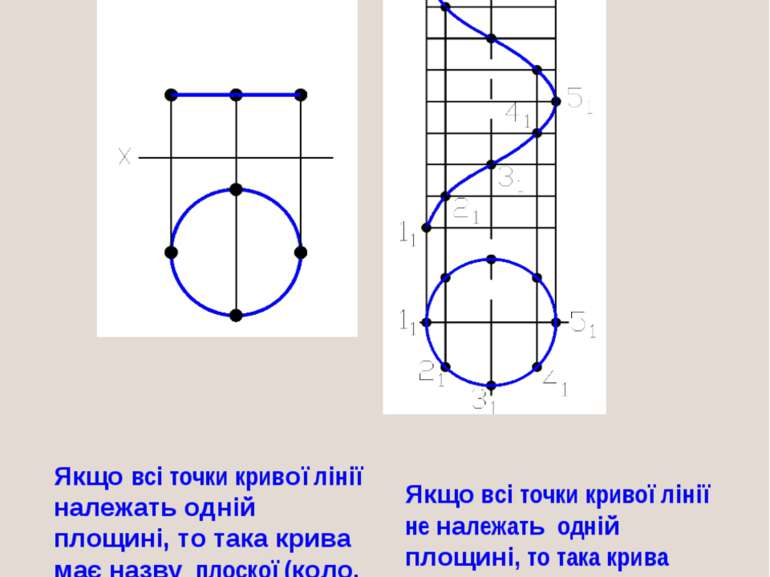
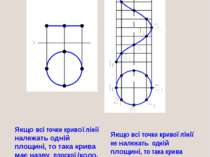
Якщо всі точки кривої лінії належать одній площині, то така крива має назву плоскої (коло, еліпс, парабола, гіпербола). Якщо всі точки кривої лінії не належать одній площині, то така крива має назву просторова (гвинтова лінія).

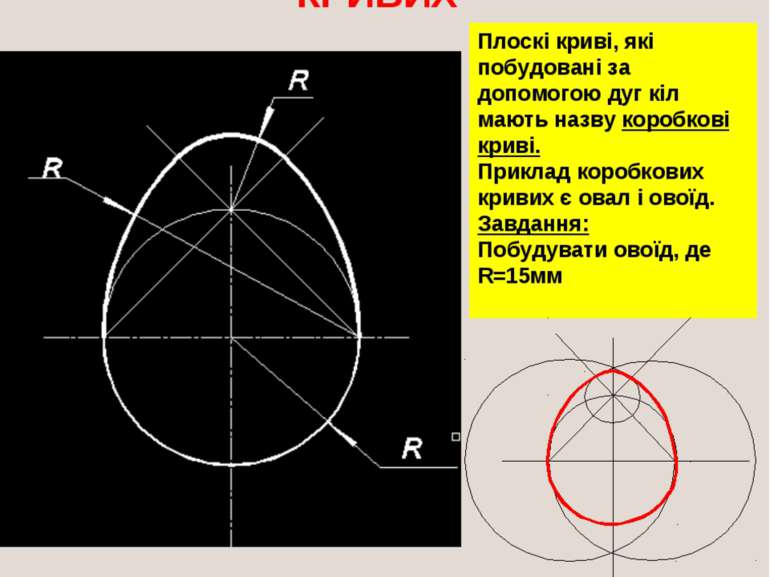
ПОБУДОВА КОРОБКОВИХ КРИВИХ Плоскі криві, які побудовані за допомогою дуг кіл мають назву коробкові криві. Приклад коробкових кривих є овал і овоїд. Завдання: Побудувати овоїд, де R=15мм

АЛГЕБРАІЧНІ КРИВІ Криві, які задаються алгебраїчним рівнянням мають назву алгебраїчні. Ступінь рівняння визначає порядок кривої лінії. Лінією 1-го порядку є пряма. Криві 2-го порядку це еліпс, парабола, гіпербола. Еліпс – є окремий випадок проекції кола. Завдання: Побудувати еліпс по двом колам. R1=20мм, R2=40мм. А В С D

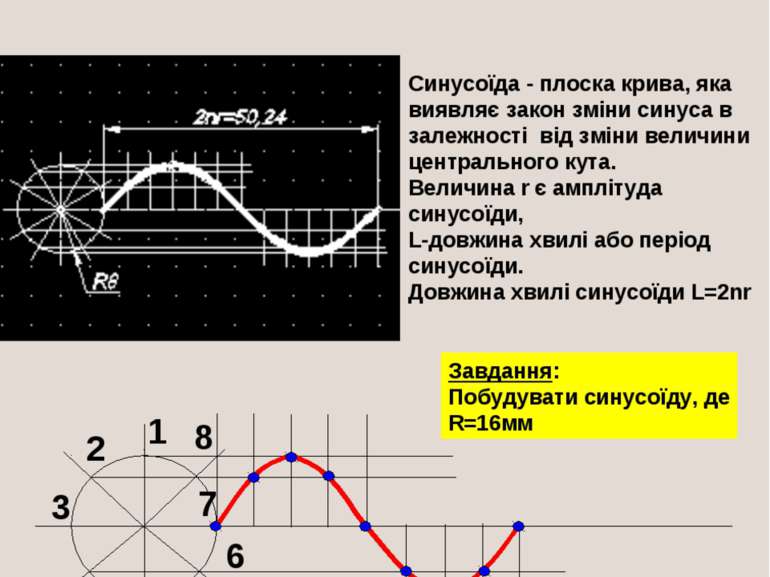
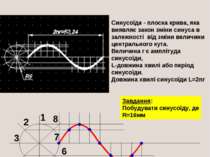
СИНУСОЇДА Синусоїда - плоска крива, яка виявляє закон зміни синуса в залежності від зміни величини центрального кута. Величина r є амплітуда синусоїди, L-довжина хвилі або період синусоїди. Довжина хвилі синусоїди L=2nr Завдання: Побудувати синусоїду, де R=16мм 1 2 3 4 5 6 7 8

СПІРАЛЬ АРХІМЕДА Плоска крива яка описується точкою що робить одночасно два рухи – одне вздовж радіусу-вектору, яке обертається навколо полюса,а друге вздовж кола.

ЕВОЛЬВЕНТА Евольвентою кола є траєкторія (шлях) точки прямої лінії коли ця пряма котиться без ковзання по нерухомому колу. Для побудові евольвенти задане коло діаметром D ділять на декілька рівних частин які нумерують. З кінцевої точки 7 проводять касательну до кола і відкладають на ній довжину кола яка дорівнюється nD . Довжину кола ділять також на рівні частини та з точок ділення проводять касательні на яких відкладають відрізки відповідно: 1 = nD/8; 2 = 2nD/8; 3 = 3nD/8 і т.д. Завдання: Побудувати евольвенту кола D=20мм

Циклоїдні криві Циклоїдними називають такі незамкнуті плоскі криві, які описують точки кола, яке котиться без ковзання вздовж нерухомого кола або вздовж прямої. Якщо коло котиться вздовж прямої, то ії точки описують циклоїду. Якщо коло котиться вздовж кола ззовні, то ії точки описують епіциклоїду. Якщо коло котиться вздовж кола всередині, то ії точки описують гіпоциклоїду.

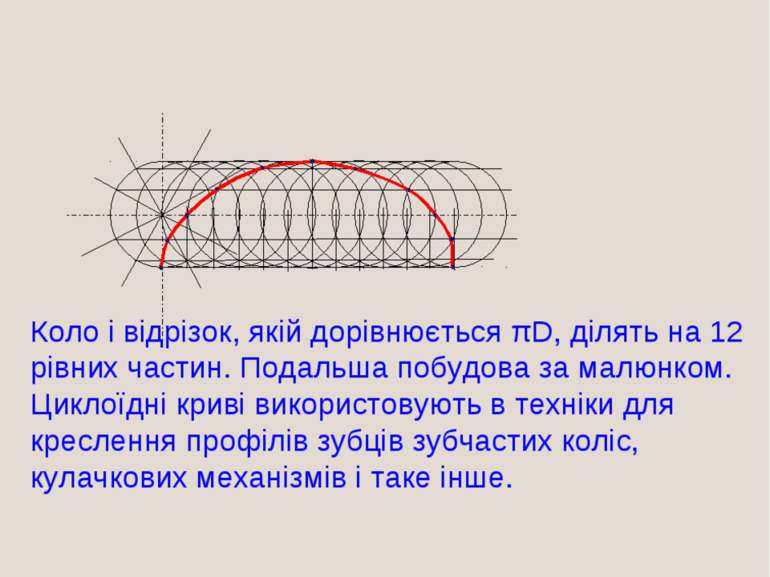
Побудова ЦИКЛОИДИ Коло і відрізок, якій дорівнюється πD, ділять на 12 рівних частин. Подальша побудова за малюнком. Циклоїдні криві використовують в техніки для креслення профілів зубців зубчастих коліс, кулачкових механізмів і таке інше.

Завдання для лабораторної роботи “ Криві плоскі лінії ”

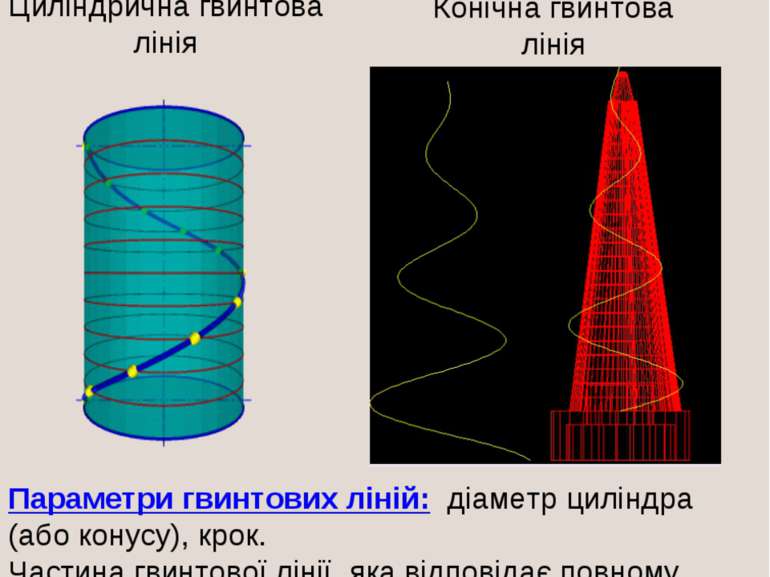
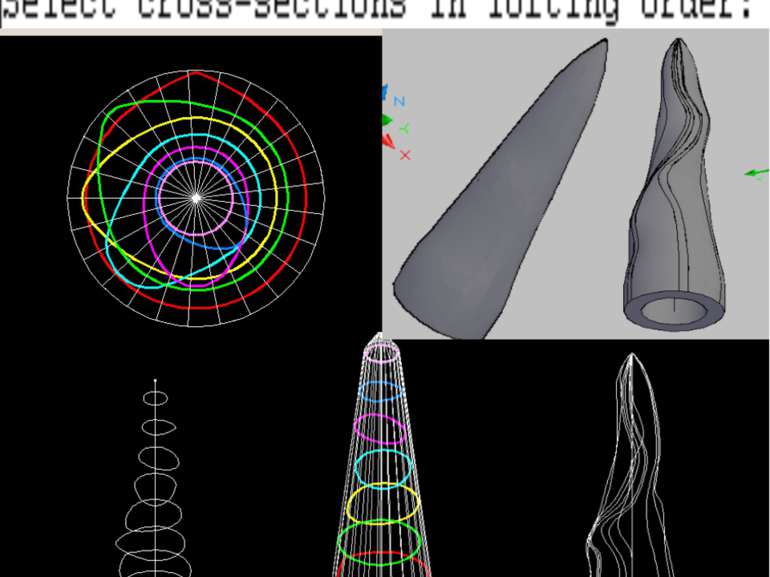
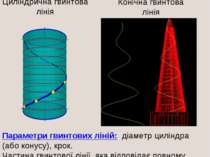
Просторові криві Циліндрична гвинтова лінія Конічна гвинтова лінія Параметри гвинтових ліній: діаметр циліндра (або конусу), крок. Частина гвинтової лінії, яка відповідає повному оберту твірної циліндра (або конусу) і переміщенню по неї точки на відстані кроку,називається витком.

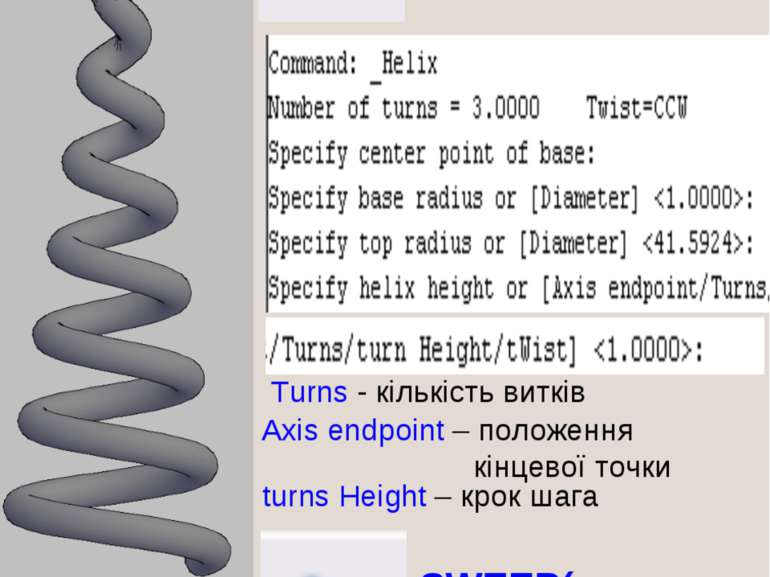
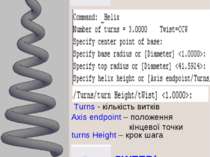
HELIX(гвинтова) Turns - кількість витків Axis endpoint – положення кінцевої точки turns Height – крок шага tWist - SWEEP(

EXTRUDE (ВИШТОВХНИ) дозволяє замкнені двовимірні об’єкти перетворити на тривимірні. Одночасно можна оперувати з декількома об’єктами, такими як полілінія, багатокутник, коло, еліпс, сплайн, кільце та область. Command: еxtrude Select objects: (Виберіть об’єкти): Після вибору об’єктів необхідно відповісти на наступні питання: Path/: (Траекторія): Height of Extrusion (Глибина виштовхування) може бути задана числом зі знаком або , який визначає напрямок виштовхування вздовж осі Z ПСК. Опція Extrusion taper angle : (Кут звуження :) надає можливість створення тіл з не паралельними бічними гранями. Кут звуження задається в межах 90 (при додатних значеннях кута фігура звужується, при від’ємних – розширюється). Опція Path (Траекторія) дозволяє задати висоту та напрямок виштовхування за допомогою допоміжного об’єкту: Select рath: (Оберіть траекторію:).

ЛОГІЧНІ КОМАНДИ Для створення більш складних об’єктів з простих використовуються команди UNION (ОБ’ЄДНАТИ) Викликаються команди з падаючого меню Modify, пункт Solids Editing, або з панелі Solids Editing. Command: union Select objects: (Виберіть об’єкти):

SUBTRACT (ВІДНЯТИ) Command: subtract Select solids and regions to subtract from... (Виберіть тіла або області, з яких буде виконане віднімання):

Command: intersect Select objects: (Виберіть об’єкти): INTERSECT (ПЕРЕТНУТИ).

КОМАНДИ ПОБУДОВИ ГРАФІЧНИХ ПРИМІТИВІВ Команди створення графічних примітивів, команди обертання та видавлювання викликаються з падаючого меню Draw, пункт Solids, або з панелі Solids. 3.1. Команда BOX (ПАРАЛЕЛЕПІПЕД) дозволяє створити прямокутний паралелепіпед або куб. Для цього необхідно задати: дві кінцеві точки його діагоналі (рис.4а); або дві кінцеві точки діагоналі його основи та висоту ; або центр та одну з його вершин; або центр паралелепіпеда та його розміри. Незалежно від способу завдання ребра паралелепіпеда розташовуються паралельно осям X,Y та Z поточної системи координат (ПСК). Command: box Center/ (Центр/ ): Опція Corner of box (Вершина паралелепіпеда) задає одну з його вершин; Опція Оther corner (Друга вершина) задає діагонально протилежну другу його вершину. Якщо координати z обох точок однакові (тобто задана не діагональ паралелепіпеда, а діагональ його основи), необхідно задати висоту паралелепіпеда: Height (Висота): Опція Center( Центр) задає центральну точку паралелепіпеда, після чого задається одна з його вершин або розміри паралелепіпеда: Length (Довжина); Width (Ширина); Height (Висота). Опція Cube (Куб) дозволяє створити куб. 3.2. 3.3. Команда SPHERE (СФЕРА) дозволяє створити сферу заданого радіуса з центром в заданій точці. Command: sphere Center of sphere (Центр сфери ): Diameter/ of sphere (Діаметр/ сфери) : 3.4. Команда CONE (КОНУС) дозволяє створити прямий круговий або еліптичний конус, основа якого (коло або еліпс) перпендикулярна до осі конуса. Command: cone Elliptical/ (Еліптичний/ ) : Опція Elliptical (Еліптичний) застосовуться для створення еліптичного конуса. Опція ( ): дозволяє створити прямий круговий конус. Для його створення після задання центру основи необхідно ввести радіус (або діаметр) кола основи та висоту конуса. Height (Висота) конуса задається числом зі знаком або , який визначає орієнтацію конуса вздовж осі Z ПСК. 3.5. Команда CYLINDER (ЦИЛІНДР) дозволяє створити циліндр аналогічно тому, як створюється конус командою CONE (КОНУС) і відрізняється від неї тим, що замість вершини конуса задається друга кінцева точка осі циліндра: Center of other end (Центр другого кінця). 3.6. КОМАНДА ОБЕРТАННЯ REVOLVE (ОБЕРТАЙ) дозволяє створювати тіла обертання. Обертати навколо заданої осі можливо лише один об’єкт (замкнений), яким може бути полілінія, багатокутник, коло, еліпс, сплайн, кільце та область. Об’єкт не може бути тривимірним, може дотикатися осі , але не повинен перетинатися з нею. Додатний напрямок обертання визначається за правилом правої руки. 6. ЛОГІЧНІ КОМАНДИ Для створення більш складних об’єктів з простих використовуються команди UNION (ОБ’ЄДНАТИ), SUBTRACT (ВІДНЯТИ) та INTERSECT (ПЕРЕТНУТИ). Викликаються команди з падаючого меню Modify, пункт Solids Editing, або з панелі Solids Editing. Command: union Select objects: (Виберіть об’єкти): Command: subtract Select solids and regions to subtract from... (Виберіть тіла або області, з яких буде виконане віднімання): Select objects: (Виберіть об’єкти): Select solids and regions to subtract.... (Виберіть тіла або області, які віднімаються): Select objects: (Виберіть об’єкти): Команда WEDGE (КЛИН) дозволяє створити клин, основа якого паралельна площині ХУ ПСК, а нахилена грань розташована вздовж осі Х (рис. 4б). Опціяі цієї команди аналогічні опціяам команди ВОХ а б Рис.4 Для однієї фігури задана висота, для другої траекторія виштовхування, для третьої фігури крім висоти заданий кут звуження (рис. 7б, рис.7в та рис.7г відповідно). а б в г Рис.7 Command: intersect Select objects: (Виберіть об’єкти): На рис.8 зображені фігури, які отримані з паралелепіпеда та циліндра (після суміщення вертикальних осей) за допомогою цих команд (рис.8а - union, рис.8б - subtract, рис.8в - intersect). а б в Рис.8

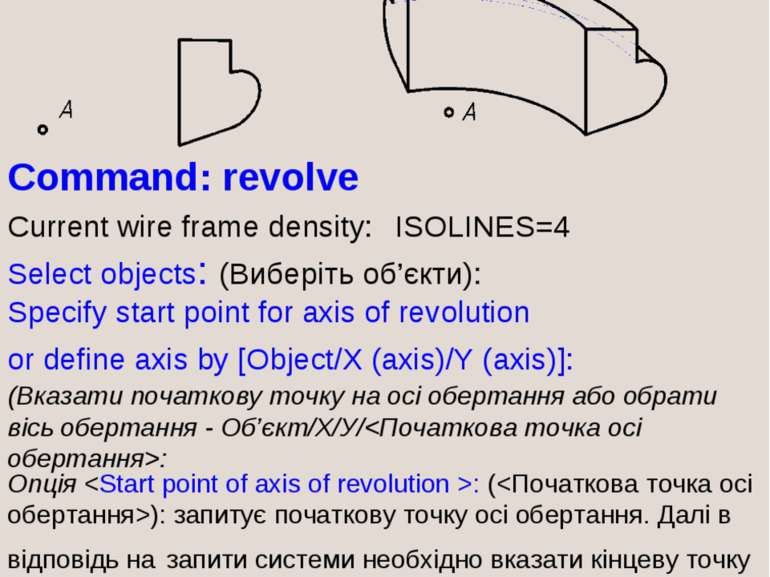
Command: revolve Current wire frame density: ISOLINES=4 Select objects: (Виберіть об’єкти): Specify start point for axis of revolution or define axis by [Object/X (axis)/Y (axis)]: (Вказати початкову точку на осі обертання або обрати вісь обертання - Об’єкт/Х/У/: Опція : (): запитує початкову точку осі обертання. Далі в відповідь на запити системи необхідно вказати кінцеву точку осі обертання та кут обертання. Опція Object (Об’єкт) дозволяє обрати відрізок або прямолінійний сегмент полілінії як вісь обертання.

КОМАНДИ ПОБУДОВИ ГРАФІЧНИХ ПРИМІТИВІВ Команди створення графічних примітивів, команди обертання та видавлювання викликаються з падаючого меню Draw, пункт Solids, або з панелі Solids. Команда BOX (ПАРАЛЕЛЕПІПЕД) дозволяє створити прямокутний паралелепіпед або куб. Для цього необхідно задати: дві кінцеві точки його діагоналі або дві кінцеві точки діагоналі його основи та висоту ; або центр та одну з його вершин; або центр паралелепіпеда та його розміри. Незалежно від способу завдання ребра паралелепіпеда розташовуються паралельно осям X,Y та Z поточної системи координат (ПСК).

Command: box Center/ (Центр/ ): Опція Corner of box (Вершина паралелепіпеда) задає одну з його вершин; Опція Оther corner (Друга вершина) задає діагонально протилежну другу його вершину. Якщо координати z обох точок однакові (тобто задана не діагональ паралелепіпеда, а діагональ його основи), необхідно задати висоту паралелепіпеда: Height (Висота): Опція Center( Центр) задає центральну точку паралелепіпеда, після чого задається одна з його вершин або розміри паралелепіпеда: Length (Довжина); Width (Ширина); Height (Висота). Опція Cube (Куб) дозволяє створити куб.

Команда WEDGE (КЛИН) дозволяє створити клин, основа якого паралельна площині ХУ ПСК, а нахилена грань розташована вздовж осі Х (рис. 4б). Опціяі цієї команди аналогічні опціяам команди ВОХ Команда SPHERE (СФЕРА) дозволяє створити сферу заданого радіуса з центром в заданій точці. Command: sphere Center of sphere (Центр сфери ): Diameter/ of sphere (Діаметр/ сфери) :

Команда CONE (КОНУС) дозволяє створити прямий круговий або еліптичний конус, основа якого (коло або еліпс) перпендикулярна до осі конуса. Command: cone Elliptical/ (Еліптичний/ ) : Опція Elliptical (Еліптичний) застосовуться для створення еліптичного конуса. Опція ( ): дозволяє створити прямий круговий конус. Для його створення після задання центру основи необхідно ввести радіус (або діаметр) кола основи та висоту конуса. Height (Висота) конуса задається числом зі знаком або , який визначає орієнтацію конуса вздовж осі Z ПСК.

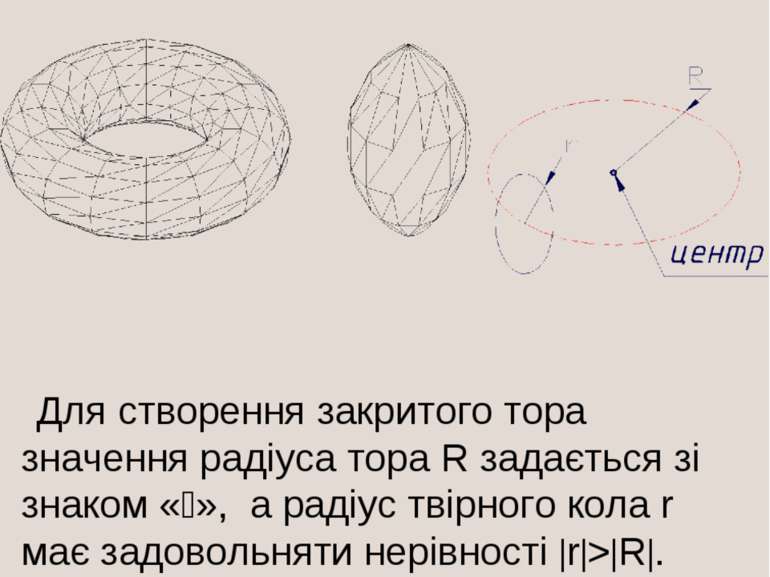
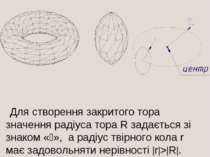
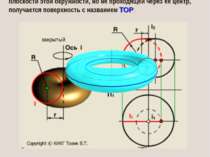
. Команда CYLINDER (ЦИЛІНДР) дозволяє створити циліндр аналогічно тому, як створюється конус командою CONE (КОНУС) і відрізняється від неї тим, що замість вершини конуса задається друга кінцева точка осі циліндра: Center of other end (Центр другого кінця). Команда TORUS (ТОР) дозволяє створити тор (рис.5) Command: torus Current wire frame density: ISOLINES=4 Specify center of torus : (Вказати центр тора :) Specify radius of torus or [Diameter]: (Вказати радіус тора або (Діаметр):) Specify radius of tube or [Diameter]: ( Вказати радіус твірного кола або (Діаметр):)

Для створення закритого тора значення радіуса тора R задається зі знаком « », а радіус твірного кола r має задовольняти нерівності r > R .

Геометричне тіло - замкнута частина простору, яка обмежена плоскими або кривими поверхнями. В елементарній геометрії поверхня є границя тіла або слід лінії яка рухається. Товщини поверхня не має.

ЗОБРАЖЕННЯ БОГАТОГРАННИКІВ

ВИДИ МНОГОРАННИКІВ Піраміди, призми, призматоїди

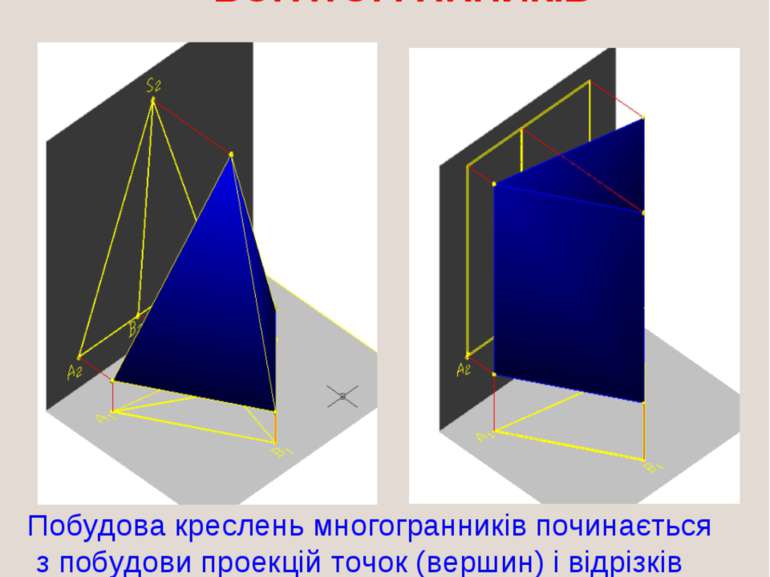
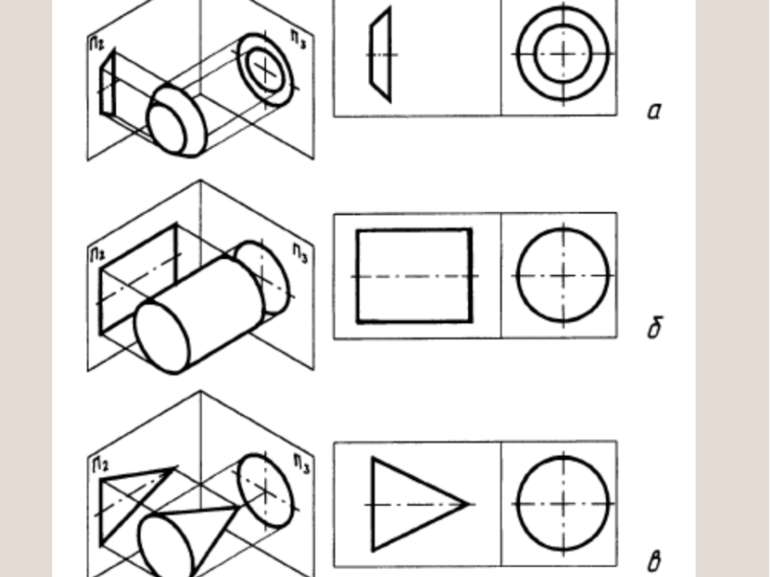
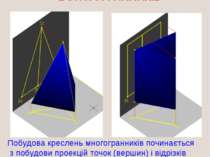
КРЕСЛЕННЯ БОГАТОГРАННИКІВ Побудова креслень многогранників починається з побудови проекцій точок (вершин) і відрізків прямих (ребер).

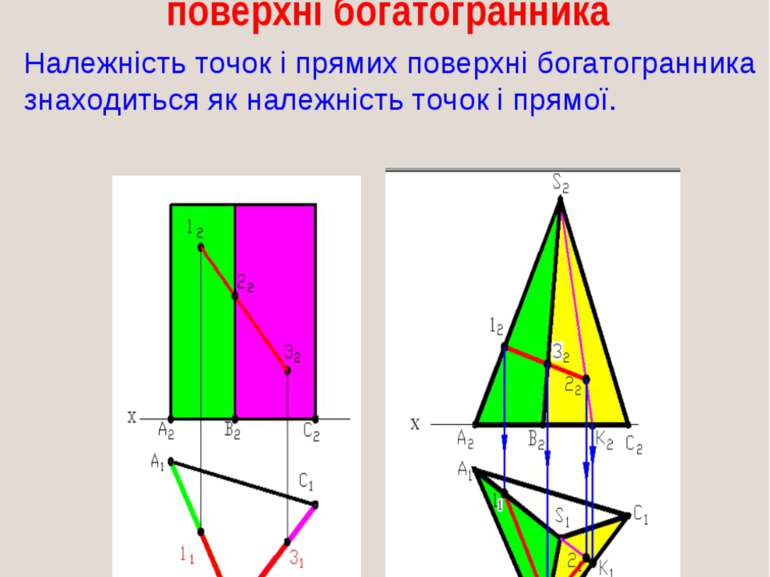
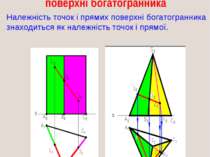
Належність точки і прямої поверхні богатогранника Належність точок і прямих поверхні богатогранника знаходиться як належність точок і прямої.

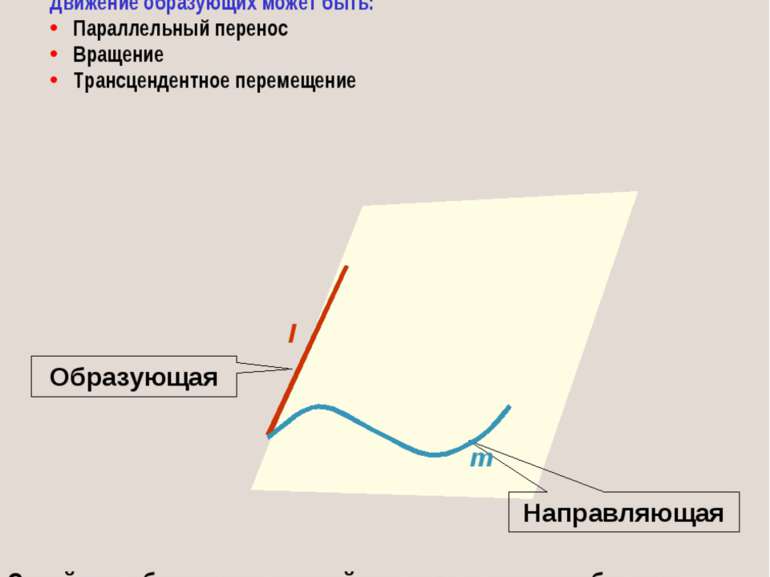
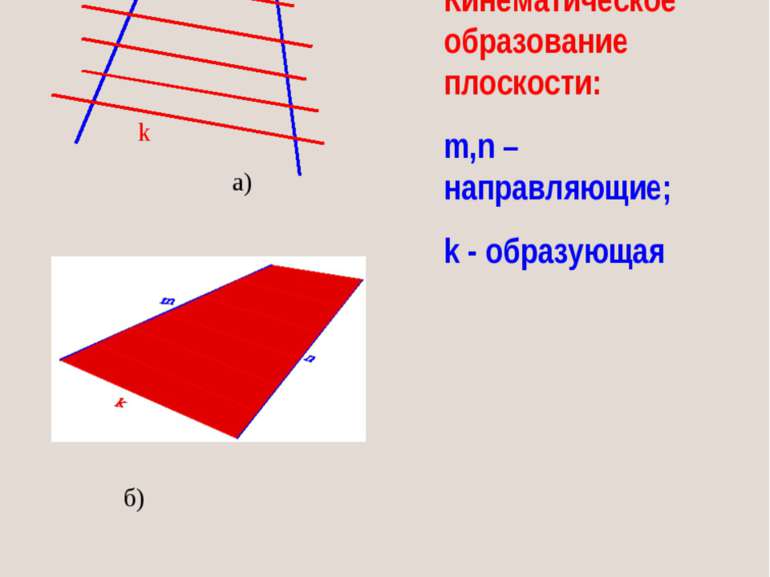
В НГ поверхность рассматривают как множество последовательных положений движущейся линии в пространстве. Линию, перемещающуюся в пространстве называют ОБРАЗУЮЩЕЙ. Образующие могут быть прямыми или кривыми, сохранять или изменять свою форму в процессе перемещения. Закон перемещения образующей также может быть различным: она может перемещаться вдоль некоторых линий прямых или кривых, называемых НАПРАВЛЯЮЩИМИ. Такой принцип образования поверхности называют КИНЕМАТИЧЕСКИМ. 2. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТИ

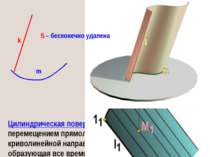
КИНЕМАТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ ПОВЕРХНОСТИ l Образующая Направляющая m Семейство образующих и семейство направляющих образуют непрерывный каркас поверхности. Движение образующих может быть: Параллельный перенос Вращение Трансцендентное перемещение

а) б) Кинематическое образование плоскости: m,n – направляющие; k - образующая m n k

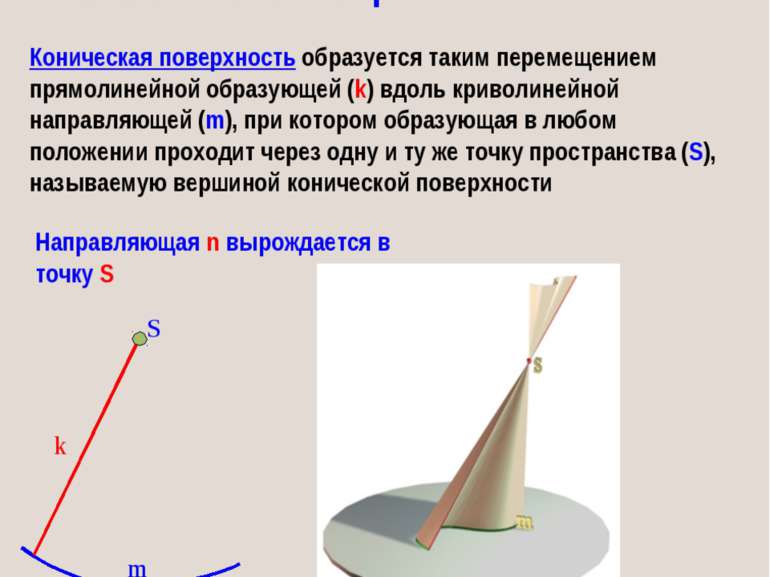
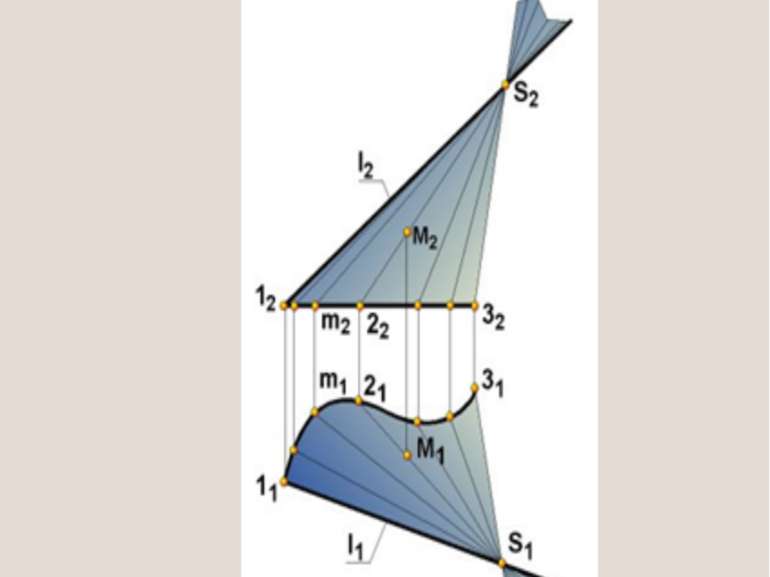
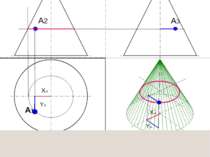
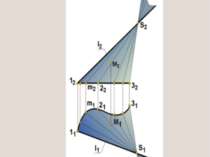
Кинематическое образование конической поверхности: S m k Коническая поверхность образуется таким перемещением прямолинейной образующей (k) вдоль криволинейной направляющей (m), при котором образующая в любом положении проходит через одну и ту же точку пространства (S), называемую вершиной конической поверхности Направляющая n вырождается в точку S

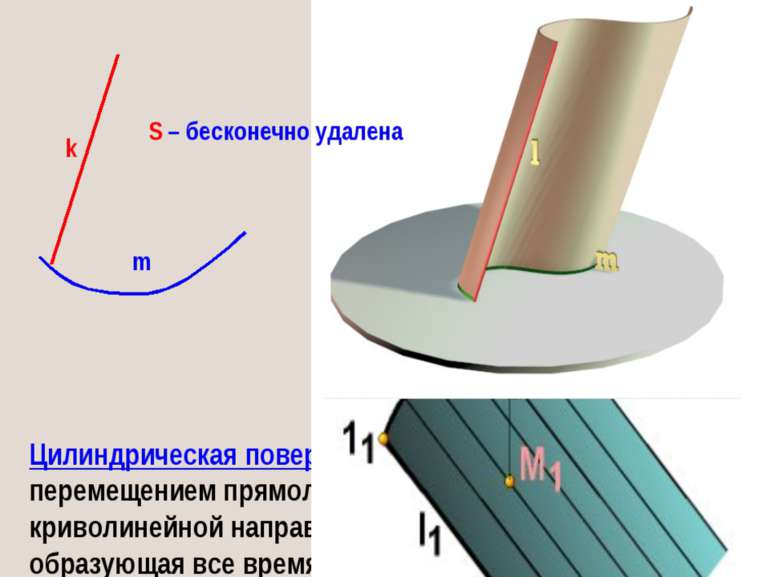
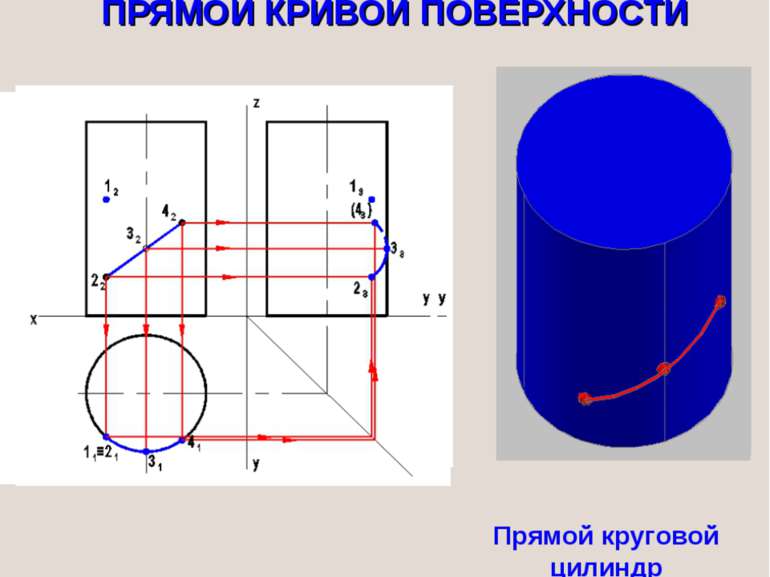
Цилиндрическая поверхность образуется таким перемещением прямолинейной образующей (k) вдоль криволинейной направляющей (m), при котором образующая все время остается параллельной заданной прямой m k Кинематическое образование цилиндрической поверхности: S – бесконечно удалена

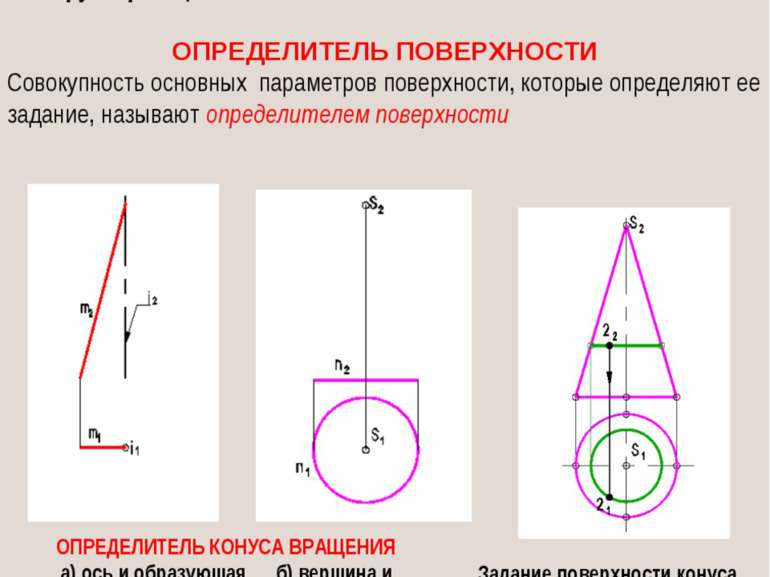
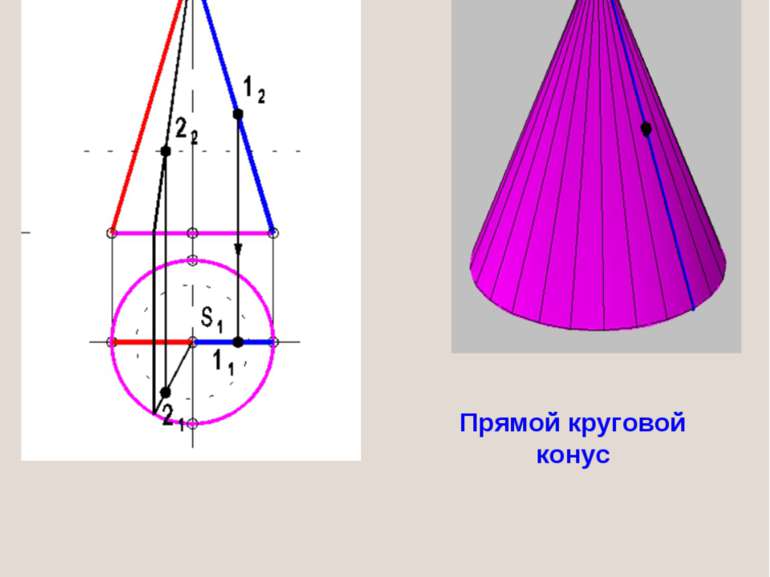
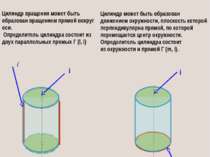
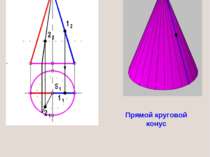
ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ Совокупность основных параметров поверхности, которые определяют ее задание, называют определителем поверхности ОПРЕДЕЛИТЕЛЬ КОНУСА ВРАЩЕНИЯ а) ось и образующая б) вершина и направляющая Задание поверхности конуса вращения очерком Поверхность считается заданной, если по одной проекции точки, принадлежащей данной поверхности, можно построить ее вторую проекцию.

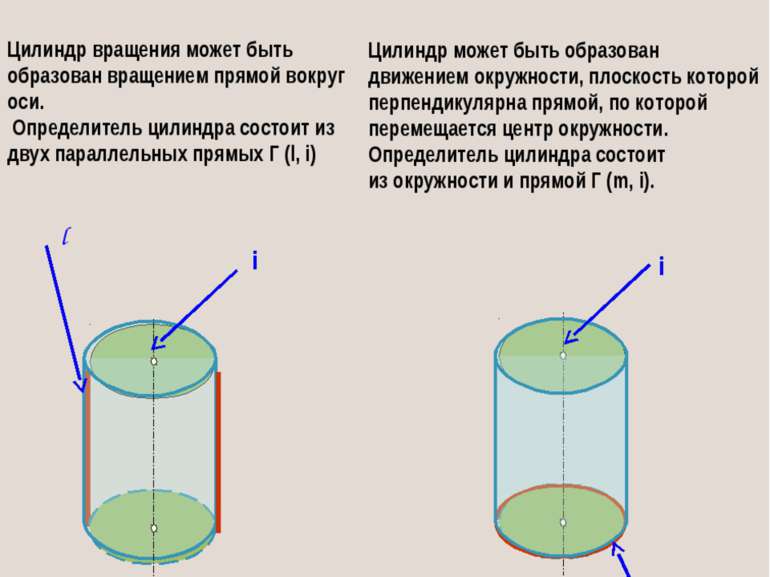
Одна и та же поверхность может быть образована несколькими способами, поэтому она может иметь различные определители. Цилиндр вращения может быть образован вращением прямой вокруг оси.  Определитель цилиндра состоит из двух параллельных прямых Г (l, i) Цилиндр может быть образован движением окружности, плоскость которой перпендикулярна прямой, по которой перемещается центр окружности. Определитель цилиндра состоит из окружности и прямой Г (m, i). i l m i

По СПОСОБУ ОБРАЗОВАНИЯ поверхности разделяются на следующие классы: Линейчатые поверхности общего вида, в том числе винтовые поверхности Поверхности вращения линейчатые и нелинейчатые. К ним принадлежат поверхности второго порядка. Поверхности второго порядка общего вида (т.е. полученные не в результате вращения) Циклические поверхности, которые могут быть образованы в результате движения окружности (постоянного или переменного диаметра) Незакономерные поверхности, называемые также топографическими или графически задаваемыми. Задаются при помощи сечений. 4. ПРИЗНАКИ КЛАССИФИКАЦИИ КРИВЫХ ПОВЕРХНОСТЕЙ

5. ЛИНЕЙЧАТЫЕ РАЗВЕРТЫВАЕМЫЕ ПОВЕРХНОСТИ Поверхность, образуемая перемещением в пространстве прямолинейной образующей, называется линейчатой. Развертываемые поверхности – это поверхности, которые всеми своими точками без разрывов и складок, могут быть совмещены с плоскостью. Это цилиндрические, конические и поверхности с ребром возврата (торсы).

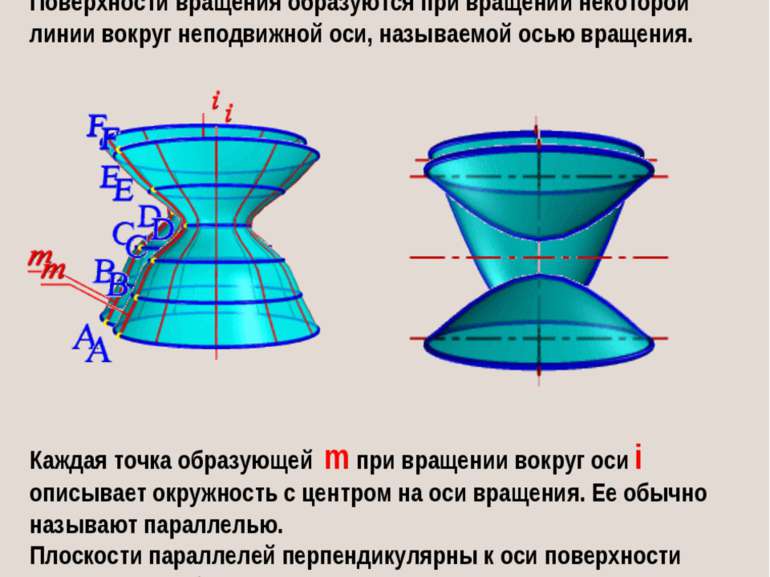
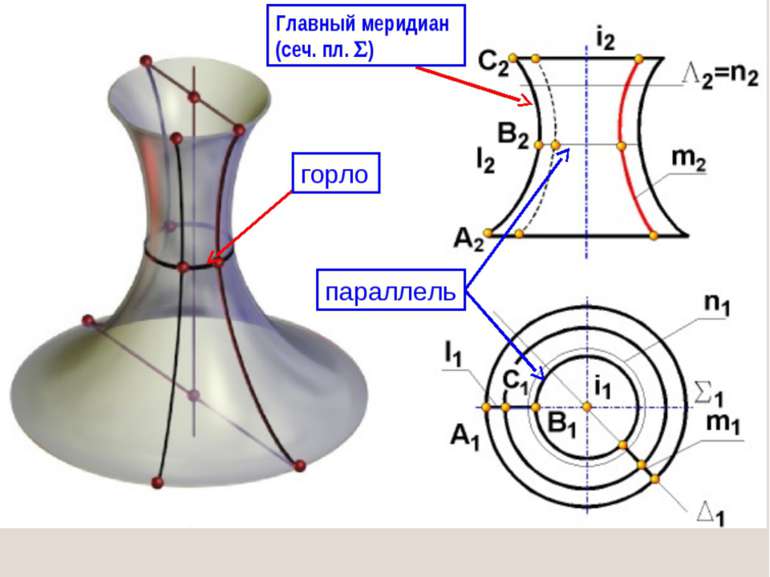
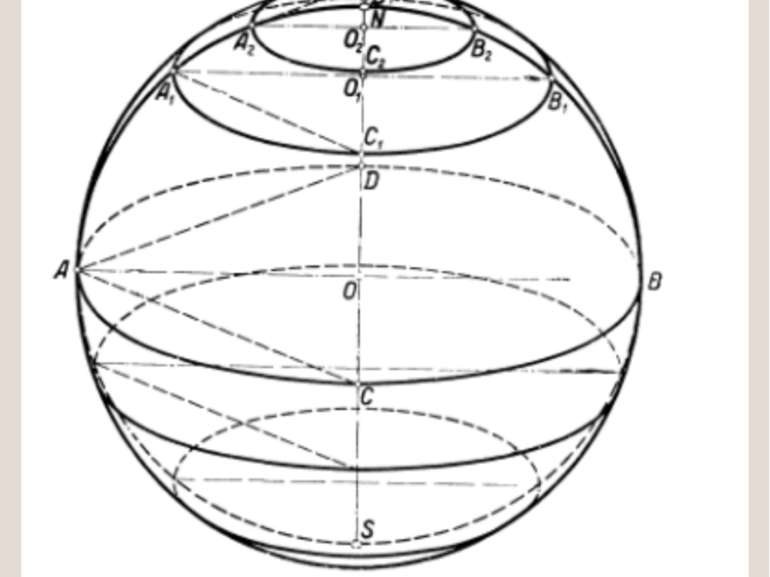
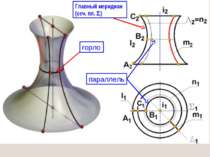
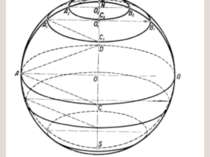
7. ПОВЕРХНОСТИ ВРАЩЕНИЯ Поверхности вращения образуются при вращении некоторой линии вокруг неподвижной оси, называемой осью вращения. Каждая точка образующей m при вращении вокруг оси i описывает окружность с центром на оси вращения. Ее обычно называют параллелью. Плоскости параллелей перпендикулярны к оси поверхности вращения. Наибольшую параллель называют экватором, наименьшую – горлом.

параллель горло Главный меридиан (сеч. пл. )

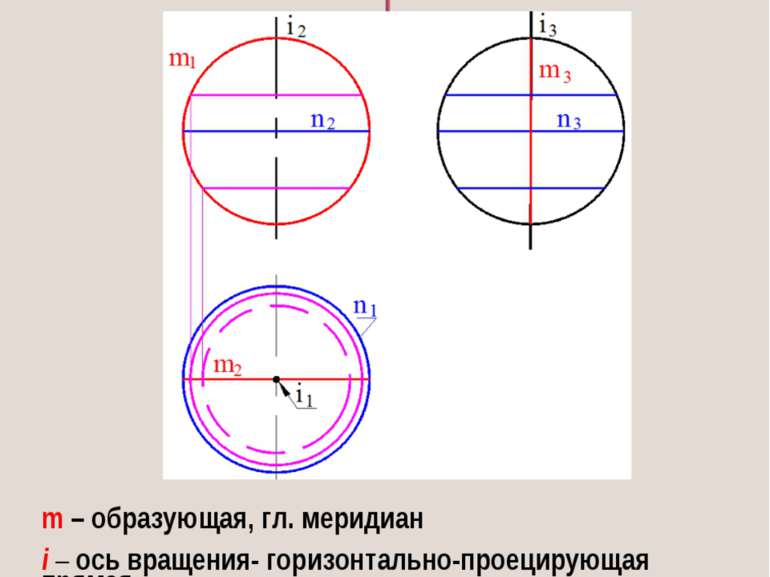
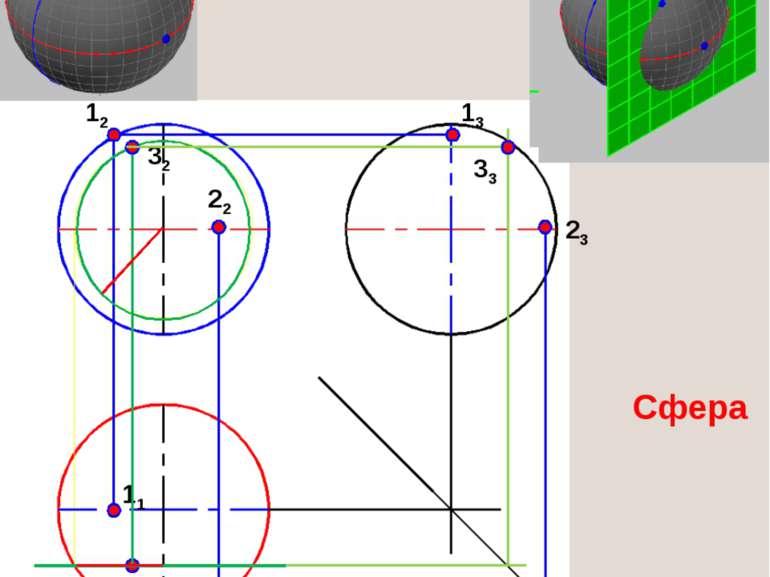
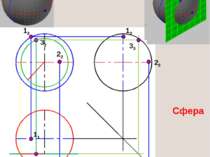
СФЕРА поверхность, получаемая путем вращения окружности вокруг собственной оси m – образующая, гл. меридиан i – ось вращения- горизонтально-проецирующая прямая n - экватор

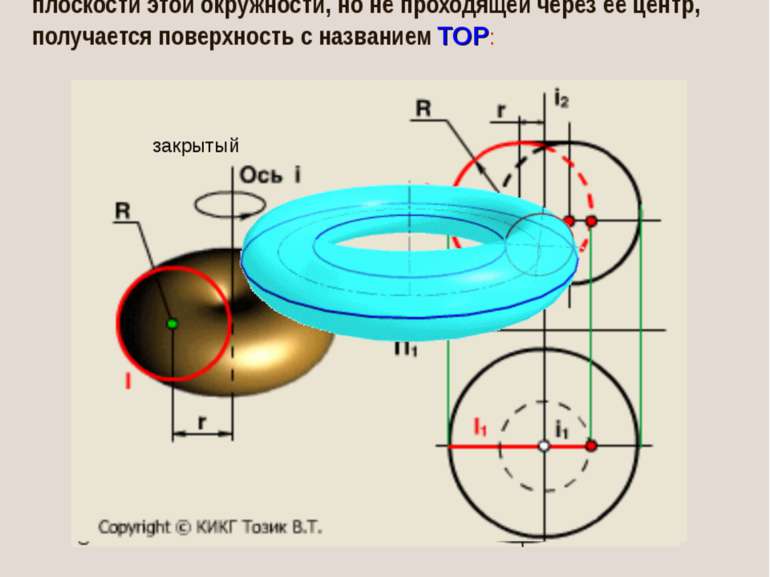
При вращении окружности (или ее дуги) вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, получается поверхность с названием ТОР:

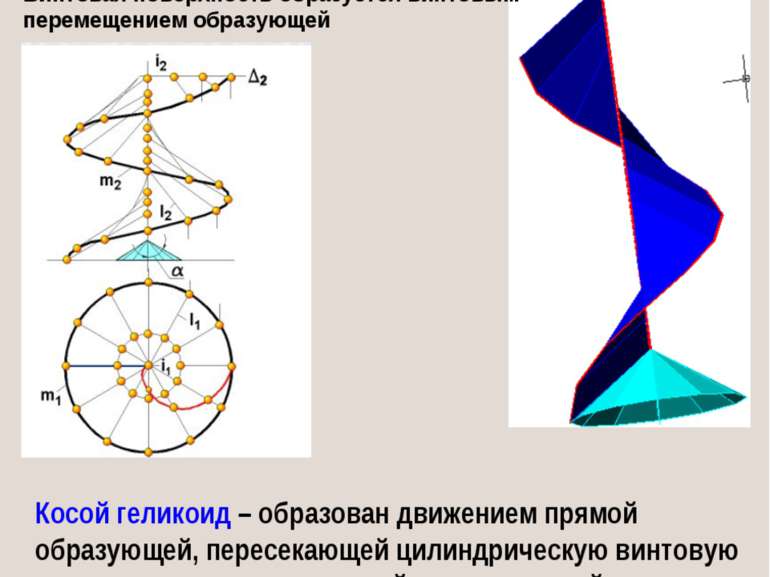
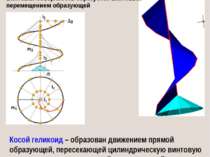
8. ВИНТОВЫЕ ПОВЕРХНОСТИ Косой геликоид – образован движением прямой образующей, пересекающей цилиндрическую винтовую линию и ее ось; роль третьей направляющей играет соосный с винтовой линией конус вращения. Винтовая поверхность образуется винтовым перемещением образующей

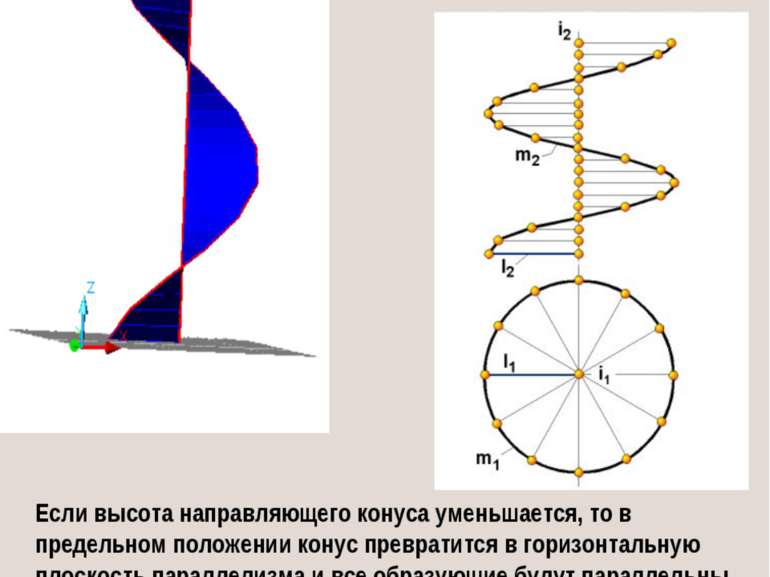
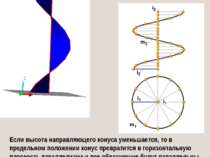
Если высота направляющего конуса уменьшается, то в предельном положении конус превратится в горизонтальную плоскость параллелизма и все образующие будут параллельны этой плоскости. В этом случае получим прямой геликоид (винтовой коноид). ПРЯМОЙ ГЕЛИКОИД

10. ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ КРИВОЙ ПОВЕРХНОСТИ Прямой круговой цилиндр

Прямой круговой конус

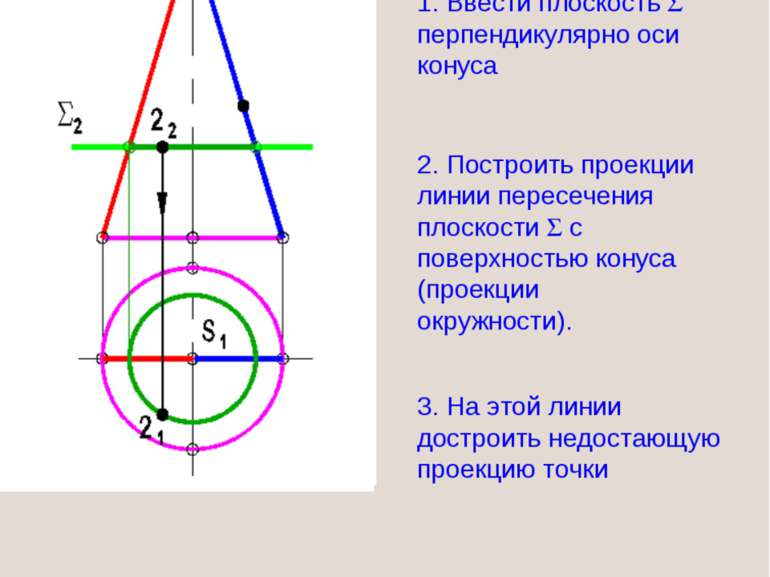
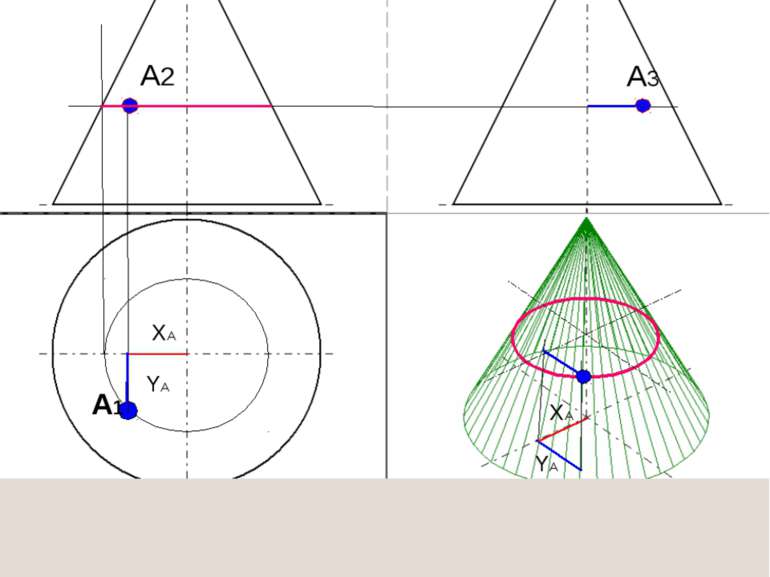
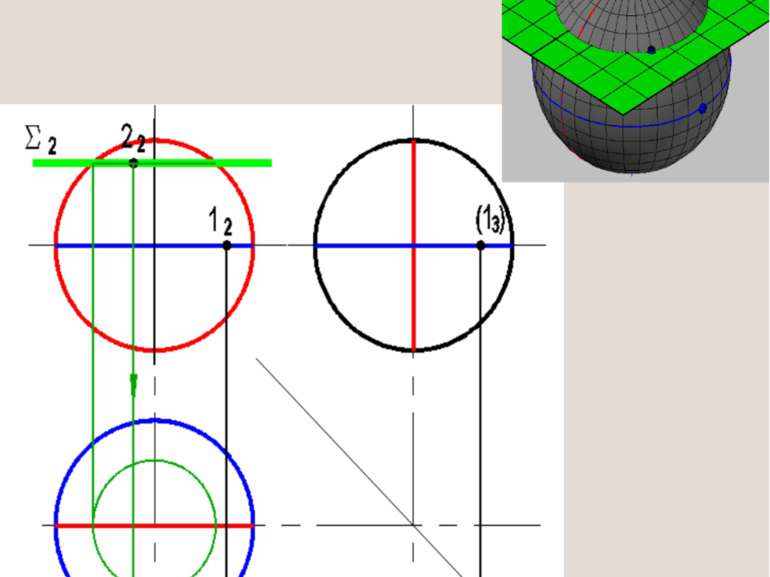
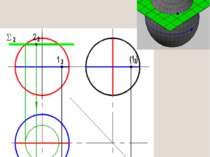
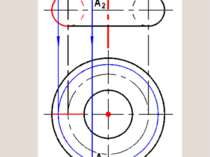
1. Ввести плоскость перпендикулярно оси конуса 2. Построить проекции линии пересечения плоскости с поверхностью конуса (проекции окружности). 3. На этой линии достроить недостающую проекцию точки Метод плоских посредников

YA A1 A2 A3 XA YA XA YA

Сфера 12 11 13 22 21 23 31 32 33

ТОЧКА НА ПОВЕРХНОСТИ ТОРА