Презентація на тему:
Задачі

Тема 4 Квадратні нерівності та системи рівнянь другого степеня Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб. Розв’язування нерівностей другого степеня з однією змінною. Аналітичний спосіб Метод інтервалів Степінь рівняння з двома змінними. Розв’язування систем рівнянь з двома змінними Розв’язування вправ. Самостійна робота Розв’язування текстових задач складанням систем рівнянь з двома змінними

Розв’язування текстових задач складанням системи рівнянь з двома змінними Умовазадачі Математична модель задачі 1. Сума двох чисел дорівнює 50, а їх добуток - 600. Знайдіть ці числа. 2. Периметр прямокутникадорівнює 100 м, а його площа – 600 м2. Знайдіть розміри прямокутника. 3. Дротом завдовжки 400 м треба 4рази обгорнути прямокутну ділянку площею 0,06 га. Які розміри повинна мати ділянка?

Приклад 1

Приклад 2

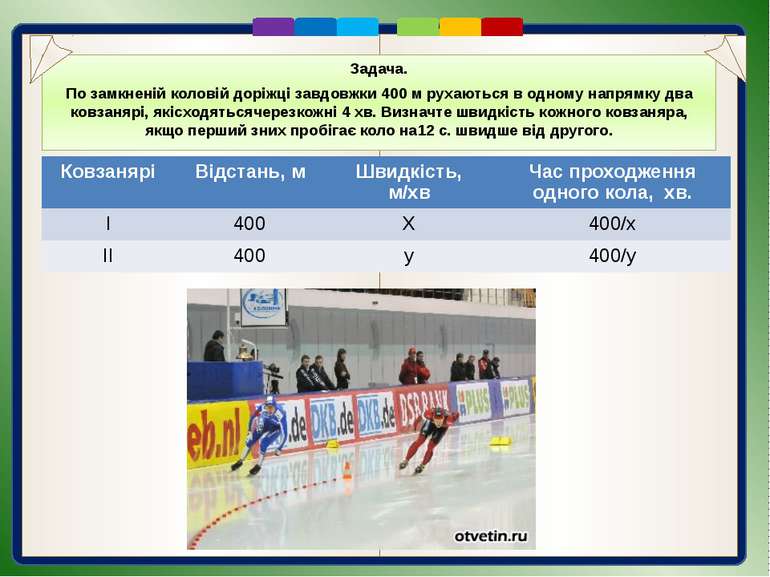
Задача. По замкненій коловій доріжці завдовжки 400 м рухаються в одному напрямку два ковзанярі, які сходяться через кожні 4 хв. Визначте швидкість кожного ковзаняра, якщо перший з них пробігає коло на 12 с. швидше від другого.

Задача. По замкненій коловій доріжці завдовжки 400 м рухаються в одному напрямку два ковзанярі, якісходятьсячерезкожні 4 хв. Визначте швидкість кожного ковзаняра, якщо перший зних пробігає коло на12 с. швидше від другого. Ковзанярі Відстань, м Швидкість, м/хв Час проходження одного кола, хв. І 400 Х 400/х ІІ 400 у 400/у

З умови задачі маємо: За 4 хв перший ковзаняр пробігає 4х метрів, а другий – 4у метрів. Перший ковзаняр за цей час пробігає на 400 м (одне коло) більше від другого. Отже, маємо ще одне рівняння: , або . Оскільки невідомі в обох рівняннях позначають одні й ті самі величини, складаємо систему рівнянь: Підставимо у перше рівняння системи замість х-у число 100, отримуємо: 2000 100=ху, або ху=200000. Отже, маємо систему Розв'язавши її способом підстановки, отримаємо два розв'язки: (500; 400) і (-400; -500). Умову задачі задовольняє тільки додатний розв'язок системи. Відповідь. Швидкість першого ковзаняра становить 500 м/хв., а другого – 400 м/хв.

Задача № 311 Спортивний майданчик прямокутної форми має площу 840 кв. м. Якщо довжину майданчика зменшити на 5 м, а ширину – збільшити на 4 м, то отримаємо прямокутник, що має таку саму площу. Знайдіть розміри майданчика. Довжина майданчика, м Ширина майданчика, м Площа майданчика х у 840 х-5 у+4 840

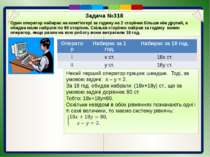
Задача №318 Один оператор набирає на комп'ютері за годину на 2 сторінки більше ніж другий, а обидва мали набрати по 80 сторінок. Скільки сторінок набрав за годину кожен оператор, якщо разом на всю роботу вони витратили 18 год. Нехай перший оператор працює швидше. Тоді, за умовою задачі: х – у = 2. За 18 год. обидва набрали: (18х+18у) ст., що за умовою задачі дорівнює 80 ст. Тобто: 18х+18у=80. Оскільки невідомі в обох рівняннях позначають одні і ті самі величини, то маємо систему рівнянь: Оператор Набирає за 1 год. Набирає за 18 год. І х ст. 18хст. ІІ у ст. 18у ст.

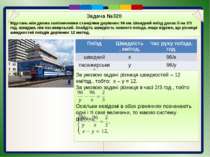
Задача №320 Відстань між двома залізничними станціями дорівнює 96 км. Швидкий поїзд долає її на 2/3 год. швидше, ніж пасажирський. Знайдіть швидкість кожного поїзда, якщо відомо, що різниця швидкостей поїздів дорівнює 12 км/год. За умовою задачі різниця швидкостей – 12 км/год., тобто: х – у = 12. За умовою задачі різниця в часі 2/3 год., тобто Оскільки невідомі в обох рівняннях позначають одні і ті самі величини, то маємо систему рівнянь: Поїзд Швидкість, км/год. Час руху поїзда, год. швидкий х 96/х пасажирський у 96/у

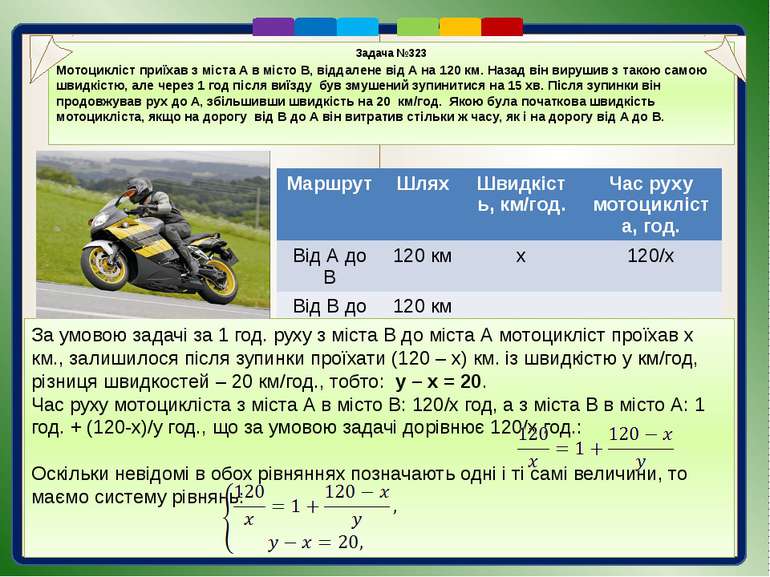
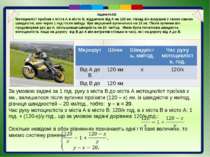
Задача №323 Мотоцикліст приїхав з міста А в місто В, віддалене від А на 120 км. Назад він вирушив з такою самою швидкістю, але через 1 год після виїзду був змушений зупинитися на 15 хв. Після зупинки він продовжував рух до А, збільшивши швидкість на 20 км/год. Якою була початкова швидкість мотоцикліста, якщо на дорогу від В до А він витратив стільки ж часу, як і на дорогу від А до В. За умовою задачі за 1 год. руху з міста В до міста А мотоцикліст проїхав х км., залишилося після зупинки проїхати (120 – х) км. із швидкістю у км/год, різниця швидкостей – 20 км/год., тобто: у – х = 20. Час руху мотоцикліста з міста А в місто В: 120/х год, а з міста В в місто А: 1 год. + (120-х)/у год., що за умовою задачі дорівнює 120/х год.: Оскільки невідомі в обох рівняннях позначають одні і ті самі величини, то маємо систему рівнянь: Маршрут Шлях Швидкість, км/год. Час руху мотоцикліста, год. Від А до В 120 км х 120/х Від В до А 120 км

Задача №318 Задача №318 Один оператор набирає на комп'ютері за годину на 2 сторінки більше ніж другий, а обидва мали набрати по 80 сторінок. Скільки сторінок набрав за годину кожен оператор, якщо разом на всю роботу вони витратили 18 год.

Задача №320 Задача №320 Відстань між двома залізничними станціями дорівнює 96 км. Швидкий поїзд долає її на 2/3 год. швидше, ніж пасажирський. Знайдіть швидкість кожного поїзда, якщо відомо, що різниця швидкостей поїздів дорівнює 12 км/год.

Задача №323 Задача №323 Мотоцикліст приїхав з міста А в місто В, віддалене від А на 120 км. Назад він вирушив з такою самою швидкістю, але через 1 год після виїзду був змушений зупинитися на 15 хв. Після зупинки він продовжував рух до А, збільшивши швидкість на 20 км/год. Якою була початкова швидкість мотоцикліста, якщо на дорогу від В до А він витратив стільки ж часу, як і на дорогу від А до В.