Презентація на тему:
Задачі на відсоткові розрахунки

Тема 5 Елементи прикладної математики Математичне моделювання Відсоткові розрахунки. Поняття про теорію імовірностей. Основні поняття теорії імовірностей. Ймовірність випадкової події Початкові відомості про математичну статистику. Статистичні дані. Способи подання даних Середнє значення. Розв'язування вправ

Пункт 7.2. Пригадайте 1). Що називають відсотком? 2). Як записати певну кількість відсотків у вигляді десяткового дробу? Наведіть приклади 3). Як записати у відсотках десятковий дріб? Наведіть приклади 4). Як знайти відсоток від числа? Наведіть приклади 5). Як знайти число за його відсотком? Наведіть приклади 6). Що таке відсоткове відношення двох чисел? Наведіть приклади Відсоткові розрахунки Основні задачі на відсотки Задачі на прості відсотки Задачі на складні відсотки

Пункт 7.2. Основні задачі на відсотки

Пункт 7.2. Основні задачі на відсотки Розглянемо прикладні задачі четвертого типу. У процесі їх розв'язування використовують спеціальні назви величин:

Пункт 7.2. Основні задачі на відсотки Задача 1. Щомісячна оплата за радіо становить 4 грн. Абонент прострочив оплату на 25 днів. Яку суму він має сплатити, якщо за кожний прострочений день нараховується пеня у розмірі 1% від суми щомісячної оплати? Розв'язання. Відсоткові гроші становлять: Загальна сума (нарощене число) оплати через 25 днів разом з пенею становить:

Пункт 7.2. Основні задачі на відсотки Розв'язання. Відсоткові гроші за перший рік становитимуть Нарощений капітал через рік становитиме 600+600 0,16 = 600 (1+0,16)= =600 1,16 (грн.) Відсоткові гроші за другий рік становитимуть: Нарощений капітал через два роки становитиме: Задача 2. У банк, що виплачує 16% річних, покладено 600грн. В яку суму перетвориться цей вклад через 2 роки?

Пункт 7.2. Основні задачі на відсотки В першій задачі відсоток пені за кожен прострочений день нараховується від початкової суми 4 грн., і тому пеня за кожен день не змінюється, а в другій — річний прибуток з кожним роком збільшується, бо нараховується з нарощеного капіталу, сума якого з кожним роком зростає. Відсоткові розрахунки, проведені в другій задачі, називають складними відсотками на відміну від простих відсотків (перша задача). Складними відсотками, як правило, користуються під час фінансових розрахунків, а також розв'язуючи задачі, пов'язані з підрахунками народонаселення, визначенням кількісних змін у рослинному та тваринному світі тощо. Величини, що використовуються в таких задачах, зокрема у фінансових розрахунках, позначають так: початковий капітал — а0 , відсоткова такса —р%, час обігу грошей у банку — t, відсоткові гроші Pt , нарощений капітал — Аt

Пункт 7.2. Задачі на прості відсотки Якщо приріст капіталу або зміна чогось іншого обраховується за простими відсотками, то, використовуючи введені позначення, можемо обчислити нарощений капітал At через t років після внесення вкладу. Якщо відсоткова такса становить р%, то за рік початковий капітал а0 зросте на суму грошових одиниць, а за t років — на грошових одиниць. Нарощений капітал можна обчислити за формулою або

Пункт 7.2. Задачі на прості відсотки Розв'язання. Оскільки в даному випадку річна такса розраховується з початкового капіталу (позиченої суми), то тут маємо справу з простими відсотками. За умовою: Аt = 18750, а0= 10000, р=25%. Підставляючи ці дані у формулу (1), маємо: Звідси 18750 = 10000 + 2500t; 2500t = 8750; t = 3,5. Отже, позику було надано на 3,5 роки. Задача 3. На який термін банк надав позику в розмірі 10000 грн., якщо, повертаючи кредит, позичальник сплатив 18750 грн., а річна такса становила 25%?

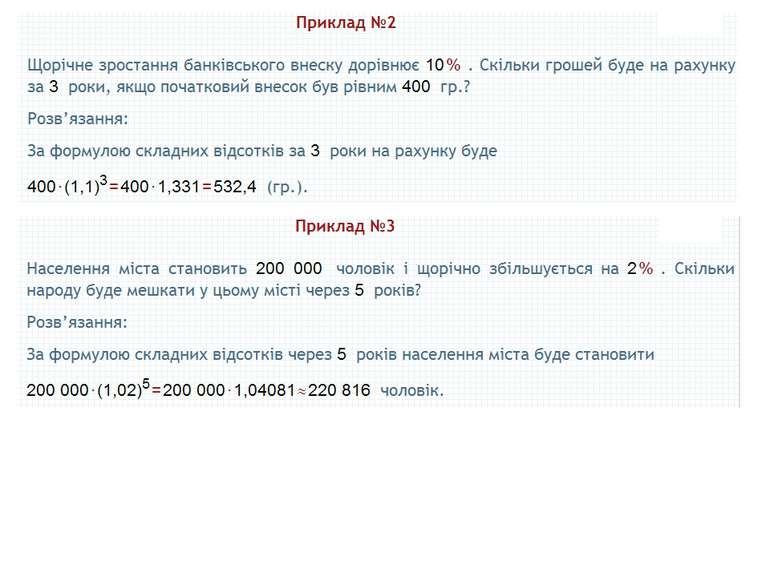
Пункт 7.2. Задачі на складні відсотки Нехай початковий капітал становить а0 грошових одиниць, а відсоткова такса дорівнює р%. За перший рік початковий капітал зросте на р%, тобто на грошових одиниць, і через рік нарощений капітал становитиме грошових одиниць. За другий рік відсоткові гроші нараховуватимуться вже від нарощеного капіталу А1 і становитимуть грошових одиниць, а нарощений капітал, після другого року дорівнюватиме: Встановимо формулу обчислення нарощеного капіталу, якщо відсоткова такса нараховується з нарощеного капіталу (складні відсотки).

Пункт 7.2. Задачі на складні відсотки Встановимо формулу обчислення нарощеного капіталу, якщо відсоткова такса нараховується з нарощеного капіталу (складні відсотки). Аналогічно через t років: формула (2)

Пункт 7.2. Задачі на складні відсотки Розв'язання. Оскільки розрахунок зростання продуктивності праці щороку здійснюється з урахуванням уже нарощеної продуктивності, то в даному випадку маємо справу із складними відсотками. Нехай початкова продуктивність праці на заводі дорівнює а0 і щороку збільшується на р%. Тоді за формулою (2) продуктивність праці в кінці третього року А3 становитиме З іншого боку, відповідно до умови задачі, продуктивність праці зросла на 33,1%, тобто в 1,331 рази і становить: а0 1,331 = 1,331а0. Маємо рівняння: Задача 4. Продуктивність праці на заводі щороку збільшується на однакову кількість відсотків. За три роки вона зросла на 33,1%. На скільки відсотків щороку збільшувалася продуктивність праці? Отже, щороку продуктивність праці на заводі зростала на 10%.

Первинне закріплення вивченого матеріалу