Презентація на тему:
Сума перших n членів арифметичної прогресії

Тема 6 Арифметична та геометрична прогресії Числові послідовності. Властивості числових послідовностей Арифметична прогресія. Формула n-го члена арифметичної прогресії Сума перших n членів арифметичної прогресії Геометрична прогресія. Формула n-го члена геометричної прогресії Сума перших n членів геометричної прогресії Нескінченна геометрична прогресія (|q| < 0) та її сума Розв’язування вправ

Пункт 10.3. Як рахував Гаусс. Розповідають, що незвичайні здібності видатного німецького математика Карла Фрідріха Гаусса (1777-1855) почали виявлятися вже в ранньому віці. Якось він здивував учителя, миттєво обчисливши суму перших ста натуральних чисел. Він, очевидно, помітив, що в послідовності 1; 2; 3; 4; ...; 97; 98; 99; 100 сума першого і останнього числа дорівнює 101 (1 + 100 = 101), другого і передостаннього — теж 101 (2 + 99 = 101), третього від початку і третього від кінця — теж 101 (3 + 98 = 101) і т.д. Всього таких сум можна утворити 50 (остання — 50 + 51). Отже, сума перших ста натуральних чисел дорівнює 101 • 50 = 5050. Сума перших n членів арифметичної прогресії Пригадайте 1). Який вигляд має формула загального члена арифметичної прогресії? 2). Як виразити через а1 і d член арифметичної прогресії, номер якого дорівнює n-k?

Карл Гаус ( 1777 – 1855 ) Німецький математик, астроном, геодезист, фізик, вважається «королем математики». «Математика – цариця всіх наук, арифметика – цариця математики» Народився 30 квітня 1777 року в герцогстві Брауншвейг у сім’ї садівника. Видатні математичні здібності проявив вже у ранньому дитинстві. Німеччина

Доведення Нехай маємо скінченну арифметичну прогресію a1 , a2, a3, …, an-2 , an-1 , an . Запишемо у загальному вигляді два довільні члени прогресії, які рівновіддалені від її крайніх членів, наприклад, стоять на на k-му місці від початку і від кінця. На k- му місці від початку прогресії знаходиться член ak . Тепер встановимо номер члена, який стоїть на k-мy місці від кінця прогресії. Перед цим зауважимо, що сума номерів крайніх членів і членів, рівновіддалених від крайніх, на 1 більша від кількості n членів прогресії і дорівнює n + 1. a1 , a2, a3, …, an-2 , an-1 , an Властивість арифметичної прогресії ak + an-k+l = a1 + an. Послідовність перших ста натуральних чисел є скінченною арифметичною прогресією, перший і останній члени (або інакше, крайні члени) якої дорівнюють відповідно 1 і 100, а різниця d = 1. Вона має властивість, яку і помітив Гаусс: сума будь-яких двох її членів, рівновіддалених від крайніх членів, дорівнює сумі крайніх членів (у даному випадку 101)

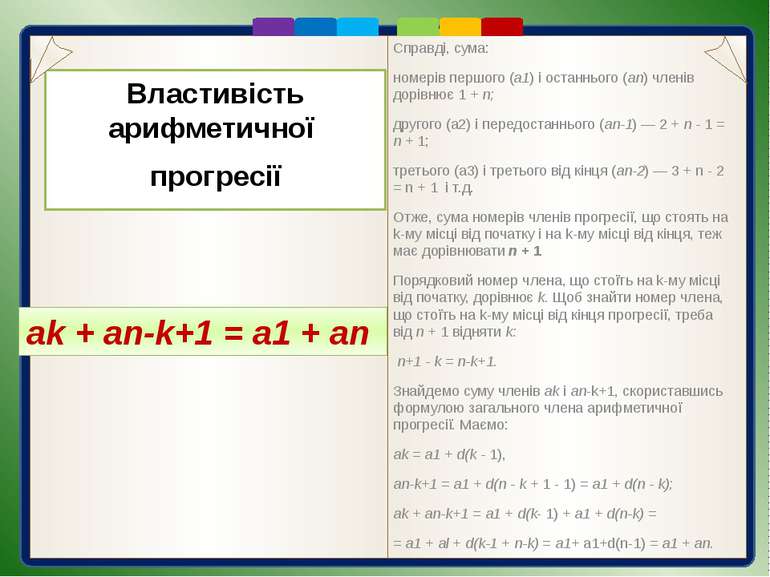
Справді, сума: номерів першого (a1) і останнього (an) членів дорівнює 1 + n; другого (а2) і передостаннього (an-1) — 2 + n - 1 = n + 1; третього (а3) і третього від кінця (an-2) — 3 + n - 2 = n + 1 і т.д. Отже, сума номерів членів прогресії, що стоять на k-му місці від початку і на k-му місці від кінця, теж має дорівнювати n + 1 Порядковий номер члена, що стоїть на k-му місці від початку, дорівнює k. Щоб знайти номер члена, що стоїть на k-му місці від кінця прогресії, треба від n + 1 відняти k: n+1 - k = n-k+1. Знайдемо суму членів ak і аn-k+1, скориставшись формулою загального члена арифметичної прогресії. Маємо: ak = a1 + d(k - 1), аn-k+1 = а1 + d(n - k + 1 - 1) = a1 + d(n - k); ak + an-k+1 = a1 + d(k- 1) + a1 + d(n-k) = = a1 + al + d(k-1 + n-k) = a1+ а1+d(n-1) = a1 + an. Властивість арифметичної прогресії ak + an-k+1 = a1 + an

Доведену властивість можна використати для встановлення формули обчислення суми n перших членів арифметичної прогресії. Нехай треба знайти суму членів арифметичної прогресії: a1 , a2, a3, …, an-2 , an-1 , an . Позначають таку суму зазвичай Sn. Запишемо цю суму двома способами: у прямому і зворотному порядку розміщення доданків. Маємо: Sn = a1 + a2+ a3+ …+ an-2 + an-1 + an . Sn = an + an-1 + an-2+... + a3 + a2 + a1, Додамо почленно ці дві рівності. Маємо: 2 Sn = (а1 + аn) + (a2 + аn-1) + (a3 + an-2)+ ... +(an-2 + a3)+ (аn-1 + a2 )+(аn + а1). За доведеною властивістю кожна із сум у дужках дорівнює а1 + аn Кількість таких сум дорівнює n. Отже, 2Sn = (а1 + аn)n. Звідси: Формула суми перших n членів арифметичної прогресії

Враховуючи те, що аn = а1 +d(n - 1), формулу суми членів арифметичної прогресії можна записати і в такому вигляді: За встановленою формулою суму ста перших натуральних чисел можна обчислити так: Формула суми перших n членів арифметичної прогресії

Яку властивість скінченної арифметичної прогресії використовують для встановлення формули суми n перших її членів? Запишіть у зошиті два варіанти формули суми n перших членів арифметичної прогресії. В якому випадку, на ваш погляд, доцільніше використовувати один з них, а в якому випадку — інший? Запитання для самоперевірки

Первинне закріплення вивченого матеріалу 1. В послідовності (хn): 3; 0; -3; -6; -9; -12;... вкажіть перший, третій і шостий члени. Усні вправи 2. Послідовність (аn) задана формулою аn = 6n - 1. Знайдіть a1, а2, a3 ; а20, а100, аk.

Первинне закріплення вивченого матеріалу 3. Назвіть п’ять перших членів послідовності (сn), якщо: с1 = 32; сn+1 = 0,5сn Усні вправи 4. Продовжіть дану послідовність: а)1; 5; 9; 13; 17; … б)1; 5; 9; 13; 17; 21; 25; 29; 33;… 32;16; 8; 4; 2; …

Первинне закріплення вивченого матеріалу 5. Відомо, що а1 = 1, d = 1. Задайте цю прогресію Усні вправи 6. Відомо, що а1 = 1, d = 2. Задайте цю прогресію

Первинне закріплення вивченого матеріалу 7. Послідовність(аn) – арифметична прогресія, в якій а1 = 4; d = 2. Знайдіть 50-ий член цієї прогресії. Усні вправи

Первинне закріплення вивченого матеріалу Усні вправи 8. Бригада стіклодувів виготовила в січні 80 виробів, а кожного наступного місяця виготовляла на 17 виробів більше, ніж за попередній. Скільки виробів виготовила бригада в червні?

1. Дайте означення арифметичної прогресії. Відповідь: Арифметичною прогресією називається числова послідовність, кожний член якої, начинаючи з другого, дорівнює попередньому, до якого додається одне й те ж число.

2. Що називають різницею арифметичної прогресії? Як позначають? Відповідь: це число, яке показує на скільки кожний наступний член більший або менший попереднього. Позначають буквою d.

3. Назвати формулу n-ого члена арифметичної прогресії.

4. Які властивості арифметичної прогресії? Відповідь: Кожний член арифметичної прогресії, починаючи з другого дорівнює середньому арифметичному двох сусідніх з ним членів.

4. Які властивості арифметичної прогресії? Відповідь: Сума будь-яких двох членів скінченної арифметичної прогресії, які рівновіддалені від її крайніх членів, дорівнює сумі крайніх членів цієї прогресії.

6. Які бувають арифметичні прогресії? Відповідь: Якщо в арифметичній прогресії різниця d > 0, то прогресія є зростаючою. Якщо в арифметичній прогресії різниця d

Які із послідовностей є арифметичними прогресіями? 3, 6, 9, 12,….. 5, 12, 18, 24, 30,….. 7, 14, 28, 35, 49,…. 5, 15, 25,….,95…. 1000, 1001, 1002, 1003,…. 1, 2, 4, 7, 9, 11….. 5, 4, 3, 2, 1, 0, -1, -2,…. Перевір себе! d = 3 d = 10 d = 1 d = - 1

Знайти різницю арифметичної прогресії: 1; 5; 9……… 105; 100…. -13; -15; -17…… 11; ; 19,…. Обчисли усно!

1. В арифметичній прогресії 2,4; 2,6;… різниця дорівнює 2. 2. Четвертий член арифметичної прогресії 0,3; 0,7; 1,1,… дорівнює 1,5 3. 11-ий член арифметичної прогресії, для якої дорівнює 0,2 Істинне чи хибне твердження

Між числами 6 і 21 вставте 4 числа так, щоб разом з даними числами вони утворили арифметичну прогресію. Розв’язання: = 6, = 21, d = (21 – 6)/ (6 – 1)= 3, 6, 9, 12, 15, 18, 21. Здогадайся:

Формула суми n перших членів арифметичної прогресії. Висновок