Презентація на тему:
Розділ Комбінаторика

Комбінаторика

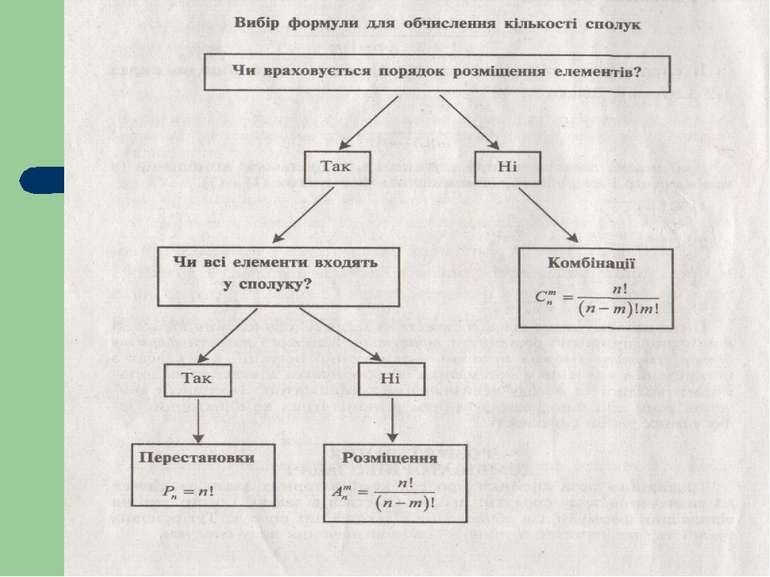
Розв’язування простих комбінаторних задач зводиться до визначення виду сполуки, про яку йдеться в задачі, і застосування відповідної формули для обчислення кількості цих сполук

схема

Зроби правильний вибір формули Скількома способами можна: А) встановити порядок заїзду в групі із 12 спортсменів-саночників? Б) присудити золоту, срібну і бронзову медалі на змаганнях, в яких бере участь 15 атлетів? В) із 14 спортсменів вибрати чотири учасника естафети?

Комбінаторні задачі бувають різних видів. Але більшість із них розв’язують за допомогою двох основних правил: правила суми і правила добутку Правило суми (або А, або Б) : Якщо деякий об’єкт А можна вибрати m способами, а об’єкт Б – іншими n способами, причому вибори об’єктів А і Б несумісні, то вибір «або А, або Б» можна здійснити m+n способами. Правило добутку (і А, і Б) : Якщо деякий об’єкт А можна вибрати m способами, і після кожного такого вибору інший об’єкт Б можна вибрати (незалежно від вибору об’єкта А) n способами , то пари об’єктів А і Б можна вибрати m∙n способами.

Задачі Скільки існує п’ятицифрових непарних чисел, складених з цифр 2, 4, 6, 8, 9 в яких цифри не повторюються? Скільки різних дільників має число 2310? У шаховому гуртку 5 хлопців і 3 дівчини. Для зустрічі з гросмейстером прийшло три запрошення. Скількома способами можна розподілити запрошення так, щоб на зустріч потрапила хоча б одна дівчина? В речовій лотереї розігрується 8 предметів. Всього в «урні» 50 квитків. Виймається 5 квитків. Скількома способами їх можна витягнути так, щоб: А) рівно два з них було виграшних; Б) принаймні два з них були виграшні

Застосування рівнянь при роз'вязуванні комбінаторних задач У 9-А класі учнів на два більше, ніж в 9-Б. Відомо, що кількість способів вибору старости і його заступника в 9-А класі на 82 більше, ніж в 9-Б. Скільки учнів вчаться в кожному класі? Декілька фахівців претендують на посади тренера збірної, його помічника і начальника команди. Скільки претендентів на ці посади, якщо скласти вищеназвану трійку можна 336 способами?

Бажаємо успіхів