Презентація на тему:
Поділ відрізка навпіл. Побудова перпендикулярної прямої

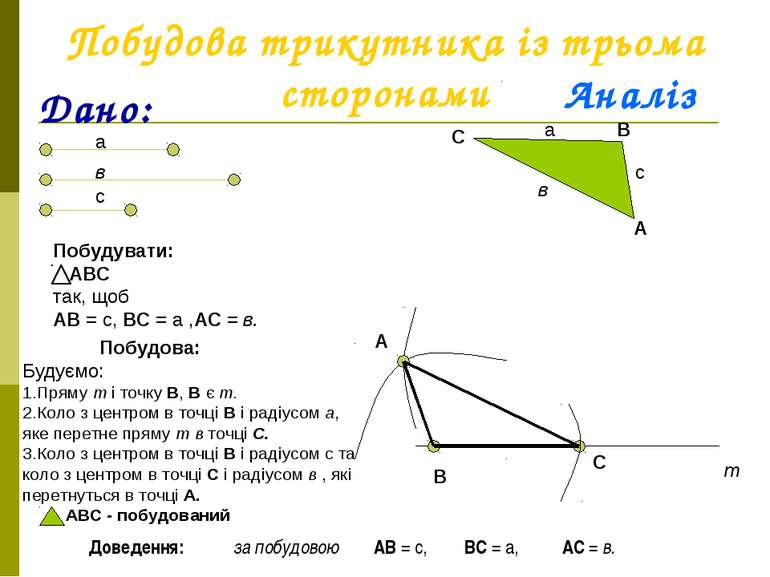
Побудова трикутника із трьома сторонами Дано: а в с Побудувати: АВС так, щоб АВ = с, ВС = а ,АС = в. А В С с а в Побудова: Будуємо: 1.Пряму т і точку В, В є т. 2.Коло з центром в точці В і радіусом а, яке перетне пряму т в точці С. 3.Коло з центром в точці В і радіусом с та коло з центром в точці С і радіусом в , які перетнуться в точці А. АВС - побудований т В С А Аналіз Доведення: за побудовою АВ = с, ВС = а, АС = в.

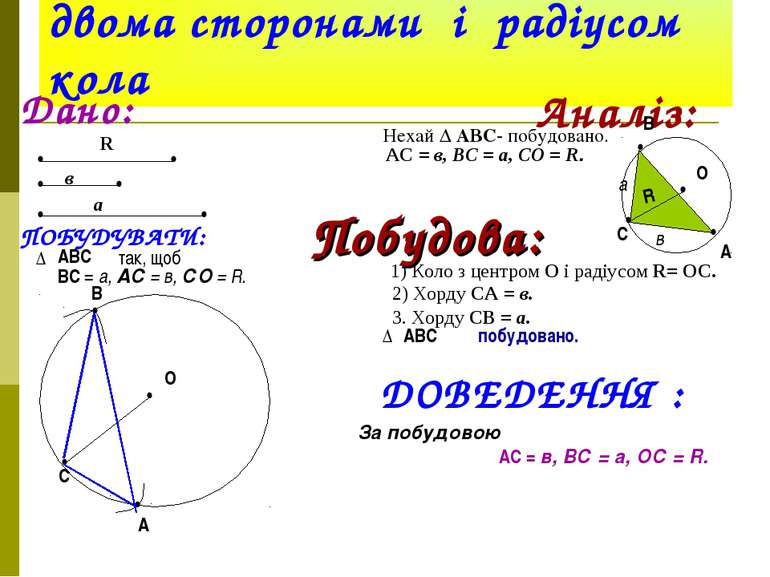
Побудова трикутника за двома сторонами і радіусом кола Дано: • • • • • • R в а ПОБУДУВАТИ: ∆ АВС так, щоб ВС = а, АС = в, СО = R. Аналіз: Нехай ∆ АВС- побудовано. • • • • АС = в, ВС = а, СО = R. А В С О а в R Побудова: 1) Коло з центром О і радіусом R= ОС. • О • С 2) Хорду СА = в. • А 3. Хорду СВ = а. • В побудовано. ДОВЕДЕННЯ : За побудовою АС = в, ВС = а, ОС = R. ∆ АВС

Побудова кута, рівного даному куту Дано: АВС А В С Побудувати: В1ОС1 = ВАС ПОБУДОВА: 1.Будуємо пряму т і точку О, О є т. т ● О 2. Довільне коло з центром в точці А даного кута. В і С – точки перетину цього кола зі сторонами кута. ● ● 3. Радіусом АВ проведемо коло з центром в точці О , В1- точка перетину з прямою т. ● В1 4. Радіусом ВС з центром в точці В1 опишем коло. С1- точка перетину двох кіл. ● С1 В1ОС1 = ВАС Доведення: ВАС = В1ОС1 за трьома сторонами (АВ=ОВ; АС=ОС1;СВ=В1С1 за побудовою). Кути ВАС і В1ОС1- відповідні, отже ВАС = В1ОС1 що й треба було довести

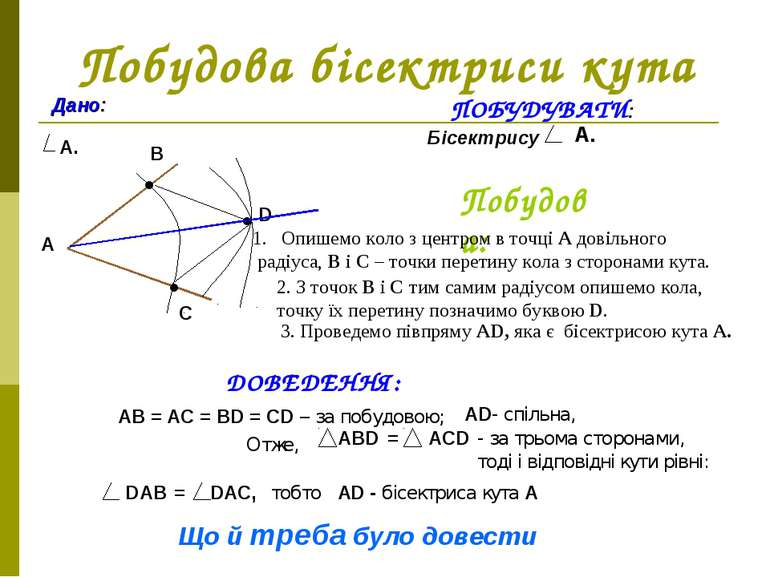
Побудова бісектриси кута Дано: А. А ПОБУДУВАТИ: Бісектрису А. Побудова: Опишемо коло з центром в точці А довільного радіуса, В і С – точки перетину кола з сторонами кута. ● ● В С 2. З точок В і С тим самим радіусом опишемо кола, точку їх перетину позначимо буквою D. ● D 3. Проведемо півпряму АD, яка є бісектрисою кута А. ДОВЕДЕННЯ: АВ = АС = ВD = СD – за побудовою; АD- спільна, Отже, АВD = АСD - за трьома сторонами, тоді і відповідні кути рівні: DАВ = DАС, тобто АD - бісектриса кута А Що й треба було довести

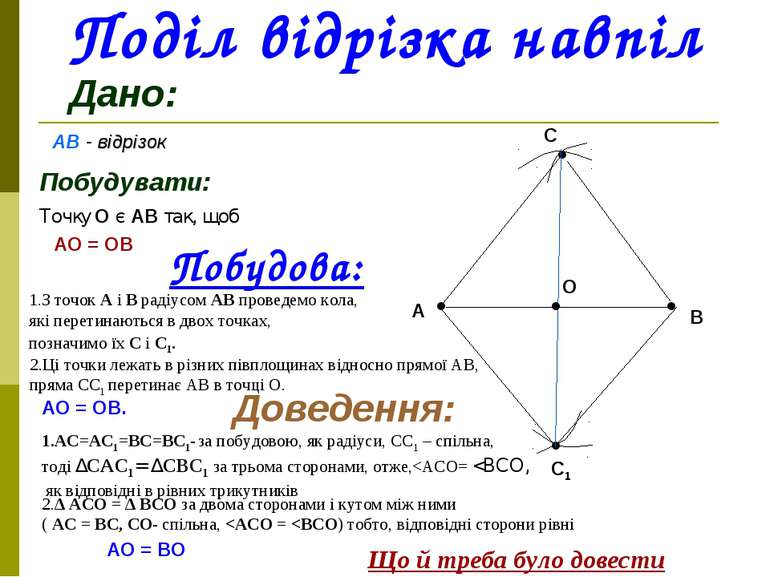
Поділ відрізка навпіл Дано: АВ - відрізок ● ● А В Побудувати: Точку О є АВ так, щоб АО = ОВ Побудова: 1.З точок А і В радіусом АВ проведемо кола, які перетинаються в двох точках, позначимо їх С і С1. ● ● С С1 2.Ці точки лежать в різних півплощинах відносно прямої АВ, пряма СС1 перетинає АВ в точці О. ● О АО = ОВ. Доведення: 1.АС=АС1=ВС=ВС1- за побудовою, як радіуси, СС1 – спільна, тоді ∆САС1= ∆СВС1 за трьома сторонами, отже,

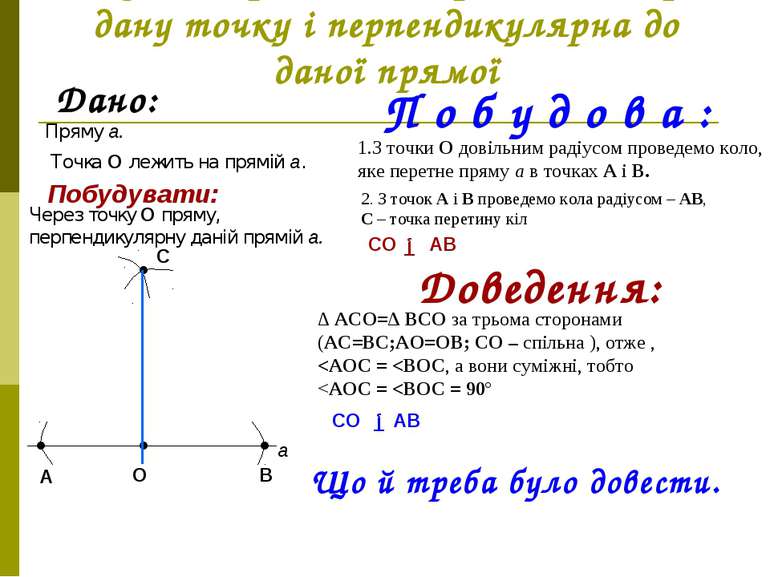
Побудова прямої, що проходить через дану точку і перпендикулярна до даної прямої Дано: Точка О лежить на прямій а. Пряму а. а ● О Побудувати: Через точку О пряму, перпендикулярну даній прямій а. П о б у д о в а : 1.З точки О довільним радіусом проведемо коло, яке перетне пряму а в точках А і В. ● ● А В 2. З точок А і В проведемо кола радіусом – АВ, С – точка перетину кіл ● С СО Ţ АВ Доведення: ∆ АСО=∆ ВСО за трьома сторонами (АС=ВС;АО=ОВ; СО – спільна ), отже ,

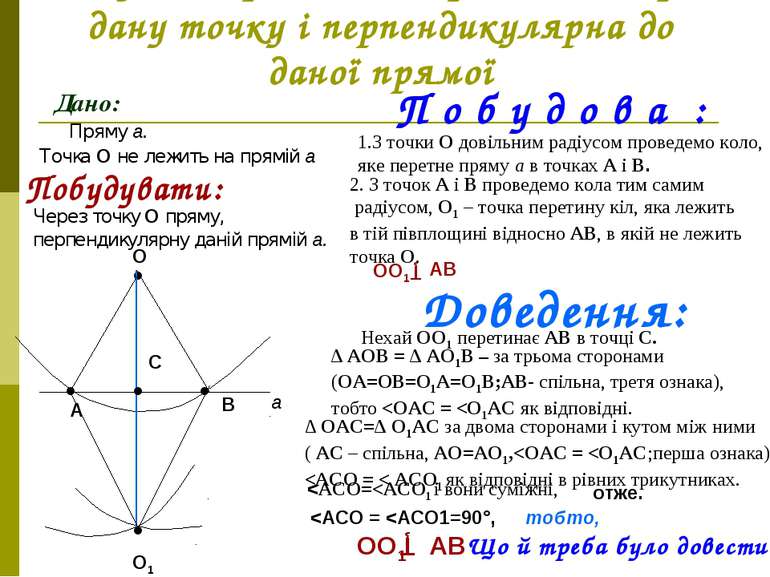
Побудова прямої, що проходить через дану точку і перпендикулярна до даної прямої Дано: Пряму а. Точка О не лежить на прямій а Побудувати: Через точку О пряму, перпендикулярну даній прямій а. а ● О П о б у д о в а : 1.З точки О довільним радіусом проведемо коло, яке перетне пряму а в точках А і В. ● ● А В 2. З точок А і В проведемо кола тим самим радіусом, О1 – точка перетину кіл, яка лежить в тій півплощині відносно АВ, в якій не лежить точка О. ● О1 ОО1 Ţ АВ Доведення: Нехай ОО1 перетинає АВ в точці С. ● С ∆ АОВ = ∆ АО1В – за трьома сторонами (ОА=ОВ=О1А=О1В;АВ- спільна, третя ознака), тобто

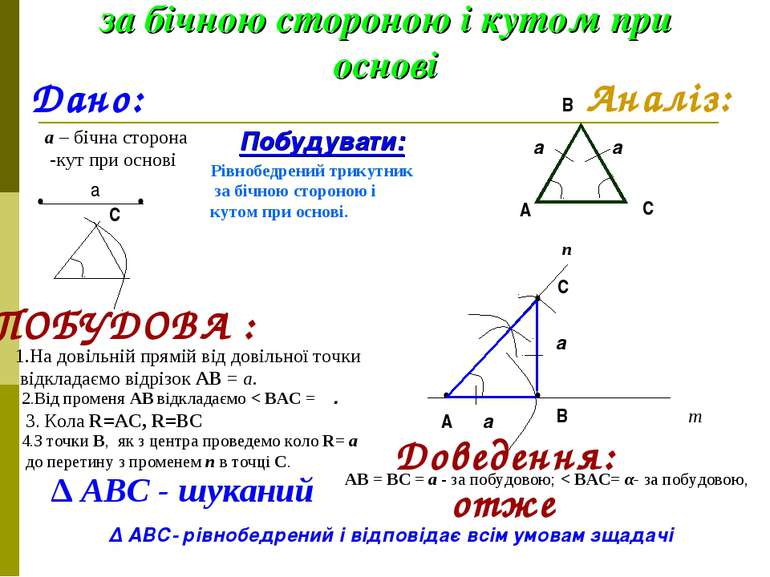
Побудова рівнобедреного трикутника за бічною стороною і кутом при основі Дано: а – бічна сторона α-кут при основі • • а α Аналіз: А В С а а α ПОБУДОВА : Побудувати: Рівнобедрений трикутник за бічною стороною і кутом при основі. 1.На довільній прямій від довільної точки відкладаємо відрізок АВ = а. т • А • В 2.Від променя АВ відкладаємо < ВАС = α. С 3. Кола R=АС, R=ВC 4.З точки В, як з центра проведемо коло R= а до перетину з променем п в точці С. п • С ∆ АВС - шуканий Доведення: АВ = ВС = а - за побудовою; < ВАС= α- за побудовою, а а α отже ∆ АВС- рівнобедрений і відповідає всім умовам зщадачі