Презентація на тему:
планаметричні задачі

Розв'язування планіметричних задач на побудову

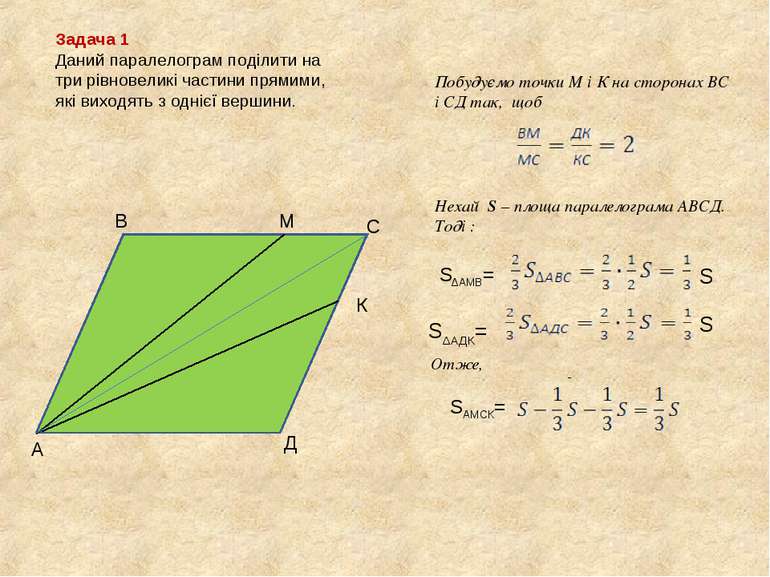
Задача 1 Даний паралелограм поділити на три рівновеликі частини прямими, які виходять з однієї вершини. А В С Д Побудуємо точки М і К на сторонах ВС і СД так, щоб Нехай S – площа паралелограма АВСД. Тоді : S∆АДК= S S - М К S∆АМВ= Отже, SАМСК=

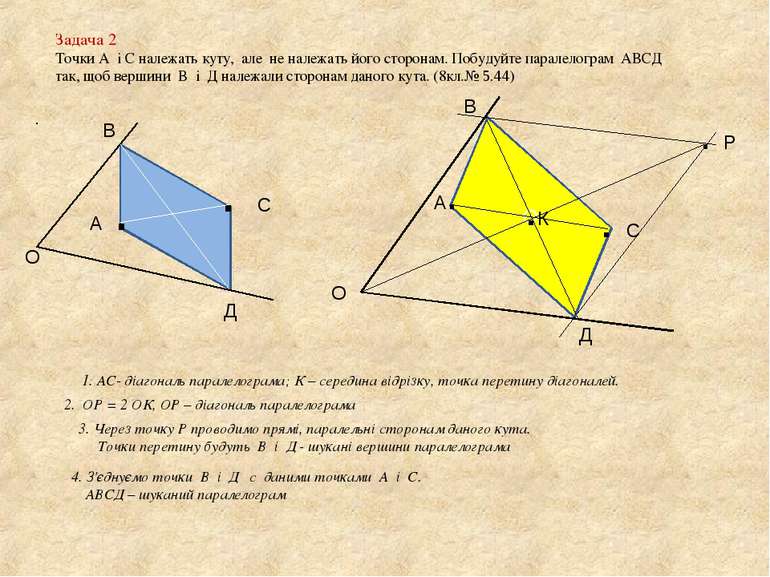
Задача 2 Точки А і С належать куту, але не належать його сторонам. Побудуйте паралелограм АВСД так, щоб вершини В і Д належали сторонам даного кута. (8кл.№ 5.44) А . . С В Д О О О А. . С .К . Р В Д 1. АС- діагональ паралелограма; К – середина відрізку, точка перетину діагоналей. 2. ОР = 2 ОК, ОР – діагональ паралелограма 3. Через точку Р проводимо прямі, паралельні сторонам даного кута. Точки перетину будуть В і Д - шукані вершини паралелограма 4. З'єднуємо точки В і Д с даними точками А і С. АВСД – шуканий паралелограм

Задача 3 Побудуйте трапецію за основами і бічними сторонами (8кл.№10.36) с а в d c а - в А Д К С В АД = а 2. Коло с центром в А і радіусом ВС = в; точка перетину - К 3. Базисний трикутник КСД, за трьома сторонами. Вершина С, сторона СД. 4. Коло з центром в С і радіусом ВС = в, коло з центром в А і радіусом АВ = с. Точка перетину – вершина В 5. Відрізки ВС і АВ, АВСД - трапеція А В С Д

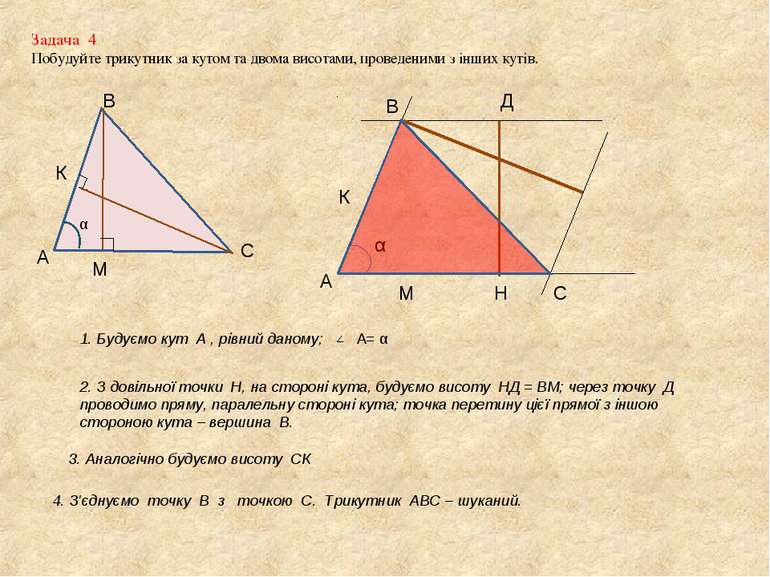
Задача 4 Побудуйте трикутник за кутом та двома висотами, проведеними з інших кутів. А В С К М α А В Н С 1. Будуємо кут А , рівний даному; А= α α Д 2. З довільної точки Н, на стороні кута, будуємо висоту НД = ВМ; через точку Д проводимо пряму, паралельну стороні кута; точка перетину цієї прямої з іншою стороною кута – вершина В. М 3. Аналогічно будуємо висоту СК 4. З'єднуємо точку В з точкою С. Трикутник АВС – шуканий. К

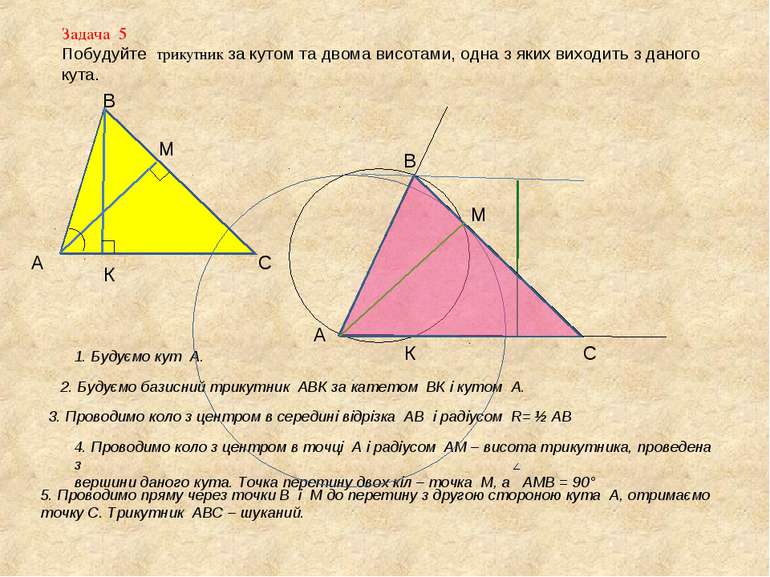
Задача 5 Побудуйте трикутник за кутом та двома висотами, одна з яких виходить з даного кута. А В С К М 1. Будуємо кут А. А 2. Будуємо базисний трикутник АВК за катетом ВК і кутом А. В К 3. Проводимо коло з центром в середині відрізка АВ і радіусом R= ½ АВ 4. Проводимо коло з центром в точці А і радіусом АМ – висота трикутника, проведена з вершини даного кута. Точка перетину двох кіл – точка М, а АМВ = 90° М 5. Проводимо пряму через точки В і М до перетину з другою стороною кута А, отримаємо точку С. Трикутник АВС – шуканий. С

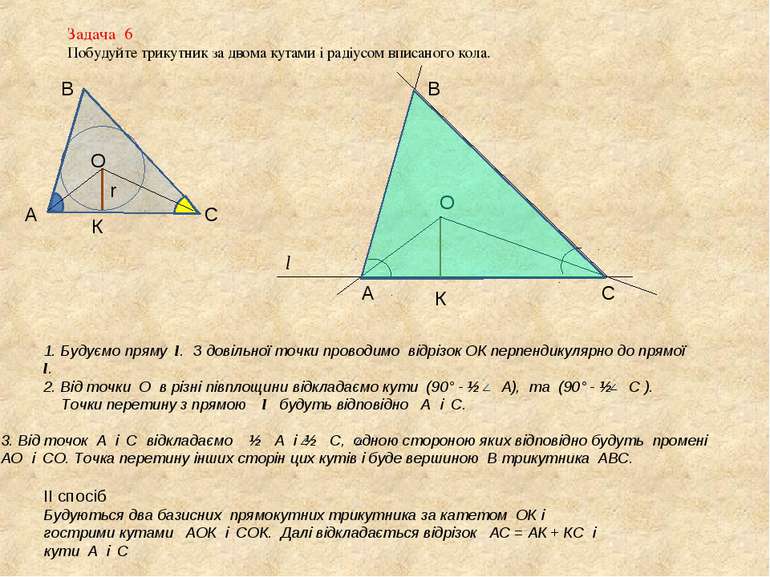
Задача 6 Побудуйте трикутник за двома кутами і радіусом вписаного кола. А В С r О К О К 1. Будуємо пряму l. З довільної точки проводимо відрізок ОК перпендикулярно до прямої l. l 2. Від точки О в різні півплощини відкладаємо кути (90° - ½ А), та (90° - ½ С ). Точки перетину з прямою l будуть відповідно А і С. А С 3. Від точок А і С відкладаємо ½ А і ½ С, одною стороною яких відповідно будуть прoмені АО і СО. Точка перетину інших сторін цих кутів і буде вершиною В трикутника АВС. В ІІ спосіб Будуються два базисних прямокутних трикутника за катетом ОК і гострими кутами АОК і СОК. Далі відкладається відрізок АС = АК + КС і кути А і С

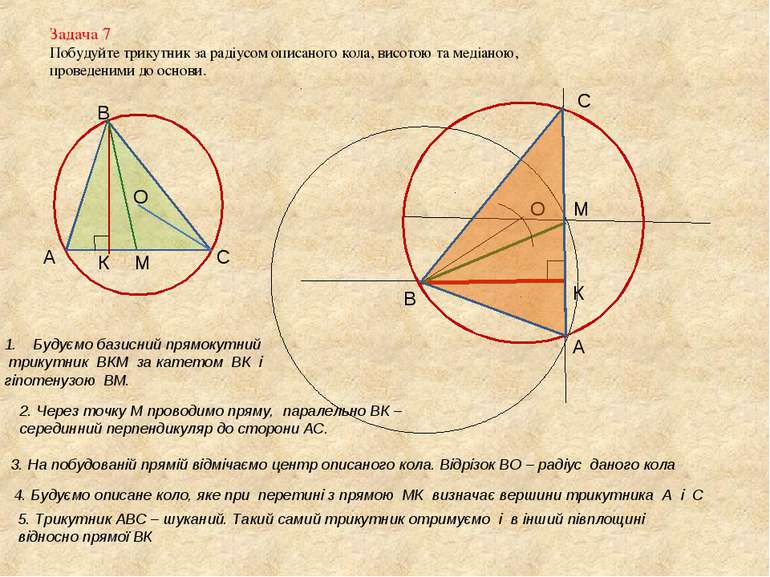
Задача 7 Побудуйте трикутник за радіусом описаного кола, висотою та медіаною, проведеними до основи. А В С О К М Будуємо базисний прямокутний трикутник ВКМ за катетом ВК і гіпотенузою ВМ. В К М 2. Через точку М проводимо пряму, паралельно ВК – серединний перпендикуляр до сторони АС. 3. На побудованій прямій відмічаємо центр описаного кола. Відрізок ВО – радіус даного кола О 4. Будуємо описане коло, яке при перетині з прямою МК визначає вершини трикутника А і С А С 5. Трикутник АВС – шуканий. Такий самий трикутник отримуємо і в інший півплощині відносно прямої ВК

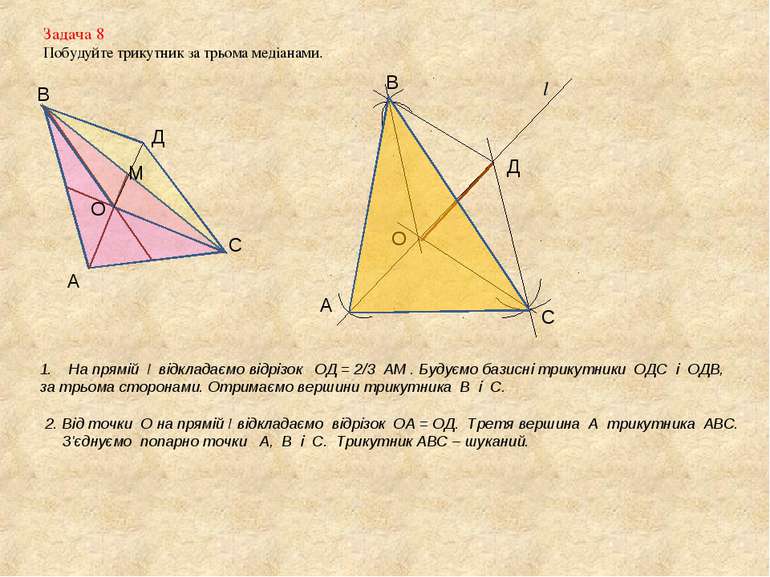
Задача 8 Побудуйте трикутник за трьома медіанами. А В С О Д На прямій l відкладаємо відрізок ОД = 2/3 АМ . Будуємо базисні трикутники ОДС і ОДВ, за трьома сторонами. Отримаємо вершини трикутника В і С. М 2. Від точки О на прямій l відкладаємо відрізок ОА = ОД. Третя вершина А трикутника АВС. З'єднуємо попарно точки А, В і С. Трикутник АВС – шуканий. l О Д С В А

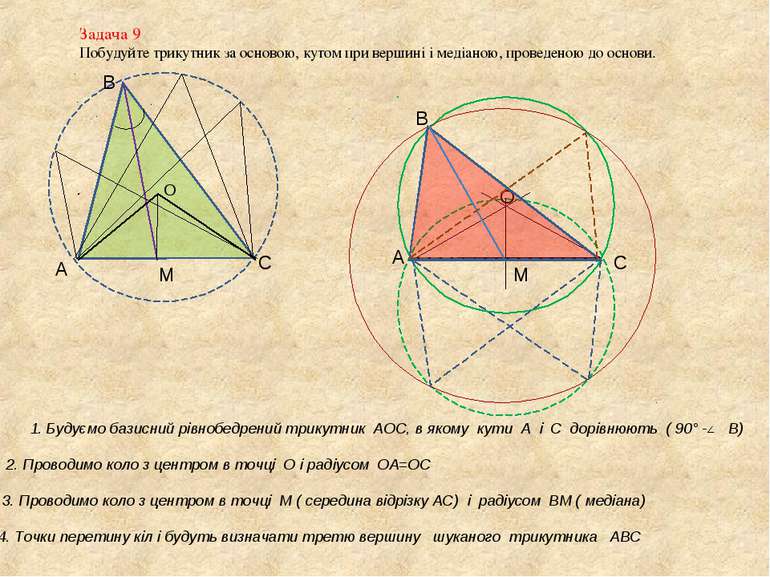
Задача 9 Побудуйте трикутник за основою, кутом при вершині і медіаною, проведеною до основи. А В С М О 1. Будуємо базисний рівнобедрений трикутник АОС, в якому кути А і С дорівнюють ( 90° - В) А С О М 2. Проводимо коло з центром в точці О і радіусом ОА=ОС 3. Проводимо коло з центром в точці М ( середина відрізку АС) і радіусом ВМ ( медіана) 4. Точки перетину кіл і будуть визначати третю вершину шуканого трикутника АВС В

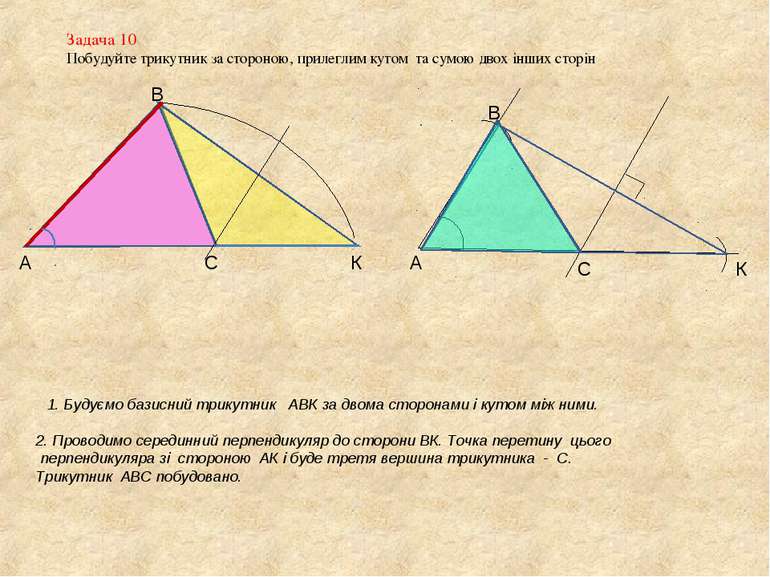
Задача 10 Побудуйте трикутник за стороною, прилеглим кутом та сумою двох інших сторін А В С К 1. Будуємо базисний трикутник АВК за двома сторонами і кутом між ними. А В К 2. Проводимо серединний перпендикуляр до сторони ВК. Точка перетину цього перпендикуляра зі стороною АК і буде третя вершина трикутника - С. Трикутник АВС побудовано. С

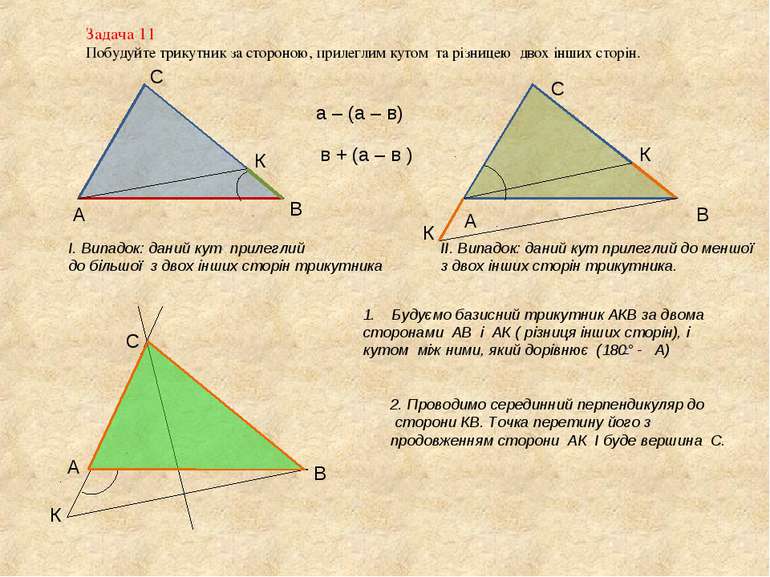
Задача 11 Побудуйте трикутник за стороною, прилеглим кутом та різницею двох інших сторін. А В С І. Випадок: даний кут прилеглий до більшої з двох інших сторін трикутника ІІ. Випадок: даний кут прилеглий до меншої з двох інших сторін трикутника. а – (а – в) К К в + (а – в ) К Будуємо базисний трикутник АКВ за двома сторонами АВ і АК ( різниця інших сторін), і кутом між ними, який дорівнює (180° - А) А В К 2. Проводимо серединний перпендикуляр до сторони КВ. Точка перетину його з продовженням сторони АК І буде вершина С. С

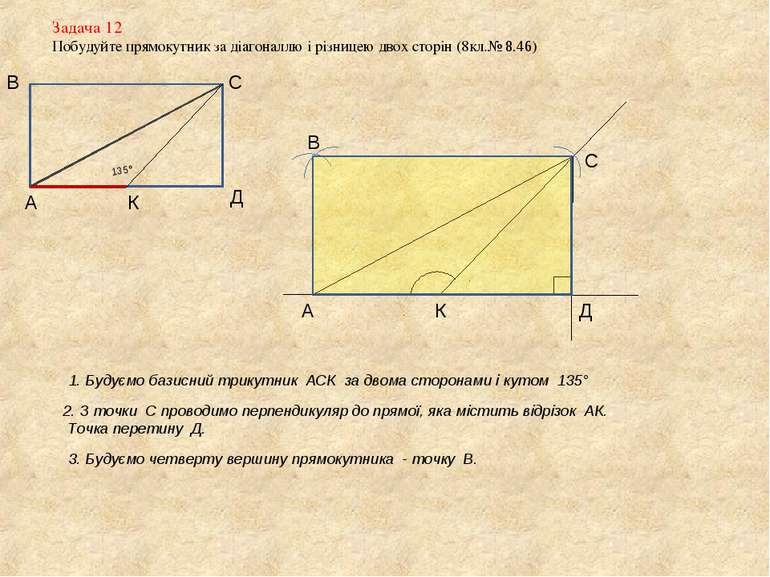
Задача 12 Побудуйте прямокутник за діагоналлю і різницею двох сторін (8кл.№ 8.46) А В С Д К 135° 1. Будуємо базисний трикутник АСК за двома сторонами і кутом 135° А К С 2. З точки С проводимо перпендикуляр до прямої, яка містить відрізок АК. Точка перетину Д. Д 3. Будуємо четверту вершину прямокутника - точку В. В

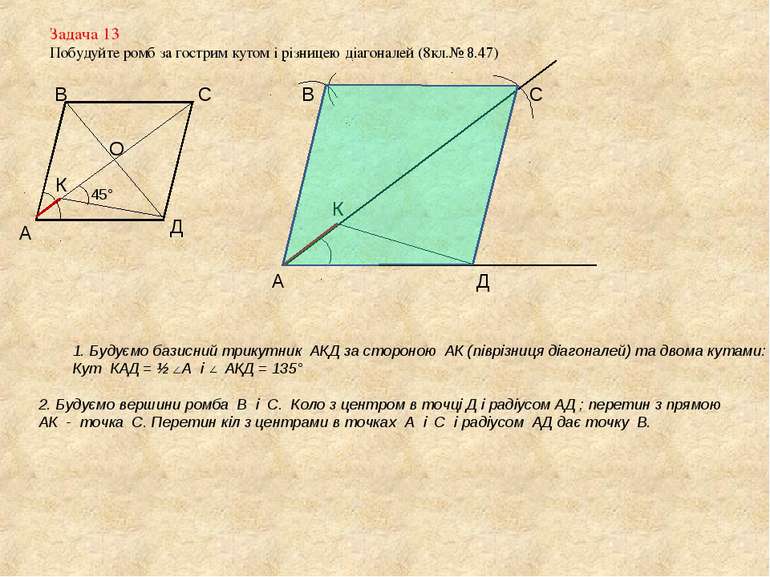
Задача 13 Побудуйте ромб за гострим кутом і різницею діагоналей (8кл.№ 8.47) А В С Д К 45° О 1. Будуємо базисний трикутник АКД за стороною АК (піврізниця діагоналей) та двома кутами: Кут КАД = ½ А і АКД = 135° А Д К 2. Будуємо вершини ромба В і С. Коло з центром в точці Д і радіусом АД ; перетин з прямою АК - точка С. Перетин кіл з центрами в точках А і С і радіусом АД дає точку В. С В

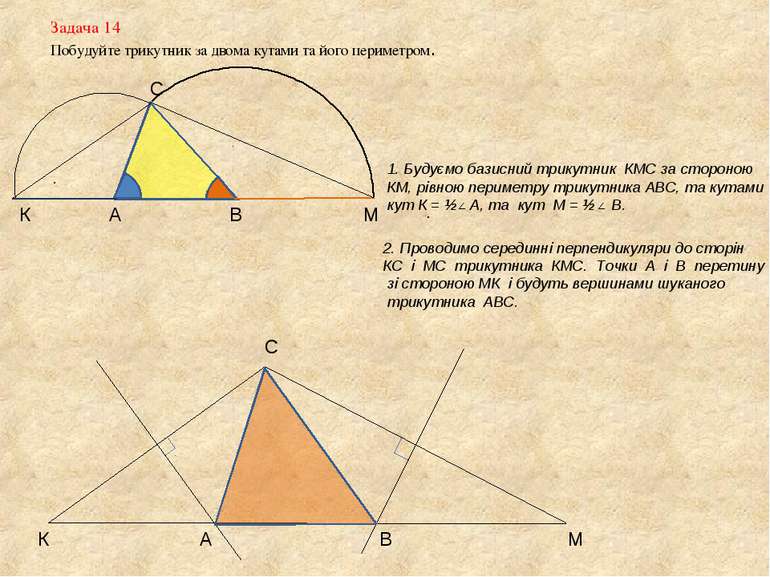
Задача 14 Побудуйте трикутник за двома кутами та його периметром. А В С К М 1. Будуємо базисний трикутник КМС за стороною КМ, рівною периметру трикутника АВС, та кутами кут К = ½ А, та кут М = ½ В. К М С 2. Проводимо серединні перпендикуляри до сторін КС і МС трикутника КМС. Точки А і В перетину зі стороною МК і будуть вершинами шуканого трикутника АВС. А В

Презентацію підготувала Сорокіна Наталія Сергіївна Вчитель математики, спеціаліст вищої кваліфікаційної категорії, старший вчитель. Запорізька гімназія № 107 http://zp107.cc.ua