Презентація на тему:
Розробка модифікованого LS-метода для побудови ймовірнісного висновку в мережах Байєса

Національний технічний університет України “КПІ” ННК “Інститут прикладного системного аналізу” Розробка модифікованого LS-метода для побудови ймовірнісного висновку в мережах Байєса Науковий керівник: к.т.н., м.н.с. асистент каф. “ММСА” Терентьєв О.М. Київ - 2010 Виконавець: студентка групи КА-46 Акулініна О.А.

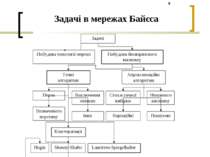
Постановка задачі дослідження Аналіз існуючих методів побудови ймовірнісного висновку в мережах Байєса. Розробка модифікації LS-методу побудови ймовірнісного висновку в мережі Байєса. Поетапний опис запропонованого алгоритму та покрокова його реалізація на прикладі. Моделювання різних ситуацій в запропонованій мережі та порівняння отриманих результатів з іншими програмними продуктами на базі мереж Байєса. Порівняння запропонованого модифікованого LS-методу та інших алгоритмів кластеризації.

Виникнення назви “Мережа Байєса” Термін “мережа Байєса” був запропонований у 1985 році Джуді Перлом (Judea Pearl). Назва мережі Байєса пов’язана з використанням правила Байєса у задачі побудови ймовірнісного висновку в мережі.

Поняття мережі Байєса Мережа Байєса представляє собою пару , де - це направлений ациклічний граф, а - множина таблиць умовних ймовірностей вершин. Сукупний ймовірнісний розподіл в МБ обчислюється за формулою:

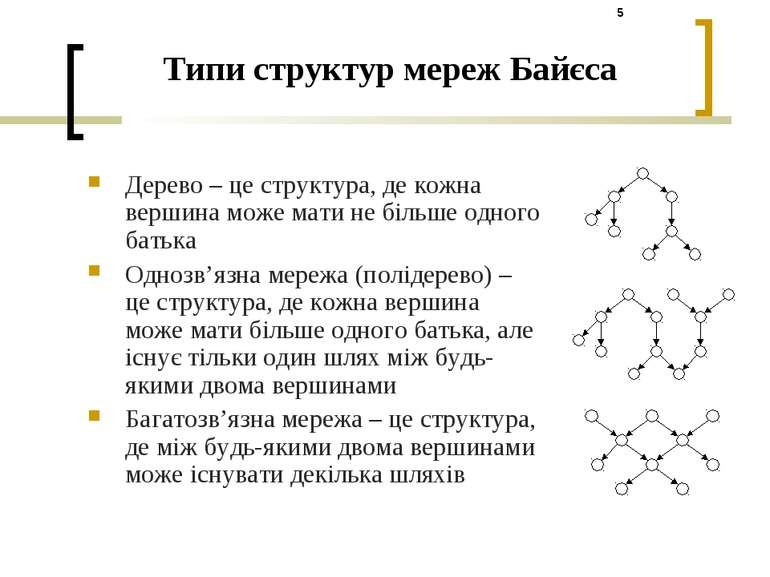
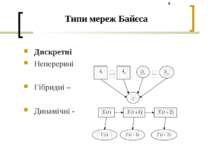
Типи структур мереж Байєса Дерево – це структура, де кожна вершина може мати не більше одного батька Однозв’язна мережа (полідерево) – це структура, де кожна вершина може мати більше одного батька, але існує тільки один шлях між будь-якими двома вершинами Багатозв’язна мережа – це структура, де між будь-якими двома вершинами може існувати декілька шляхів

Типи мереж Байєса Дискретні Неперервні Гібридні – Динамічні -

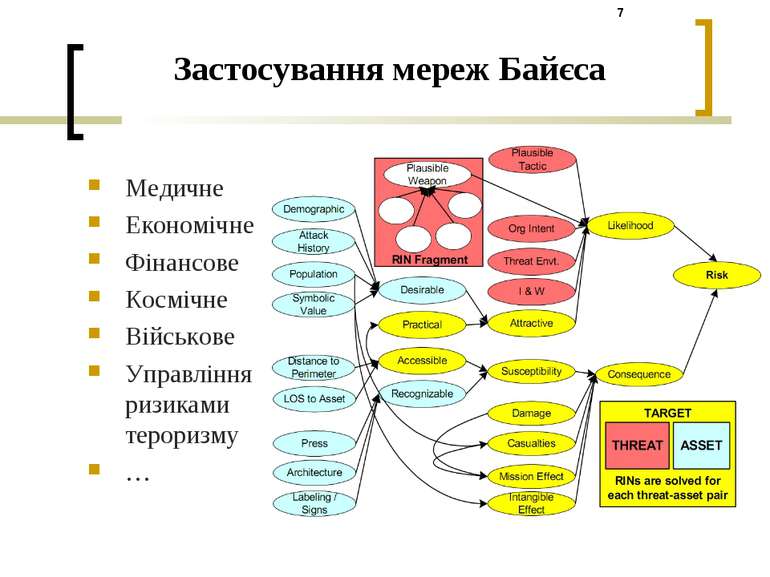
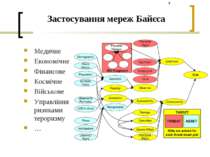
Застосування мереж Байєса Медичне Економічне Фінансове Космічне Військове Управління ризиками тероризму …

Задачі в мережах Байєса

Ймовірнісний висновок Метою ймовірнісного висновку є знаходження - апостеріорної ймовірності шуканих вершин , при деякому значенні спостережуваних вершин Задача побудови ймовірнісного висновку є складною з обчислювальної точки зору та неоднозначною

LS-метод : перший етап – побудова об’єднаного дерева Запропонували Lauritzen та Spiegelhalter у 1988 р. Етапи методу: I. Побудова об’єднаного дерева : Моралізація графу Приведення графу до ненаправленого Триангуляція графу Побудова дерева клік Побудова об’єднаного дерева Заповнення об’єднаного дерева таблицями

II. Алгоритм пропагації: Введення спостережень в таблиці Сходження догори Сходження донизу Розрахунок ймовірностей станів вершин Суть модифікації LS-методу полягає в новому принципі заповнюванні таблиць умовних ймовірностей, що описують кліки об’єднаного дерева LS-метод : другий етап – алгоритм пропагації

Модифікація LS-методу Заповнення починається з листів дерева і послідовно перебираються усі кліки. Розглядаються "невідмічені" вершини в необробленій кліці: Якщо серед "невідмічених" вершин є така, яка не зустрічається в інших необроблених кліках, то таблиця повинна мати вигляд - у такому разі ця вершина "відмічена" і кліка вважається обробленою. Якщо в первинній МБ такої таблиці немає або така вершина не одна, то використовується таблиця сукупного розподілу ймовірності - у такому разі усі вершини кліки "відмічені" і кліка оброблена.

Якщо в кліці є вже "відмічені" вершини і всього одна "невідмічена" вершина, то використовується таблиця виду з первинної МБ - у такому разі ця вершина "відмічена" і кліка вважається обробленою. Якщо в кліці є вже "відмічені" вершини, а "невідмічених" вершин декілька, то використовується таблиця сукупного розподілу ймовірності "невідмічених" вершин і тоді ці вершини "відмічені", а кліка вважається обробленою. Якщо в необробленій кліці усі вершини вже "відмічені", то кліка заповнюється таблицею виду і вважається обробленою. Модифікація LS-методу

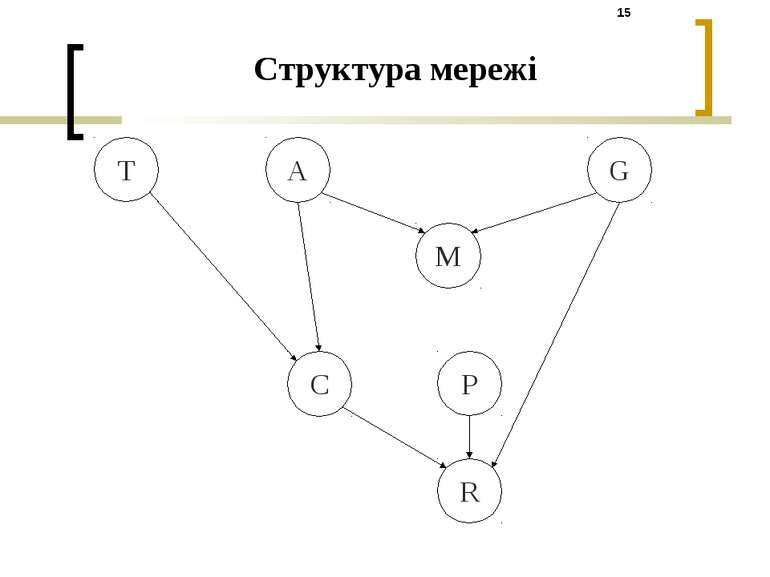
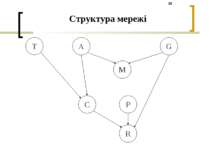
Приклад використання модифікованого LS-методу для визначення кредитоспроможності фізичних осіб Вхідні дані: База даних клієнтів банку з 3347 записів Топологія мережі побудована за допомогою евристичного методу побудови мереж Байєса за навчальними даними Вершини мережі: T – Type of Contract A – Age G – Gender M – Marital Status C – Total Credit Mount P – Contact Person R – Result (creditworthiness)

Структура мережі

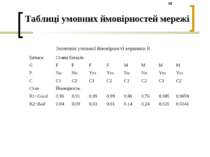
Таблиці умовних ймовірностей мережі Значення умовної ймовірності вершини T Значення умовної ймовірності вершини A Значення умовної ймовірності вершини C Стан Ймовірність T1 = Employ full time 0,875 T2 = Pensioner 0,061 T3 = Self Employer 0,064 Стан Ймовірність A1=More then 36 0,45 A2=Low then 36 0,55 Батьки Стани батьків T T1 T1 T2 T2 T3 T3 A A1 A2 A1 A2 A1 A2 Стан Ймовірність C1= Low then 2100 UAH 0,55 0,6 0,63 0,8 0,4 0,46 C2= More then 2100 UAH 0,45 0,4 0,37 0,2 0,6 0,54

Таблиці умовних ймовірностей мережі Значення умовної ймовірності вершини M Значення умовної ймовірності вершини G Значення умовної ймовірності вершини P Батьки Стани батьків A A1 A2 A1 A2 G F F M M Стан Ймовірність M1=Civil marriage 0,0361 0,0841 0,0321 0,0903 M2=Divorce 0,1996 0,0771 0,0681 0,0819 M3=Married 0,5848 0,5455 0,8517 0,1218 M4=Single 0,0792 0,2853 0,0341 0,706 M5=Widowed 0,1003 0,008 0,014 0 Стан Ймовірність F=Female 0,47 M=Male 0,53 Стан Ймовірність No 0,44 Yes 0,56

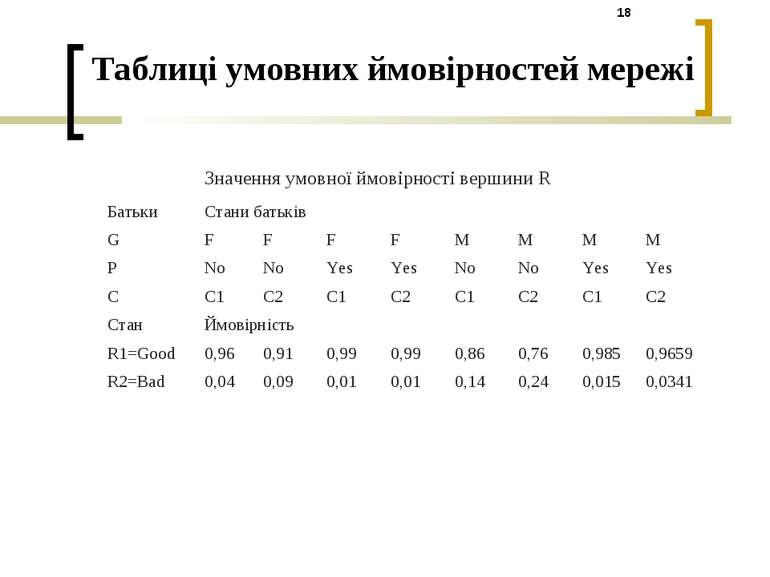
Таблиці умовних ймовірностей мережі Значення умовної ймовірності вершини R Батьки Стани батьків G F F F F M M M M P No No Yes Yes No No Yes Yes C C1 C2 C1 C2 C1 C2 C1 C2 Стан Ймовірність R1=Good 0,96 0,91 0,99 0,99 0,86 0,76 0,985 0,9659 R2=Bad 0,04 0,09 0,01 0,01 0,14 0,24 0,015 0,0341

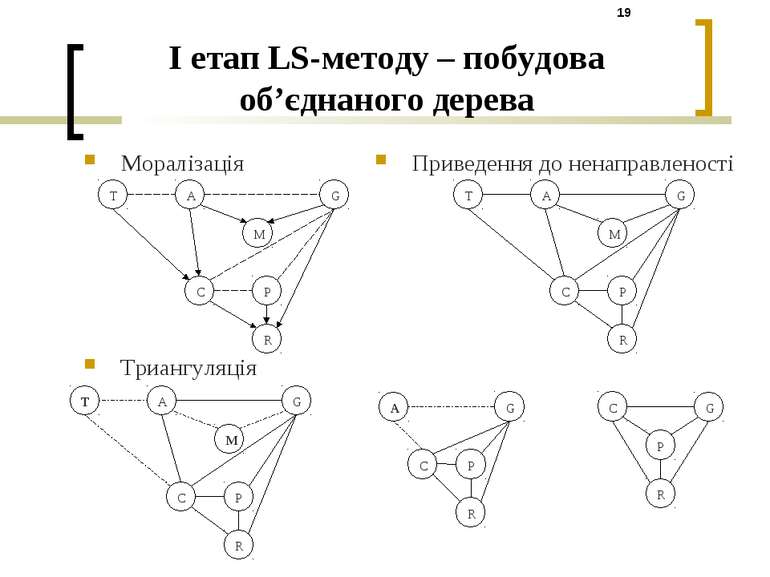
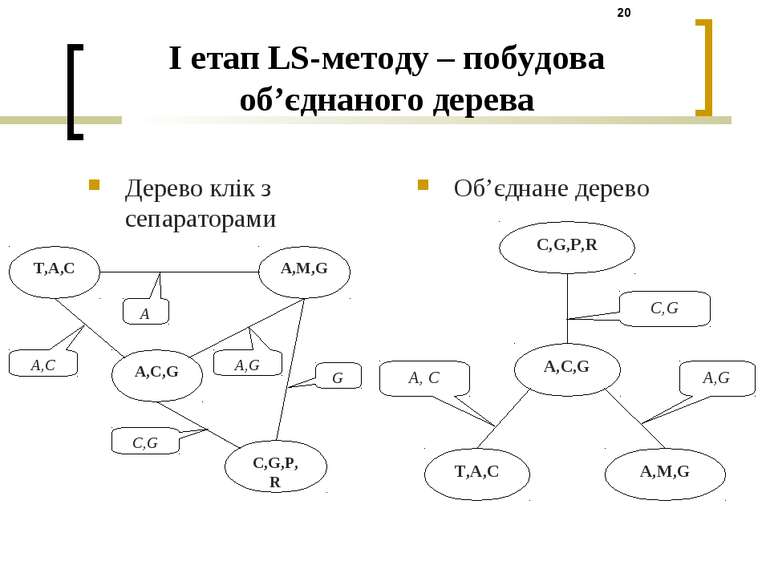
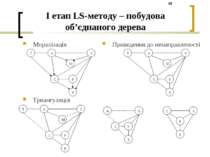
I етап LS-методу – побудова об’єднаного дерева Моралізація Триангуляція Приведення до ненаправленості

I етап LS-методу – побудова об’єднаного дерева Дерево клік з сепараторами Об’єднане дерево

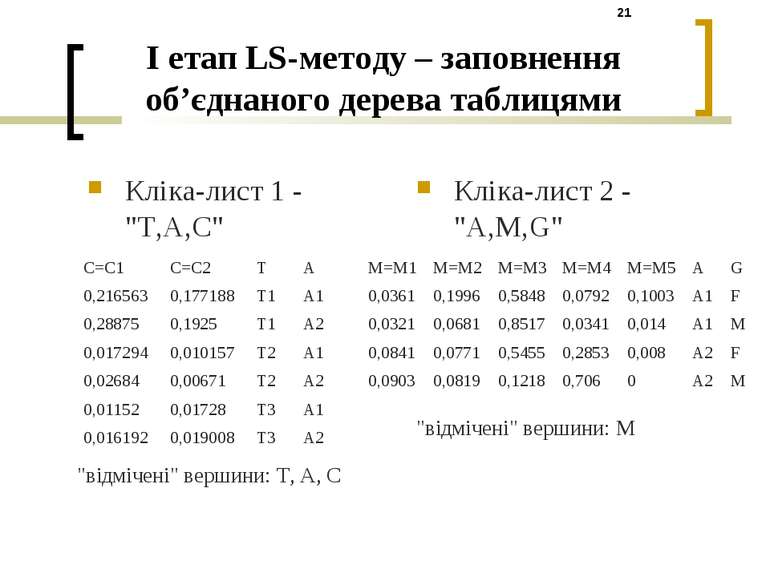
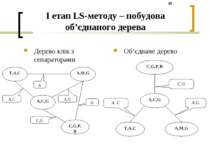
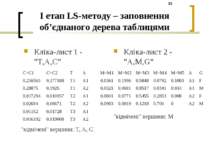
I етап LS-методу – заповнення об’єднаного дерева таблицями Кліка-лист 1 - "T,A,C" Кліка-лист 2 - "A,M,G" "відмічені" вершини: T, A, C "відмічені" вершини: M C=C1 C=C2 T A 0,216563 0,177188 T1 A1 0,28875 0,1925 T1 A2 0,017294 0,010157 T2 A1 0,02684 0,00671 T2 A2 0,01152 0,01728 T3 A1 0,016192 0,019008 T3 A2 M=M1 M=M2 M=M3 M=M4 M=M5 A G 0,0361 0,1996 0,5848 0,0792 0,1003 A1 F 0,0321 0,0681 0,8517 0,0341 0,014 A1 M 0,0841 0,0771 0,5455 0,2853 0,008 A2 F 0,0903 0,0819 0,1218 0,706 0 A2 M

I етап LS-методу – заповнення об’єднаного дерева таблицями Кліка 3 – "A,C,G" Корінь дерева – "R,C,P,G" "відмічені" вершини: G "відмічені" вершини: P,R C=C1 C=C2 A G 0,47 0,47 A1 F 0,53 0,53 A1 M 0,47 0,47 A2 F 0,53 0,53 A2 M R=R1 R=R2 C P G 0,114551 0,004772944 C1 No F 0,115719 0,018837896 C1 No M 0,150348 0,001518664 C1 Yes F 0,168685 0,002568804 C1 Yes M 0,079604 0,007872876 C2 No F 0,074969 0,023674464 C2 No M 0,11022 0,001113336 C2 Yes F 0,121265 0,004281132 C2 Yes M

II етап LS-методу – алгоритм пропагації заповнимо нулями входження P=Yes в корені заповнимо нулями входження G=F в кліці 3 - "A,C,G" Введення спостережень P=No (поручителя немає), G=M (стать - чоловіча) в таблиці R=R1 R=R2 C P G 0,114551 0,004772944 C1 No F 0,115719 0,018837896 C1 No M 0 0 C1 Yes F 0 0 C1 Yes M 0,079604 0,007872876 C2 No F 0,074969 0,023674464 C2 No M 0 0 C2 Yes F 0 0 C2 Yes M C=C1 C=C2 A G 0 0 A1 F 0,53 0,53 A1 M 0 0 A2 F 0,53 0,53 A2 M

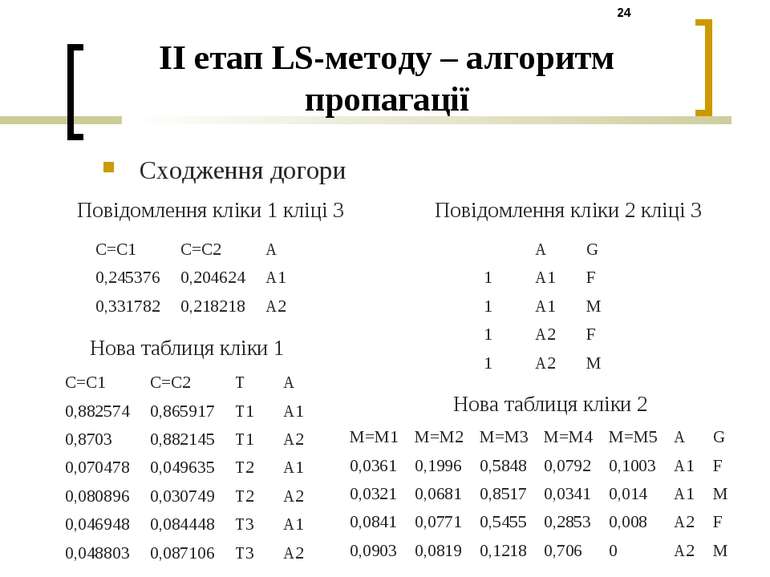
II етап LS-методу – алгоритм пропагації Сходження догори Повідомлення кліки 1 кліці 3 Нова таблиця кліки 1 Повідомлення кліки 2 кліці 3 Нова таблиця кліки 2 C=C1 C=C2 A 0,245376 0,204624 A1 0,331782 0,218218 A2 C=C1 C=C2 T A 0,882574 0,865917 T1 A1 0,8703 0,882145 T1 A2 0,070478 0,049635 T2 A1 0,080896 0,030749 T2 A2 0,046948 0,084448 T3 A1 0,048803 0,087106 T3 A2 A G 1 A1 F 1 A1 M 1 A2 F 1 A2 M M=M1 M=M2 M=M3 M=M4 M=M5 A G 0,0361 0,1996 0,5848 0,0792 0,1003 A1 F 0,0321 0,0681 0,8517 0,0341 0,014 A1 M 0,0841 0,0771 0,5455 0,2853 0,008 A2 F 0,0903 0,0819 0,1218 0,706 0 A2 M

Нова таблиця кліки 3 Повідомлення кліки 3 кореню Нова таблиця кліки 3 Нова таблиця кореня II етап LS-методу – алгоритм пропагації C=C1 C=C2 A G 0 0 A1 F 0,130049 0,10845072 A1 M 0 0 A2 F 0,175844 0,11565554 A2 M C=C1 C=C2 G 0 0 F 0,305894 0,22410626 M C=C1 C=C2 A G 0 0 A1 F 0,4251453 0,483925438 A1 M 0 0 A2 F 0,5748547 0,516074562 A2 M R=R1 R=R2 C P G 0 0 C1 No F 0,035398 0,005762394 C1 No M 0 0 C1 Yes F 0 0 C1 Yes M 0 0 C2 No F 0,016801 0,005305596 C2 No M 0 0 C2 Yes F 0 0 C2 Yes M

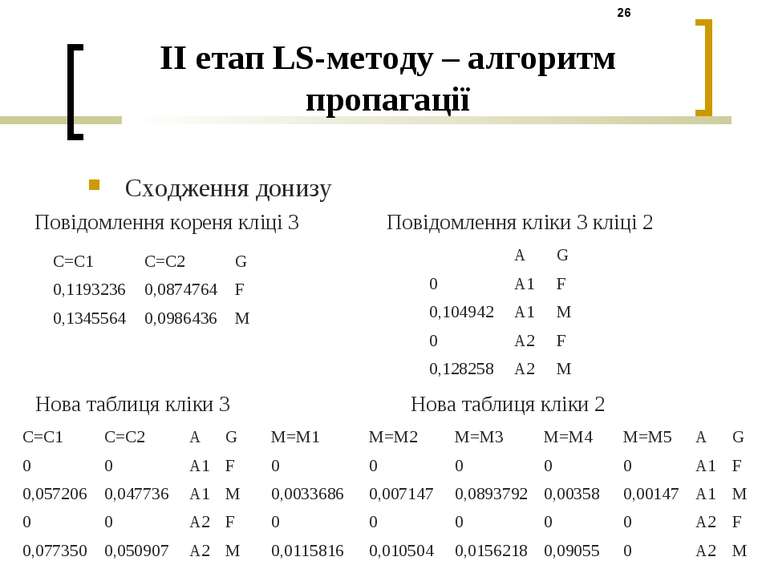
II етап LS-методу – алгоритм пропагації Сходження донизу Повідомлення кореня кліці 3 Нова таблиця кліки 3 Повідомлення кліки 3 кліці 2 Нова таблиця кліки 2 C=C1 C=C2 G 0,1193236 0,0874764 F 0,1345564 0,0986436 M C=C1 C=C2 A G 0 0 A1 F 0,057206 0,047736 A1 M 0 0 A2 F 0,077350 0,050907 A2 M A G 0 A1 F 0,104942 A1 M 0 A2 F 0,128258 A2 M M=M1 M=M2 M=M3 M=M4 M=M5 A G 0 0 0 0 0 A1 F 0,0033686 0,007147 0,0893792 0,00358 0,00147 A1 M 0 0 0 0 0 A2 F 0,0115816 0,010504 0,0156218 0,09055 0 A2 M

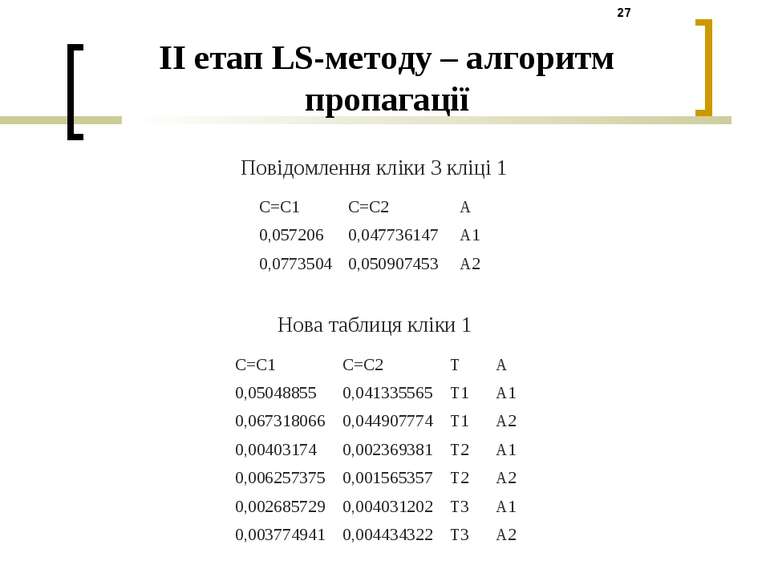
Повідомлення кліки 3 кліці 1 Нова таблиця кліки 1 II етап LS-методу – алгоритм пропагації C=C1 C=C2 A 0,057206 0,047736147 A1 0,0773504 0,050907453 A2 C=C1 C=C2 T A 0,05048855 0,041335565 T1 A1 0,067318066 0,044907774 T1 A2 0,00403174 0,002369381 T2 A1 0,006257375 0,001565357 T2 A2 0,002685729 0,004031202 T3 A1 0,003774941 0,004434322 T3 A2

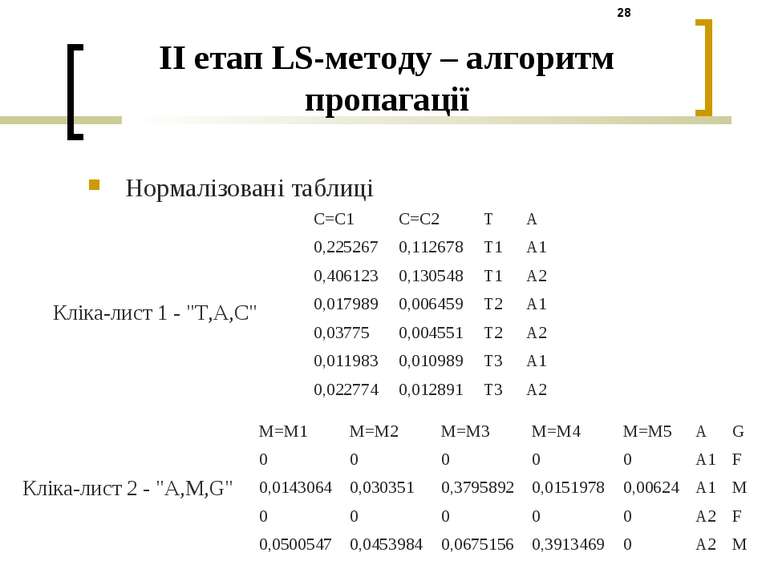
II етап LS-методу – алгоритм пропагації Нормалізовані таблиці Кліка-лист 1 - "T,A,C" Кліка-лист 2 - "A,M,G" C=C1 C=C2 T A 0,225267 0,112678 T1 A1 0,406123 0,130548 T1 A2 0,017989 0,006459 T2 A1 0,03775 0,004551 T2 A2 0,011983 0,010989 T3 A1 0,022774 0,012891 T3 A2 M=M1 M=M2 M=M3 M=M4 M=M5 A G 0 0 0 0 0 A1 F 0,0143064 0,030351 0,3795892 0,0151978 0,00624 A1 M 0 0 0 0 0 A2 F 0,0500547 0,0453984 0,0675156 0,3913469 0 A2 M

II етап LS-методу – алгоритм пропагації Кліка 3 - "A,C,G" Корінь дерева - " R,C,P,G" C=C1 C=C2 A G 0 0 A1 F 0,276591 0,169093 A1 M 0 0 A2 F 0,373989 0,180327 A2 M R=R1 R=R2 C P G 0 0 C1 No F 0,559498 0,091081 C1 No M 0 0 C1 Yes F 0 0 C1 Yes M 0 0 C2 No F 0,26556 0,083861 C2 No M 0 0 C2 Yes F 0 0 C2 Yes M

Розрахунок ймовірностей станів вершин Для вершини T підсумовуються її значення в кліці 1 Для вершини A підсумовуються її значення в кліці 3: Для вершини C підсумовуються її значення в кліці 3: II етап LS-методу – алгоритм пропагації

Для вершини M підсумовуються її значення в кліці 2: Для вершини R підсумовуються її значення в корені: II етап LS-методу – алгоритм пропагації

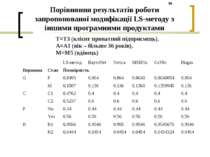
Порівняння результатів роботи запропонованої модифікації LS-методу з іншими програмними продуктами Програма Метод ймовірнісного висновку BayesNet Метод ймовірнісного висновку в байєсовских мережах за навчальними даними Netica Метод виключення об’єднаних дерев Hugin - Expert Метод Hugin MSBNx Метод заснований на поширенні повідомлень по дереву клік GeNIe Метод кластеризації

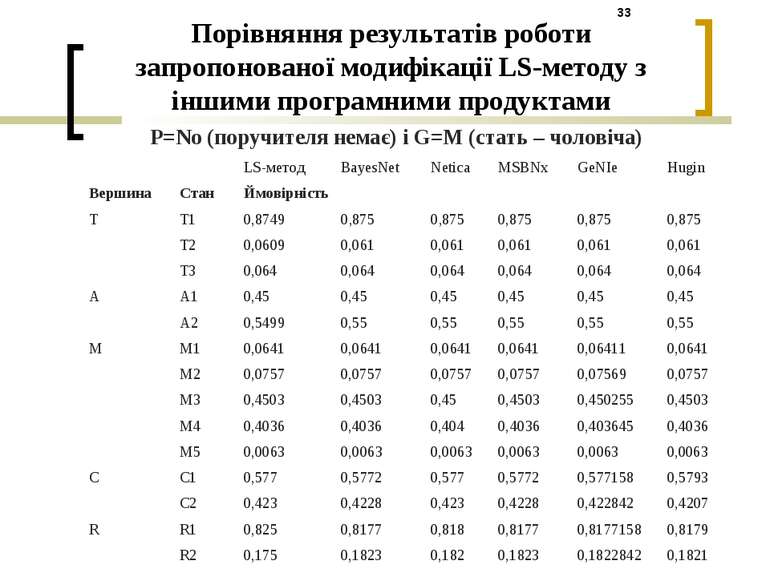
Порівняння результатів роботи запропонованої модифікації LS-методу з іншими програмними продуктами P=No (поручителя немає) і G=M (стать – чоловіча) LS-метод BayesNet Netica MSBNx GeNIe Hugin Вершина Стан Ймовірність T T1 0,8749 0,875 0,875 0,875 0,875 0,875 T2 0,0609 0,061 0,061 0,061 0,061 0,061 T3 0,064 0,064 0,064 0,064 0,064 0,064 A A1 0,45 0,45 0,45 0,45 0,45 0,45 A2 0,5499 0,55 0,55 0,55 0,55 0,55 M M1 0,0641 0,0641 0,0641 0,0641 0,06411 0,0641 M2 0,0757 0,0757 0,0757 0,0757 0,07569 0,0757 M3 0,4503 0,4503 0,45 0,4503 0,450255 0,4503 M4 0,4036 0,4036 0,404 0,4036 0,403645 0,4036 M5 0,0063 0,0063 0,0063 0,0063 0,0063 0,0063 C C1 0,577 0,5772 0,577 0,5772 0,577158 0,5793 C2 0,423 0,4228 0,423 0,4228 0,422842 0,4207 R R1 0,825 0,8177 0,818 0,8177 0,8177158 0,8179 R2 0,175 0,1823 0,182 0,1823 0,1822842 0,1821

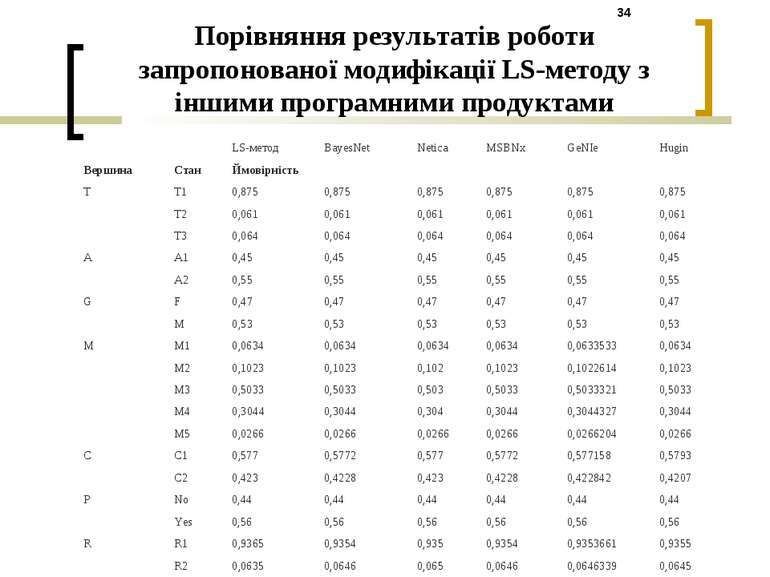
Порівняння результатів роботи запропонованої модифікації LS-методу з іншими програмними продуктами LS-метод BayesNet Netica MSBNx GeNIe Hugin Вершина Стан Ймовірність T T1 0,875 0,875 0,875 0,875 0,875 0,875 T2 0,061 0,061 0,061 0,061 0,061 0,061 T3 0,064 0,064 0,064 0,064 0,064 0,064 A A1 0,45 0,45 0,45 0,45 0,45 0,45 A2 0,55 0,55 0,55 0,55 0,55 0,55 G F 0,47 0,47 0,47 0,47 0,47 0,47 M 0,53 0,53 0,53 0,53 0,53 0,53 M M1 0,0634 0,0634 0,0634 0,0634 0,0633533 0,0634 M2 0,1023 0,1023 0,102 0,1023 0,1022614 0,1023 M3 0,5033 0,5033 0,503 0,5033 0,5033321 0,5033 M4 0,3044 0,3044 0,304 0,3044 0,3044327 0,3044 M5 0,0266 0,0266 0,0266 0,0266 0,0266204 0,0266 C C1 0,577 0,5772 0,577 0,5772 0,577158 0,5793 C2 0,423 0,4228 0,423 0,4228 0,422842 0,4207 P No 0,44 0,44 0,44 0,44 0,44 0,44 Yes 0,56 0,56 0,56 0,56 0,56 0,56 R R1 0,9365 0,9354 0,935 0,9354 0,9353661 0,9355 R2 0,0635 0,0646 0,065 0,0646 0,0646339 0,0645

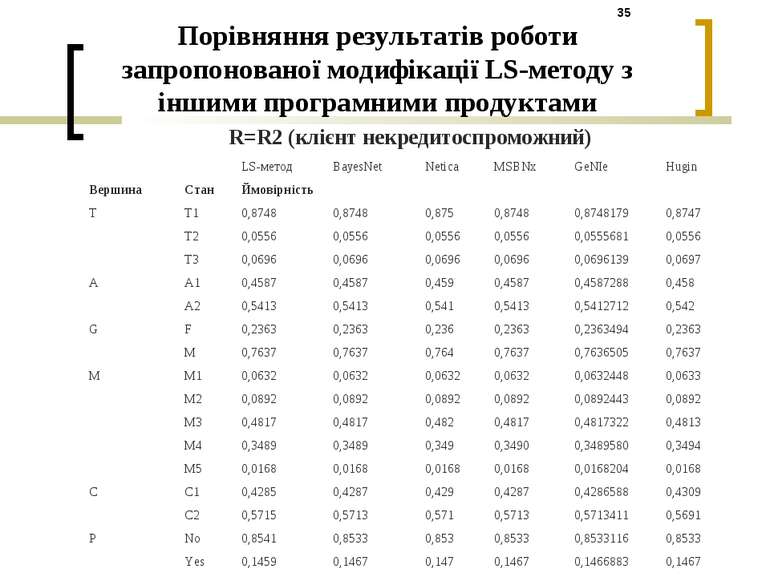
Порівняння результатів роботи запропонованої модифікації LS-методу з іншими програмними продуктами R=R2 (клієнт некредитоспроможний) LS-метод BayesNet Netica MSBNx GeNIe Hugin Вершина Стан Ймовірність T T1 0,8748 0,8748 0,875 0,8748 0,8748179 0,8747 T2 0,0556 0,0556 0,0556 0,0556 0,0555681 0,0556 T3 0,0696 0,0696 0,0696 0,0696 0,0696139 0,0697 A A1 0,4587 0,4587 0,459 0,4587 0,4587288 0,458 A2 0,5413 0,5413 0,541 0,5413 0,5412712 0,542 G F 0,2363 0,2363 0,236 0,2363 0,2363494 0,2363 M 0,7637 0,7637 0,764 0,7637 0,7636505 0,7637 M M1 0,0632 0,0632 0,0632 0,0632 0,0632448 0,0633 M2 0,0892 0,0892 0,0892 0,0892 0,0892443 0,0892 M3 0,4817 0,4817 0,482 0,4817 0,4817322 0,4813 M4 0,3489 0,3489 0,349 0,3490 0,3489580 0,3494 M5 0,0168 0,0168 0,0168 0,0168 0,0168204 0,0168 C C1 0,4285 0,4287 0,429 0,4287 0,4286588 0,4309 C2 0,5715 0,5713 0,571 0,5713 0,5713411 0,5691 P No 0,8541 0,8533 0,853 0,8533 0,8533116 0,8533 Yes 0,1459 0,1467 0,147 0,1467 0,1466883 0,1467

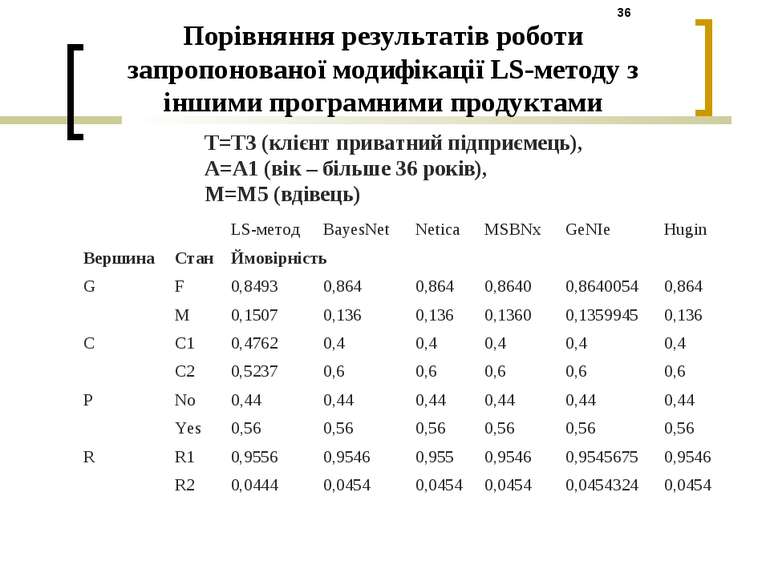
Порівняння результатів роботи запропонованої модифікації LS-методу з іншими програмними продуктами T=T3 (клієнт приватний підприємець), A=A1 (вік – більше 36 років), M=M5 (вдівець) LS-метод BayesNet Netica MSBNx GeNIe Hugin Вершина Стан Ймовірність G F 0,8493 0,864 0,864 0,8640 0,8640054 0,864 M 0,1507 0,136 0,136 0,1360 0,1359945 0,136 C C1 0,4762 0,4 0,4 0,4 0,4 0,4 C2 0,5237 0,6 0,6 0,6 0,6 0,6 P No 0,44 0,44 0,44 0,44 0,44 0,44 Yes 0,56 0,56 0,56 0,56 0,56 0,56 R R1 0,9556 0,9546 0,955 0,9546 0,9545675 0,9546 R2 0,0444 0,0454 0,0454 0,0454 0,0454324 0,0454

Порівняння результатів роботи запропонованої модифікації LS-методу з іншими програмними продуктами T=T3 (клієнт приватний підприємець), A=A2 (вік – менше 36 років), M=M4 (неодружений), C=C2 (сума кредиту - більше 2100 грн) LS-метод BayesNet Netica MSBNx GeNIe Hugin Вершина Стан Ймовірність G F 0,2411 0,2638 0,264 0,2638 0,264 0,2638 M 0,7589 0,7362 0,736 0,7362 0,736 0,7362 P No 0,44 0,44 0,44 0,44 0,44 0,44 Yes 0,56 0,56 0,56 0,56 0,56 0,56 R R1 0,8945 0,8963 0,896 0,8963 0,896 0,8963 R2 0,1055 0,1037 0,104 0,1037 0,104 0,1037

Порівняння алгоритмів кластеризації побудови ймовірнісного висновку Графічні структури для розповсюдження повідомлення LS - об’єднані дерева Hugin – об’єднані дерева з сепараторами SS – двійкові зв’язні дерева Обчислення ймовірностей окремих змінних LS – в кліках Hugin – в кліках та сепараторах SS – в вершинах

Обчислювальна ефективність Hugin виконує менше операцій ділень і додавань ніж LS SS не використовує операцій ділення Ефективність використання об’єму пам’яті LS потребує меншого об’єму пам’яті ніж Hugin в SS двійкове зв’язне дерево має більше вершин, ніж відповідне об’єднане дерево, але не кожна вершина в ньому потребує виділення пам’яті Порівняння алгоритмів кластеризації побудови ймовірнісного висновку

Порівняння алгоритмів кластеризації побудови ймовірнісного висновку на прикладі - максимальна кількість станів вершини - максимальне число вершин в кліці мінус 1 - кількість клік - кількість сусідів - ї кліки Метод Складність Пам’ять (fpn) Кількість операцій Час (мс) LS 135 108 35 Hugin 147 80 26 SS 283 120 39

Висновки Виконано аналіз існуючих методів побудови ймовірнісного висновку в мережах Байєса. Розроблена модифікація LS-методу побудови ймовірнісного висновку в мережі Байєса. Запропонований поетапний опис модифікованого алгоритму та покрокова його реалізація на прикладі. Виконане моделювання різних ситуацій в запропонованій мережі та порівняння отриманих результатів з іншими програмними продуктами на базі мереж Байєса. Виконане порівняння запропонованого модифікованого LS-методу та інших алгоритмів кластеризації.

Рекомендації щодо подальших досліджень Розробка оригінальної архітектури та реалізація комп’ютерної системи підтримки прийняття рішень для інтелектуального аналізу даних на основі мереж Байєса з використанням запропонованого методу для задачі побудови ймовірнісного висновку. Розширення запропонованого модифікованого LS-методу для використання в неперервних та гібридних мережах Байєса. Розробка нових методів побудови ймовірнісного висновку з меншою обчислювальною складністю на основі теорій Демпстера-Шефера і стохастичного моделювання методом Монте-Карло.

Акт впровадження Результати дисертаційної роботи були впроваджені на підприємстві “Номінал Інжинірінг” (“Crane Cash Code”)

Публікації : статті Подана для опублікування стаття в журнал “Wireless Sensor Network” M. Z. Zgurovskii, O.M. Terentyev, O.A. Akulinina, N.S. Guz. Methods of constructing probability inference in Bayesian networks using LS approach. Дата опублікування осінь-зима 2010 року. Подана до опублікування стаття в журнал "Вісник Університету «Україна»" Бідюк П.І., Акулініна О.А., Гуз Н.С., Свердел К.О. Побудова ймовірнісного висновку в мережах Байєса на основі LS-методу. Дата опублікування літо 2010 року.

Участь у ХІ Міжнародній науково-технічній конференції “Системний аналіз та інформаційні технології ” - 2009 рік Участь у ХІI Міжнародній науково-технічній конференції “Системний аналіз та інформаційні технології ” - 2010 рік Участь у Х Міжнародній науковій конференції “Інтелектуальні системи прийняття рішень і проблеми обчислювального інтелекту” – 2010 рік Публікації : конференції

Дякую за увагу!