Презентація на тему:
Представлення кореневих дерев. Двійкові дерева пошуку інформації

Алгоритми та структури даних Лекція 4 Представлення кореневих дерев. Двійкові дерева пошуку доц. Лавренюк А.М.

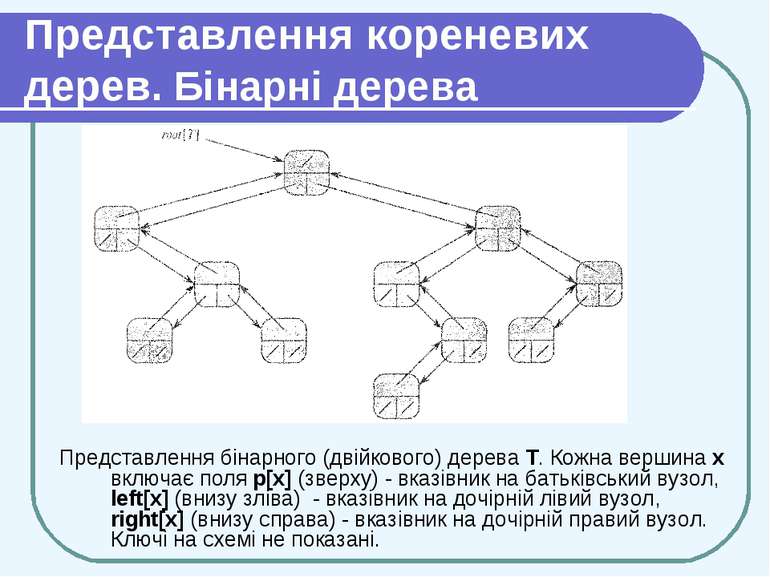
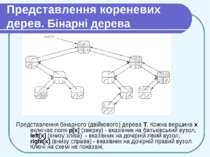
Представлення кореневих дерев. Бінарні дерева Представлення бінарного (двійкового) дерева Т. Кожна вершина х включає поля р[х] (зверху) - вказівник на батьківський вузол, left[x] (внизу зліва) - вказівник на дочірній лівий вузол, right[x] (внизу справа) - вказівник на дочірній правий вузол. Ключі на схемі не показані.

Представлення кореневих дерев. Бінарні дерева Якщо р [х] = nil, то х — корінь дерева. Якщо у вузла х немає дочірніх вузлів, то left [х] = right [х] = nil. Атрибут root [T] вказує на кореневий вузол дерева T. Якщо root [T] = NIL, то дерево Т пусте.

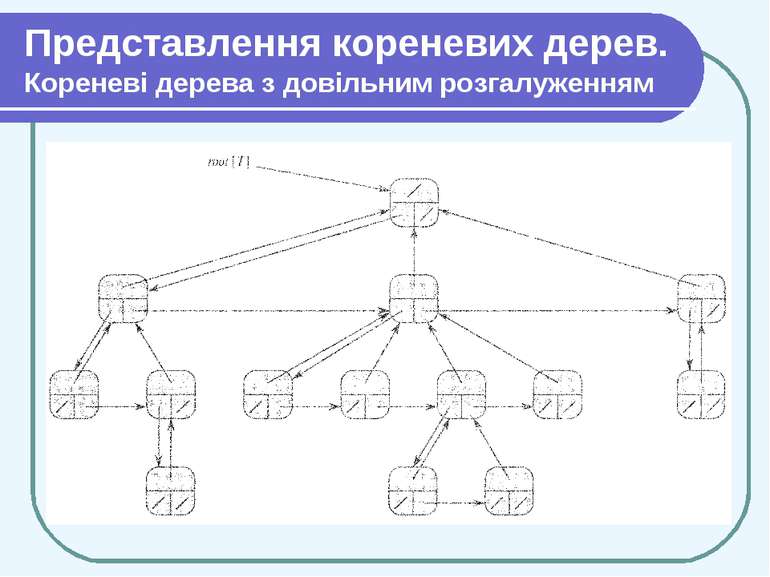
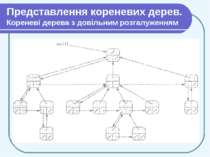
Представлення кореневих дерев. Кореневі дерева з довільним розгалуженням Схему представлення бінарних дерев можна узагальнити для дерев будь-якого класу, в яких кількість дочірніх вузлів не перевищує деякої константи k. При цьому поля правий і лівий замінюється полями child1, child2 ..., childk. Якщо кількість дочірніх елементів вузла не обмежена, то ця схема не працює, оскільки заздалегідь не відомо, місце для якої кількості полів потрібно виділити. Крім того, якщо кількість дочірніх елементів k обмежено великою константою, але насправді у багатьох вузлів нащадків набагато менше, то значний об'єм пам'яті витрачається марно.

Представлення кореневих дерев. Кореневі дерева з довільним розгалуженням Будь-яке дерево можна перетворити в двійкове. При цьому в кожної вершини буде не більше двох дітей: ліве дитя залишиться тим же, а правим дитям стане вершина, яка була правим сусідом (безпосередньо наступним дитям того ж батька). Схема зберігання дерев з довільним розгалуженням, основана на цій ідеї, називається «Ліве дитя — правий сусід» (left-child, right-sibling representation) або представлення з лівим дочірнім і правим сестринським вузлами.

Представлення кореневих дерев. Кореневі дерева з довільним розгалуженням Як і раніше в кожній вершині зберігається вказівник р на батька і атрибут root[T] є вказівником на корінь дерева. Окрім р, в кожній вершині зберігаються ще два вказівники: 1. left-child[x] вказує на найлівіше дитя вершини х; 2. right-sibling[x] вказує на найближчого справа сусіда вершини х («наступного за старшинством брата»)

Представлення кореневих дерев. Кореневі дерева з довільним розгалуженням

Представлення кореневих дерев. Кореневі дерева з довільним розгалуженням Якщо вузол х не має нащадків, то left - child [x] = NIL , а якщо вузол х - крайній правий дочірній елемент якогось батьківського елементу, то right - sibling [x] = NIL.

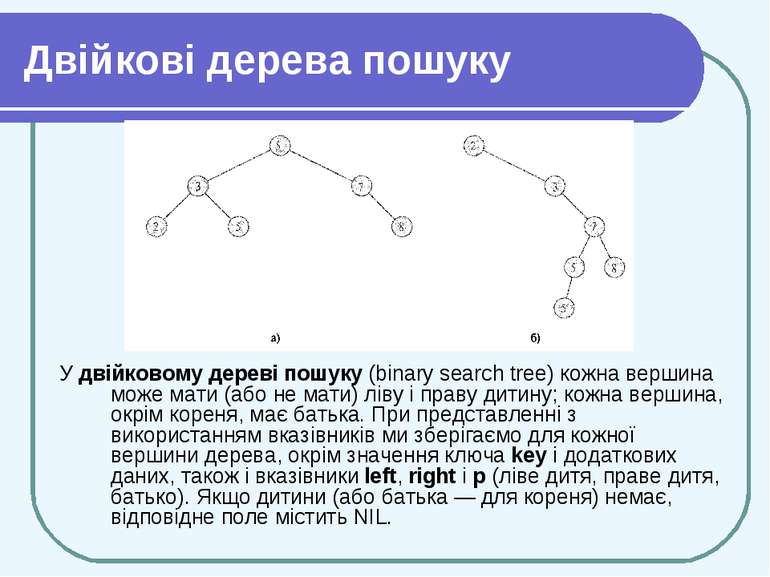
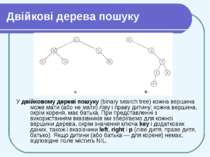
Двійкові дерева пошуку У двійковому дереві пошуку (binary search tree) кожна вершина може мати (або не мати) ліву і праву дитину; кожна вершина, окрім кореня, має батька. При представленні з використанням вказівників ми зберігаємо для кожної вершини дерева, окрім значення ключа key і додаткових даних, також і вказівники left, right і р (ліве дитя, праве дитя, батько). Якщо дитини (або батька — для кореня) немає, відповідне поле містить NIL.

Двійкові дерева пошуку Ключі в двійковому дереві пошуку зберігаються з дотриманням властивості впорядкованості (binary-search-tree property): Нехай х - довільна вершина двійкового дерева пошуку. Якщо вершина y знаходиться в лівому піддереві вершини х, то key[y] = кеу[х].

Двійкові дерева пошуку Властивість впорядкованості дозволяє надрукувати всі ключі в неспадаючому порядку за допомогою простого рекурсивного алгоритму (inorder tree walk). Цей алгоритм друкує ключ кореня піддерева після всіх ключів його лівого піддерева, але перед ключами правого піддерева (центрований (симетричний) обхід дерева). Порядок, при якому корінь передує обом піддеревам, називається preorder (обхід в прямому порядку); порядок, в якому корінь слідує за ними, називається postorder (обхід в зворотному порядку).

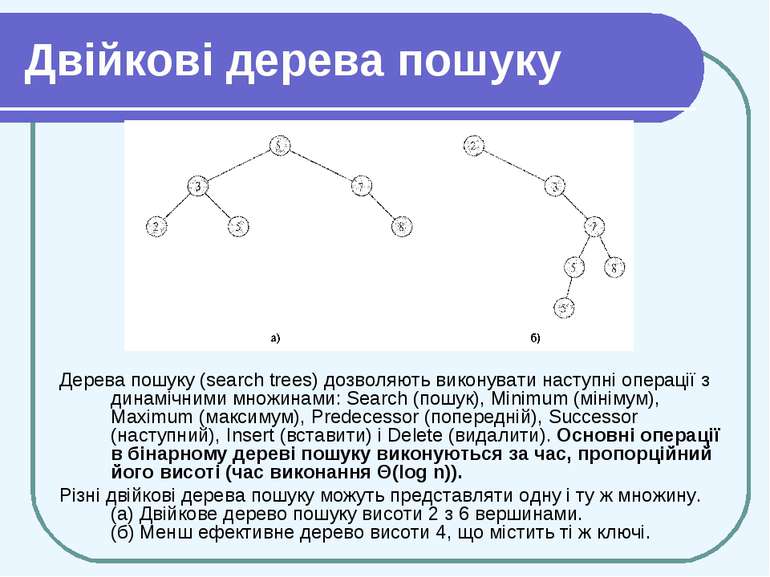
Двійкові дерева пошуку Дерева пошуку (search trees) дозволяють виконувати наступні операції з динамічними множинами: Search (пошук), Minimum (мінімум), Maximum (максимум), Predecessor (попередній), Successor (наступний), Insert (вставити) і Delete (видалити). Основні операції в бінарному дереві пошуку виконуються за час, пропорційний його висоті (час виконання Θ(log n)). Різні двійкові дерева пошуку можуть представляти одну і ту ж множину. (а) Двійкове дерево пошуку висоти 2 з 6 вершинами. (б) Менш ефективне дерево висоти 4, що містить ті ж ключі.

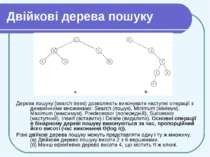
Двійкові дерева пошуку Виклик Inorder-Tree-Walk (root[Т]) друкує (використовуючи центрований обхід) всі ключі, що входять в дерево T з коренем root[T].

Двійкові дерева пошуку Наприклад, для обох дерев мал. (а) і (б) буде надруковано 2,3,5,5,7,8. Час роботи цієї процедури на дереві з n вершинами є Θ(n): на кожну вершину витрачається обмежений час (окрім рекурсивних викликів) і кожна вершина обробляється один раз.

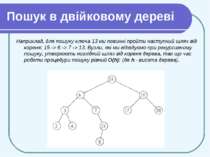
Пошук в двійковому дереві Найбільш поширеною операцією, що виконується з бінарним деревом пошуку, є пошук в ньому певного ключа. Розглянемо операції пошуку, знаходження мінімального та максимального, попереднього та наступного елементу і покажемо, що всі вони можуть бути виконані в бінарному дереві пошуку висотою h за час О(h).

Пошук в двійковому дереві Процедура пошуку отримує на вхід шуканий ключ k і вказівник х на корінь піддерева, в якому проводиться пошук. Вона повертає вказівник на вершину з ключем k (якщо така є) або спеціальне значення NIL (NULL) (якщо такої вершини немає).

Пошук в двійковому дереві В процесі пошуку ми рухаємося від кореня, порівнюючи ключ k з ключем, що зберігається в поточній вершині х. Якщо вони рівні, пошук завершується. Якщо kкеу[х], то пошук продовжується в правому піддереві.

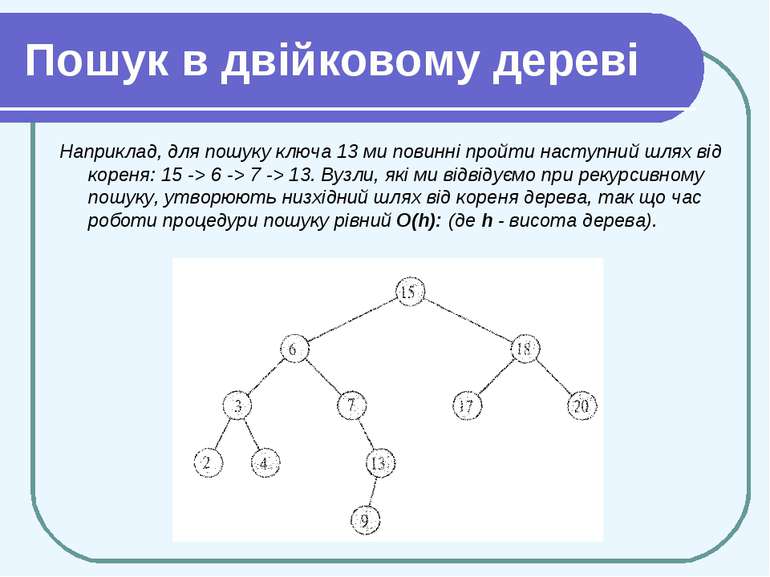
Пошук в двійковому дереві Наприклад, для пошуку ключа 13 ми повинні пройти наступний шлях від кореня: 15 -> 6 -> 7 -> 13. Вузли, які ми відвідуємо при рекурсивному пошуку, утворюють низхідний шлях від кореня дерева, так що час роботи процедури пошуку рівний O(h): (де h - висота дерева).

Пошук в двійковому дереві Ось ітераційна версія тієї ж процедури (яка, як правило, ефективніша):

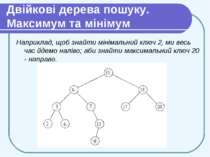
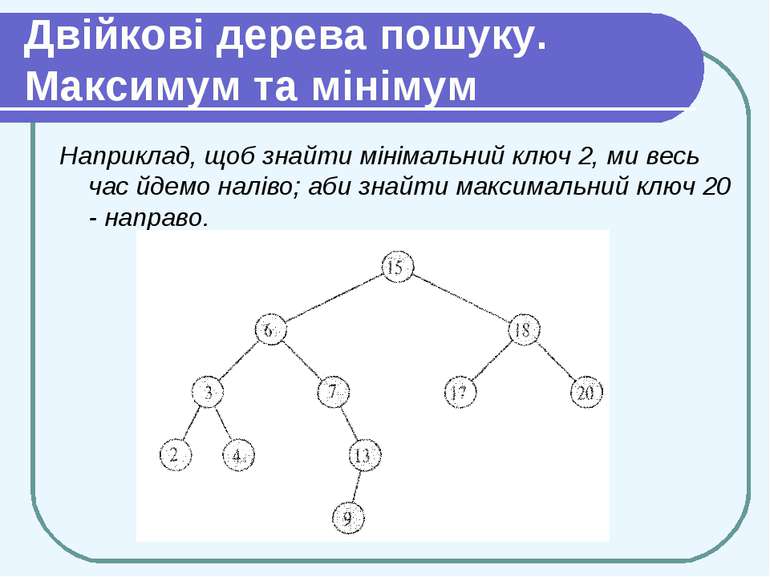
Двійкові дерева пошуку. Максимум та мінімум Мінімальний ключ в дереві пошуку можна знайти, пройшовши за вказівниками left від кореня (поки не впремося в nil). Процедура повертає вказівник на мінімальний елемент піддерева з коренем х . Властивість впорядкованості гарантує правильність процедури Tree-Minimum. Якщо у вершини x немає лівої дитини, то мінімальний елемент піддерева з коренем x є x, оскільки будь-який ключ в правому піддереві не менший кеу[х]. Якщо ж ліве піддерево вершини x не порожнє, то мінімальний елемент піддерева з коренем x знаходиться в цьому лівому піддереві (оскільки сам x і всі елементи правого піддерева більші).

Двійкові дерева пошуку. Максимум та мінімум Алгоритм Tree-Maximum симетричний. Обидва алгоритми вимагають часу O(h), де h - висота дерева (оскільки рухаються по дереву лише вниз).

Двійкові дерева пошуку. Максимум та мінімум Наприклад, щоб знайти мінімальний ключ 2, ми весь час йдемо наліво; аби знайти максимальний ключ 20 - направо.

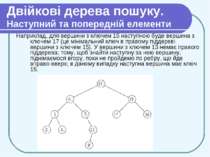
Двійкові дерева пошуку. Наступний та попередній елементи Інколи, маючи вузол в бінарному дереві пошуку, потрібно визначити, який вузол слідує за ним у відсортованій послідовності, що визначається порядком центрованого обходу бінарного дерева, і який вузол передує даному. Якщо всі ключі різні, наступний по відношенню до вузла х є вузол з найменшим ключем, більшим за key [x]. Структура бінарного дерева пошуку дозволяє нам знайти цей вузол навіть не виконуючи порівняння ключів. Приведена далі процедура повертає вузол, наступний за вузлом х в бінарному дереві пошуку (якщо такий існує) і NIL, якщо х має найбільший ключ в бінарному дереві (останній в дереві).

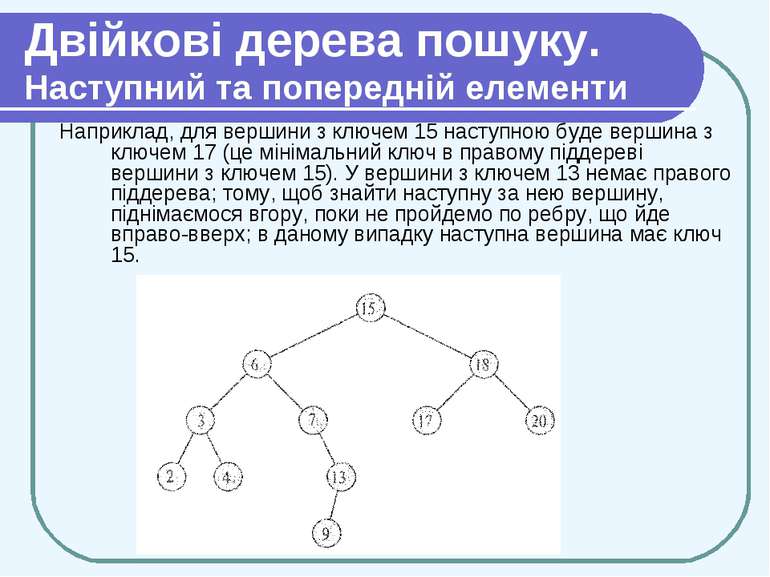
Двійкові дерева пошуку. Наступний та попередній елементи Процедура Tree-successor окремо розглядає два випадки. Якщо праве піддерево вершини х не порожнє, то наступний за х елемент — це мінімальний елемент в цьому піддереві і рівний Tree-Minimum(right[x]). Нехай тепер праве піддерево вершини х порожнє. Тоді ми йдемо від х вгору, поки не знайдемо вершину, що є лівим сином свого батька (рядки 3-7). Цей батько (якщо він є) і буде шуканим елементом.

Двійкові дерева пошуку. Наступний та попередній елементи Наприклад, для вершини з ключем 15 наступною буде вершина з ключем 17 (це мінімальний ключ в правому піддереві вершини з ключем 15). У вершини з ключем 13 немає правого піддерева; тому, щоб знайти наступну за нею вершину, піднімаємося вгору, поки не пройдемо по ребру, що йде вправо-вверх; в даному випадку наступна вершина має ключ 15.

Двійкові дерева пошуку. Наступний та попередній елементи Час роботи процедури Tree-Successor на дереві висоти h є O(h), оскільки ми рухаємося або лише вгору, або лише вниз. Процедура Tree-Predecessor симетрична. Таким чином, операції Search, Minimum, Maximum, Successor і Predecessor на дереві висоти h виконуються за час О(h).

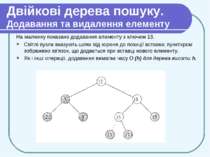
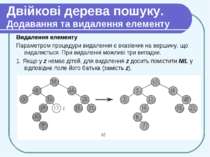
Двійкові дерева пошуку. Додавання та видалення елементу Ці операції змінюють дерево, зберігаючи властивість впорядкованості. Додавання елементу Процедура Tree-Insert додає заданий елемент у відповідне місце дерева T (зберігаючи властивість впорядкованості). Параметром процедури є вказівник z на нову вершину, в яку поміщені значення key[z] (значення ключа, що додається), left[z]= NIL і right[z]= NIL. В ході роботи процедура змінює дерево T і (можливо) деякі поля вершини z, після чого нова вершина з даним значенням ключа виявляється вставленою у відповідне місце дерева.

Двійкові дерева пошуку. Додавання та видалення елементу Рухаємося вниз по дереву, почавши з його кореня. При цьому у вершині y зберігається вказівник на батька вершини х (цикл в ряд. 3-7). Порівнюючи key[z] з кеу[х], процедура вирішує, куди йти — наліво чи направо. Процес завершується, коли х стає рівним NIL. NIL стоїть якраз там, куди треба помістити z, що і робиться у ряд. 8-13.

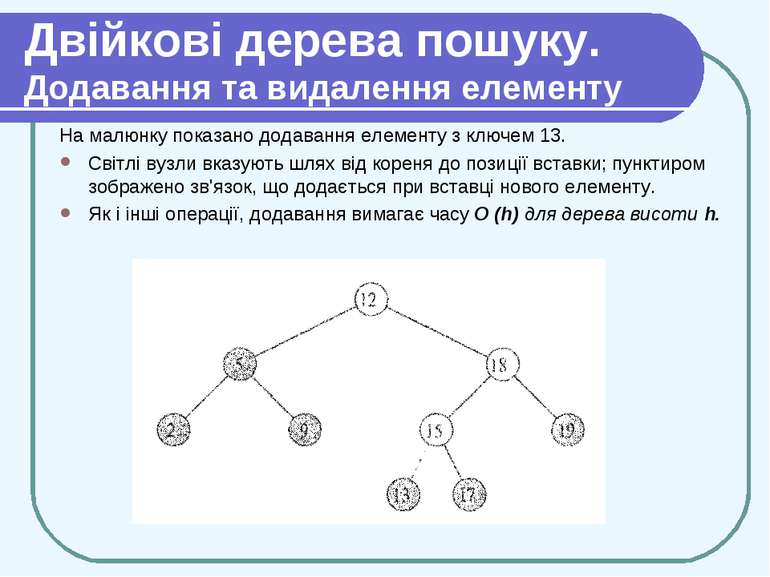
Двійкові дерева пошуку. Додавання та видалення елементу На малюнку показано додавання елементу з ключем 13. Світлі вузли вказують шлях від кореня до позиції вставки; пунктиром зображено зв'язок, що додається при вставці нового елементу. Як і інші операції, додавання вимагає часу O (h) для дерева висоти h.

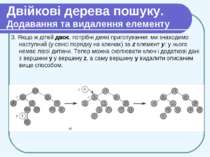
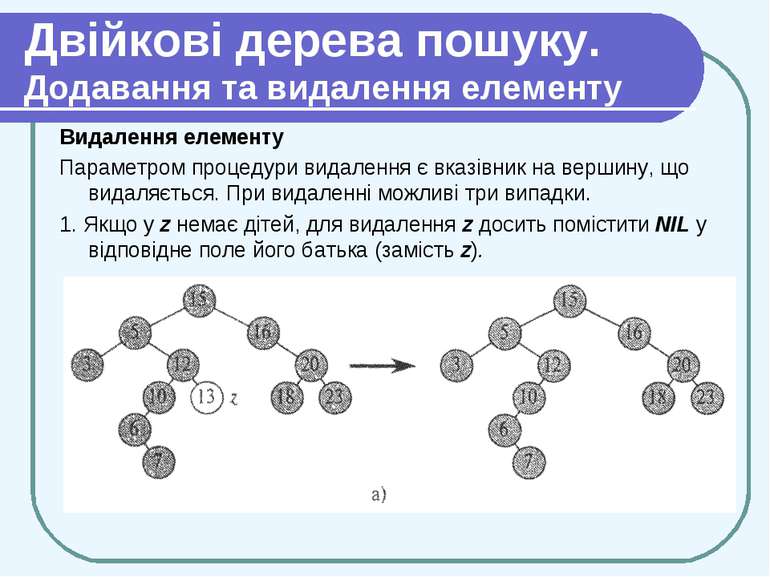
Двійкові дерева пошуку. Додавання та видалення елементу Видалення елементу Параметром процедури видалення є вказівник на вершину, що видаляється. При видаленні можливі три випадки. 1. Якщо у z немає дітей, для видалення z досить помістити NIL у відповідне поле його батька (замість z).

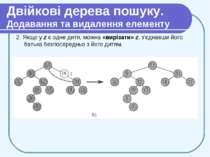
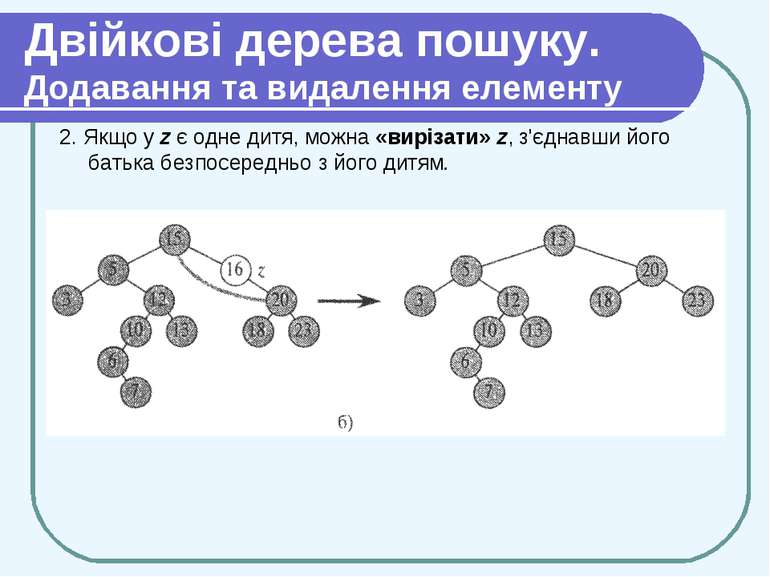
Двійкові дерева пошуку. Додавання та видалення елементу 2. Якщо у z є одне дитя, можна «вирізати» z, з'єднавши його батька безпосередньо з його дитям.

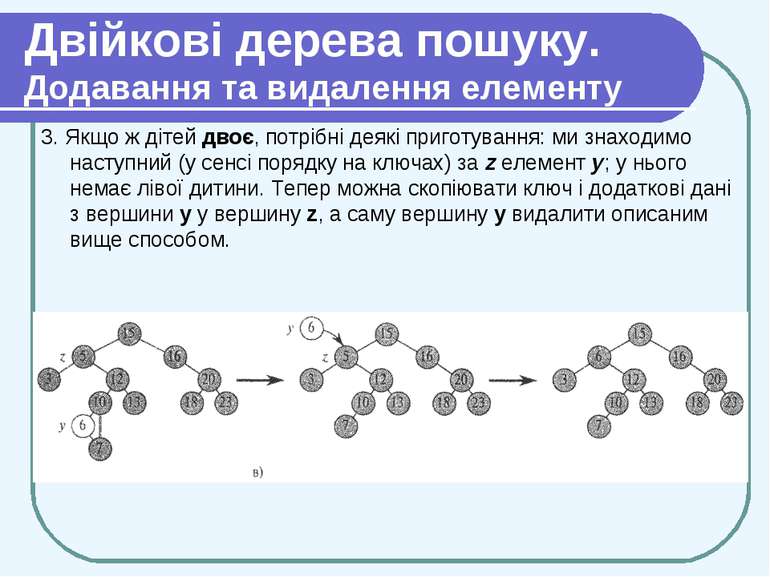
Двійкові дерева пошуку. Додавання та видалення елементу 3. Якщо ж дітей двоє, потрібні деякі приготування: ми знаходимо наступний (у сенсі порядку на ключах) за z елемент у; у нього немає лівої дитини. Тепер можна скопіювати ключ і додаткові дані з вершини у у вершину z, а саму вершину у видалити описаним вище способом.

Двійкові дерева пошуку. Додавання та видалення елементу У ряд. 1-3 визн. вершина у, яку потім виріжемо з дерева. Це або сама вершина z (якщо у z не більше однієї дитини), або наступний за z елемент (якщо у z двоє дітей). У ряд. 4-6 змінна x стає вказівником на існуючу дитину вершини у, або рівною NIL, якщо у у немає дітей. У рядках 7-13 вершина у вирізається з дерева (міняються вказівники в вершинах р[у] і x). Окремо розглядаються граничні випадки, коли x = NIL і коли у є коренем дерева. У рядках 14-16, якщо вирізана вершина у відмінна від z, ключ (і додаткові дані) вершини у переміщаються в z (адже нам треба було видалити z, а не у). Нарешті, процедура повертає вказівник у (це дозволить викликаючій процедурі згодом звільнити пам'ять, зайняту вершиною у).

Двійкові дерева пошуку. Додавання та видалення елементу Таким чином, операції Insert і Delete можуть бути виконані за час O(h), де h — висота дерева.

БАЖАЮ УСПІХІВ!!!