Презентація на тему:
Графіки і діаграми навколо нас

«Графіки і діаграми навколо нас» Підготував учень 10-А класу Барченков Роман

“ Книга природи написана математичною мовою і її букви - математичні знаки й геометричні фігури, без них неможливо зрозуміти її слова, без них марне блукання в нескінченному лабіринті ”. Г.Галілей

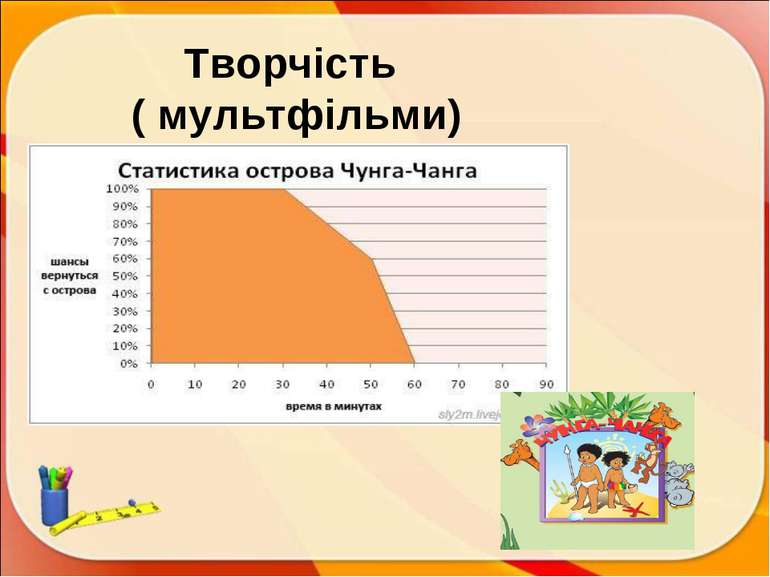
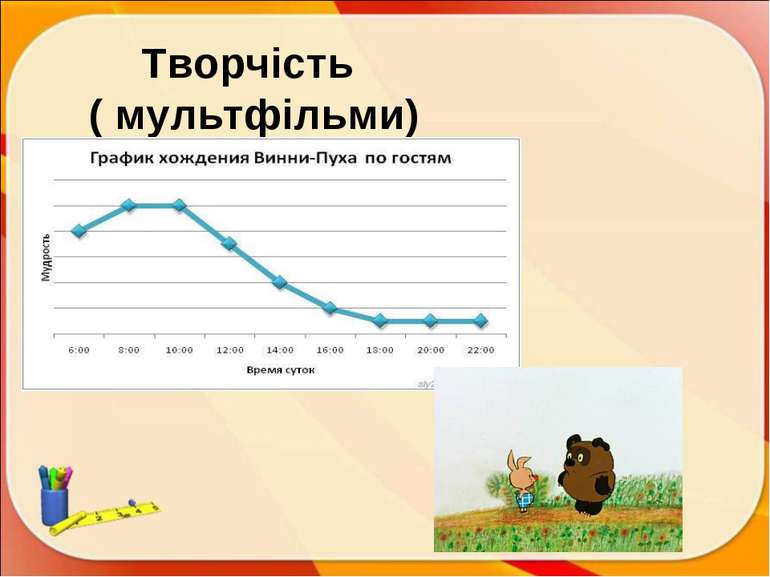
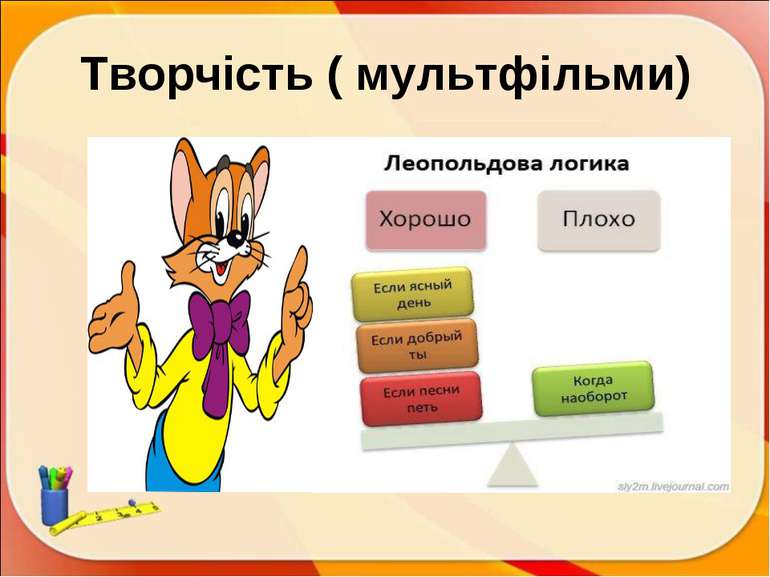
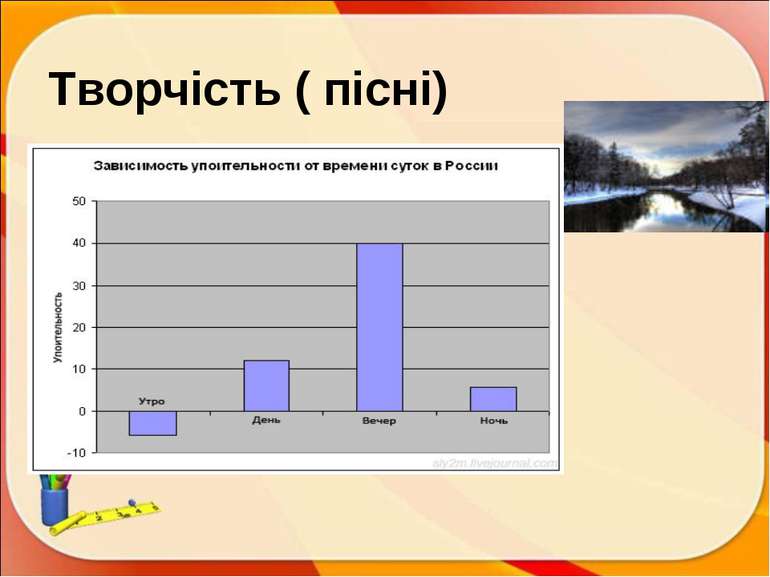
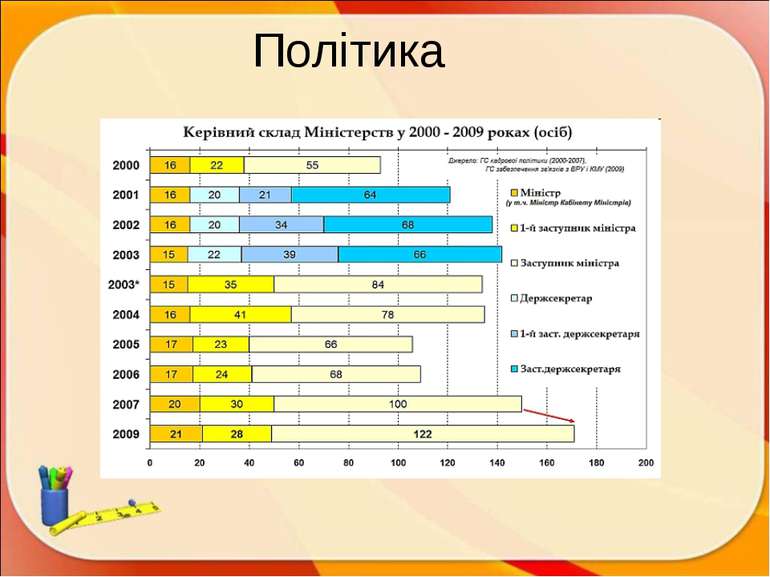
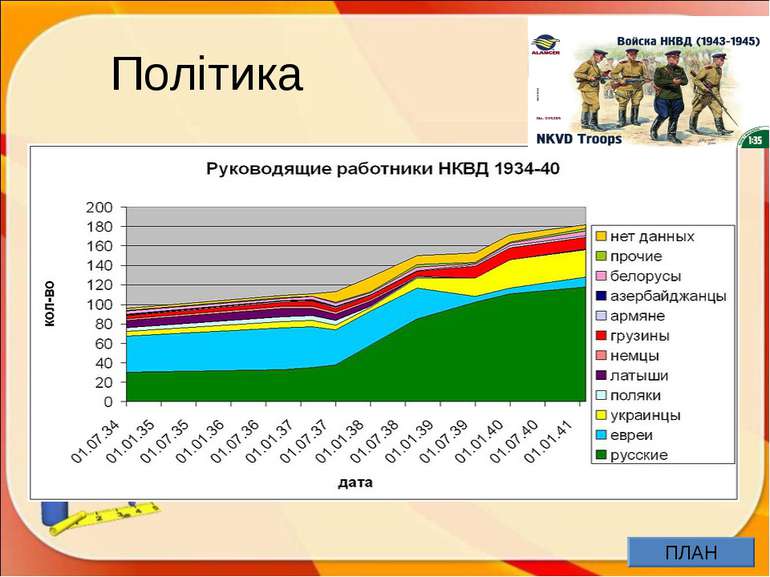
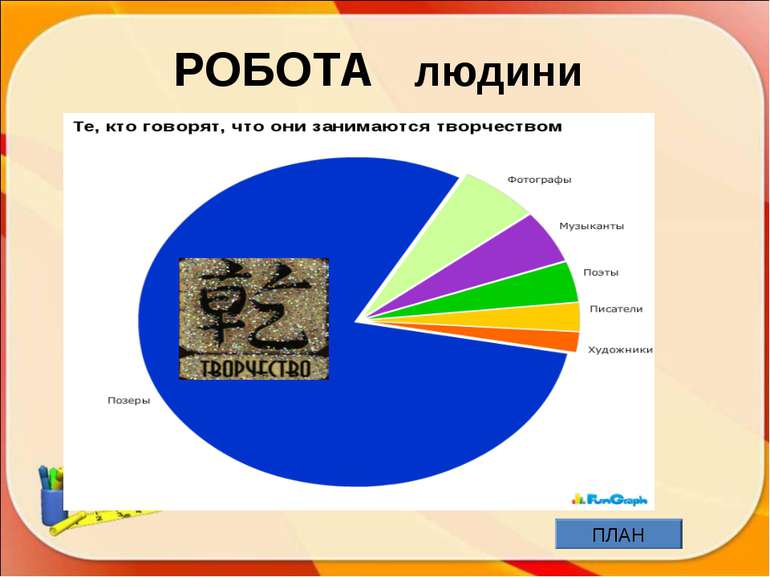
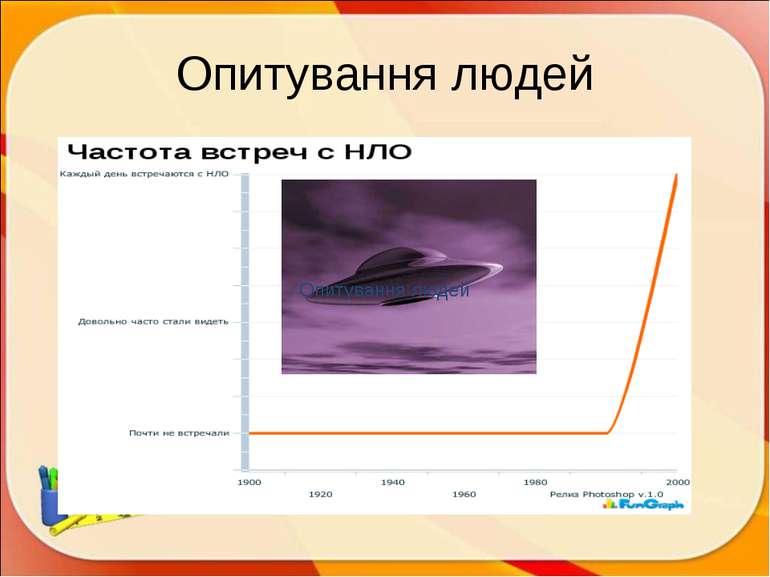
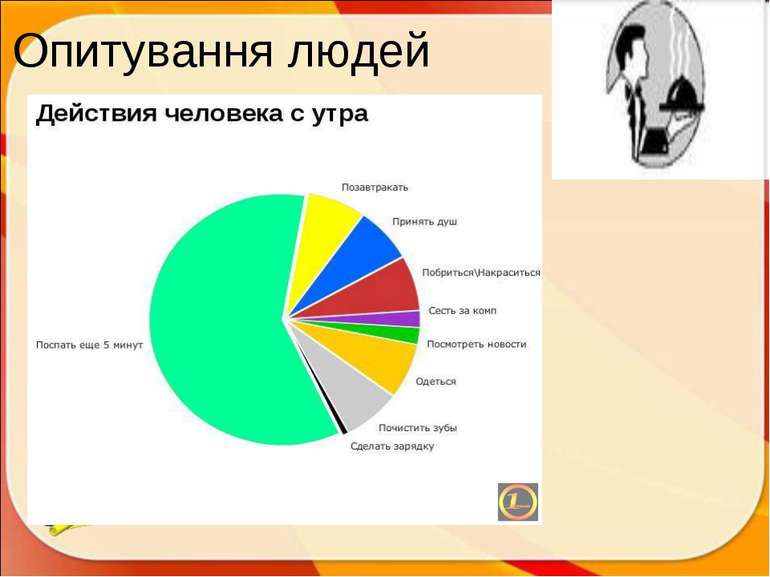
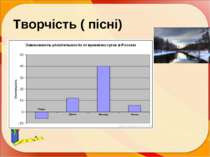
ПЛАН Історична довідка. Означення Вивчені графіки і діаграми. Цікаві графіки. Застосування в житті: медицина; харчування; робота; політика; творчість (музика, пісні, казки, прислів’я, мультики, кінофільми); у статистиці ; комп’ютери; тварини Задачі

Історична довідка П. Ферма (1601—1665), Р. Декарт (1596—1650) - помітили, що введення системи координат на площини і завдання фігур їхніми рівняннями дозволяють звести багато задач геометрії до дослідження рівнянь геометричних фігур

Історична довідка И. Ньютон (1643—1727), Г. В. Лейбніц (1646—1716). - досліджуючи залежності координат точки, що рухається, від часу, фактично вже займався дослідженням функцій - термін «функція» уперше зустрічається в його рукописі , а потім і в друкованому вигляді. Увів це поняття для назви різних параметрів, зв’язаних з положенням точки на площині

Історична довідка И. Бернуллі (1667—1748)    Л. Эйлер поступово приходять до розуміння функції як аналітичного виразу й дає таке означення: «Функцією змінної величини називається кількість, складена яким завгодно способом з цієї перемінної і постійних». -сформулював означення функції так: «Функція перемінної кількості є аналітичне вираження, складене яким-небудь способом з цієї перемінної кількості і чисел чи постійних кількостей». Ввів позначення для функцій.

Історична довідка Н. И. Лобачевский (1834 р.) Л. Діріхле (1837 р.). ідея їх визначень функції полягала в наступному: не істотно, яким образом ( необов’язково шляхом завдання аналітичного вираження) кожному поставлено у відповідність визначене значення, важливо тільки, що ця відповідність установлена.

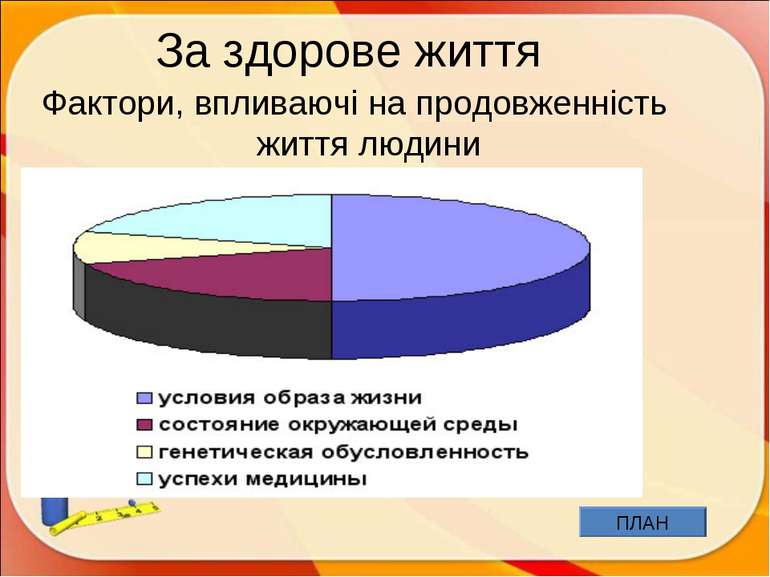
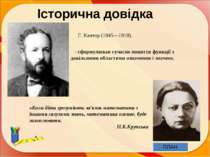
Історична довідка Г. Кантор (1845—1918). «Коли діти зрозуміють зв'язок математики з іншими галузями знань, математика оживе, буде захоплювати. Н.К.Крупська    - сформулював сучасне поняття функції з довільними областями означення і значень ПЛАН

Означення функції: Функція – залежність змінної y від змінної x, при якій кожному значенню x відповідає єдине значення y. y = f(х), де х- незалежна змінна або аргумент, а у - залежна змінна

Приклади залежностей в житті Шлях, який проїде машина з постійною швидкістю і часом руху. Площа квадрата і довжина сторони Ціною товару і кількістю, купленої за однією ціною. Віком людини і розміром його взуття

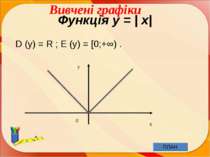
Для функції знаходять: Область означення функції – всі значення, які приймає незалежна змінна. Позначається : D (f). Область (множина) значень функції – всі значення, які приймає залежна змінна. Позначається : E (f).

Способи задання функції 1.Формулою у = 3х-15 2.Таблицею 3. Графічним способом ( діаграмою або графіком) х -2 -1 0 3 у 5 7 -3 -5

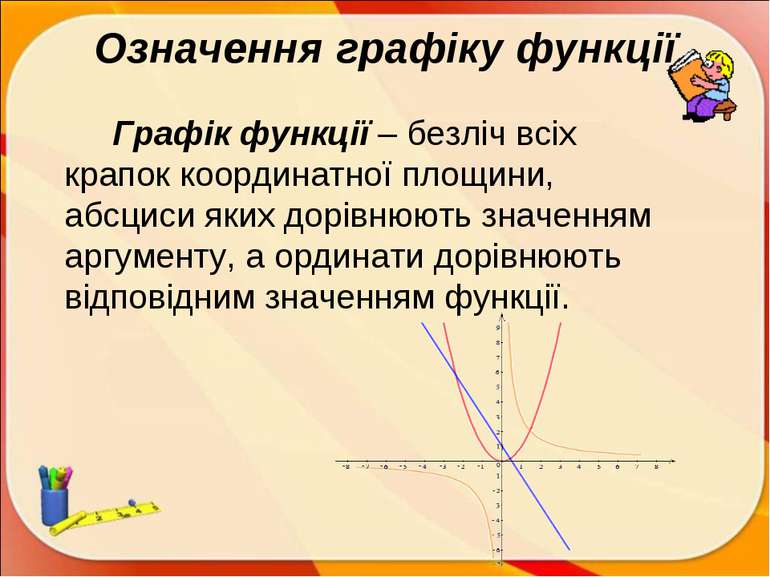
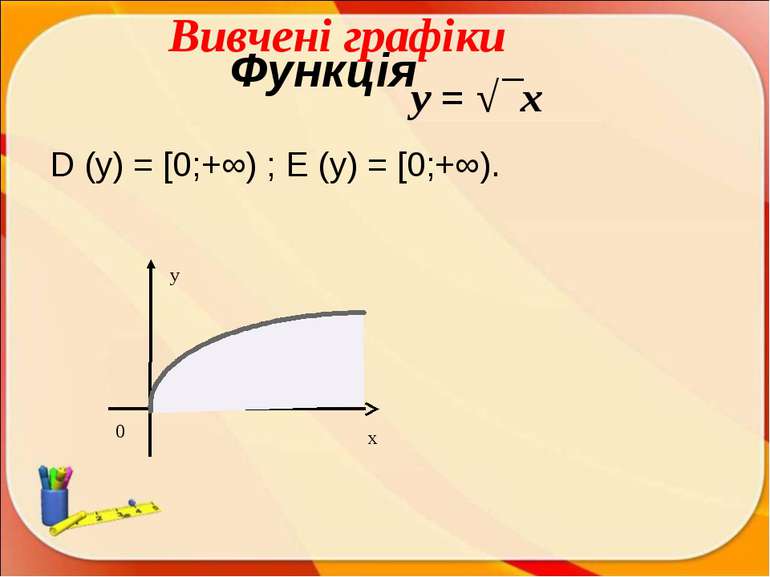
Означення графіку функції Графік функції – безліч всіх крапок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати дорівнюють відповідним значенням функції.

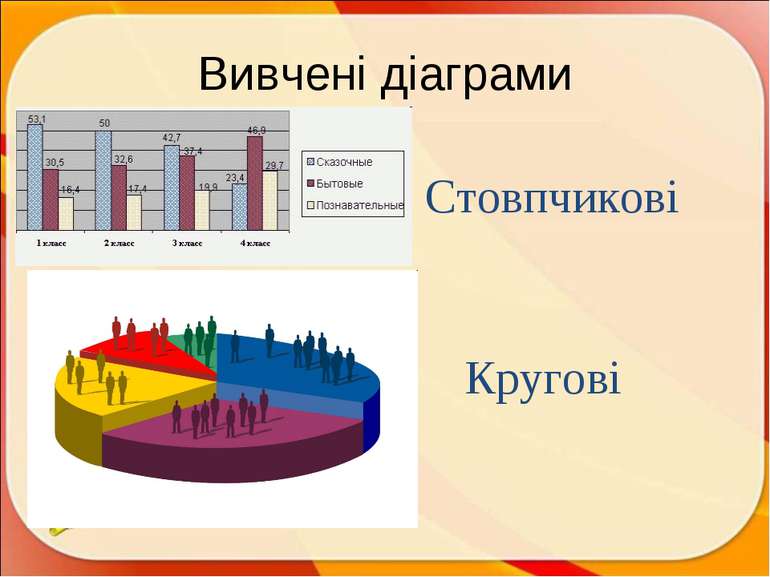
Означення діаграми Діаграма в перекладі із грецького позначає «зображення», «малюнок», «креслення». Діаграма - це графічне зображення у вигляді лінійних відрізків або геометричних фігур, що наочно показує співвідношення яких-небудь величин. Діаграма – це креслення або схема, що наочно показує співвідношення між різними величинами. ПЛАН

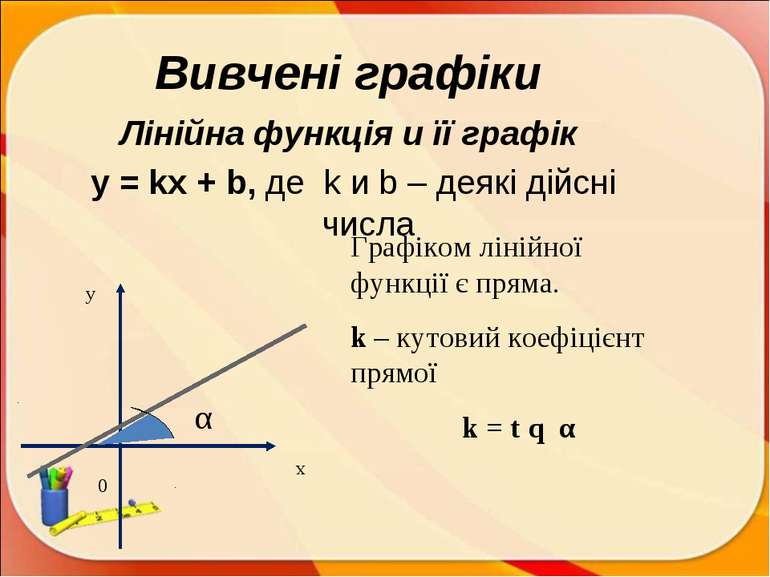
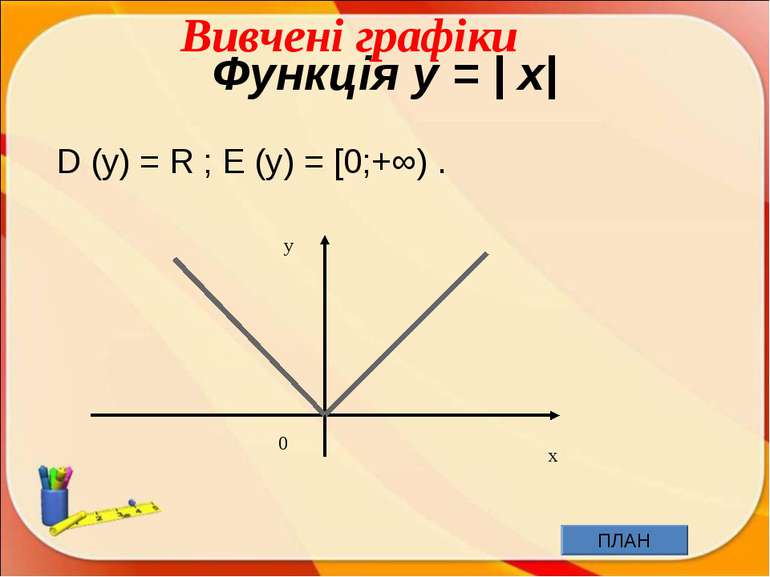
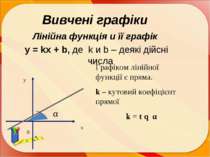
Вивчені графіки Лінійна функція и її графік y = kx + b, де k и b – деякі дійсні числа х у Графіком лінійної функції є пряма. k – кутовий коефіцієнт прямої k = t q α 0 α

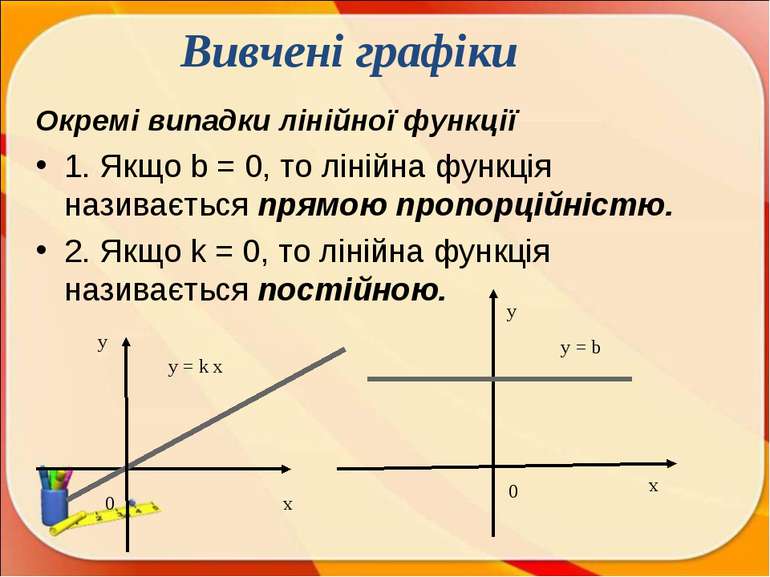
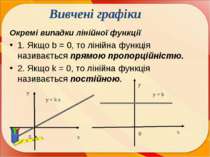
Окремі випадки лінійної функції 1. Якщо b = 0, то лінійна функція називається прямою пропорційністю. 2. Якщо k = 0, то лінійна функція називається постійною. у х у = k х y = b у х 0 0 Вивчені графіки

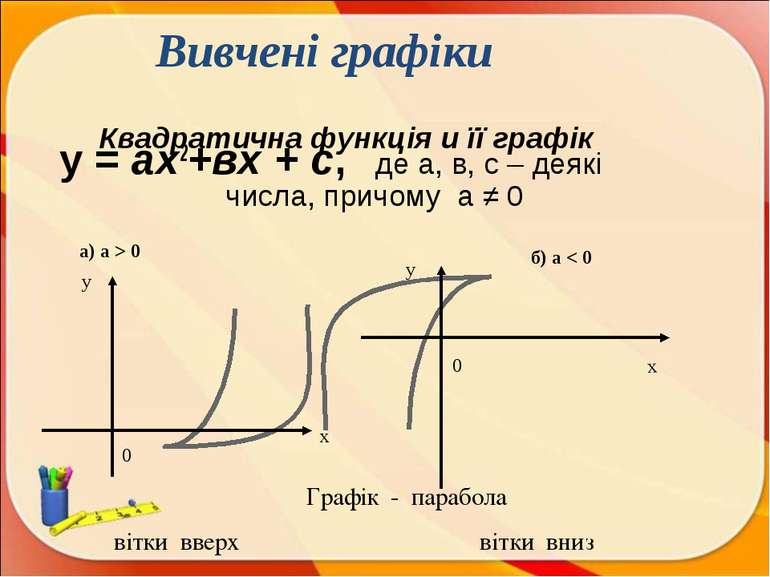
Квадратична функція и її графік у = ах2+вх + с, де а, в, с – деякі числа, причому а ≠ 0 а) а > 0 б) а < 0 Графік - парабола вітки вверх вітки вниз 0 0 Вивчені графіки

Вивчені діаграми Стовпчикові Кругові

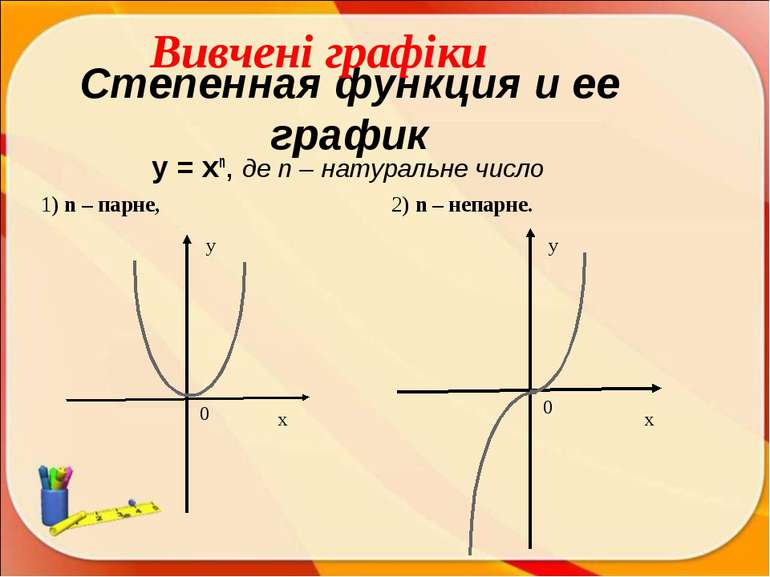
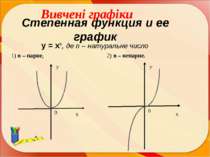
Степенная функция и ее график y = xn, де n – натуральне число 1) n – парне, 2) n – непарне. х у х у 0 0 Вивчені графіки

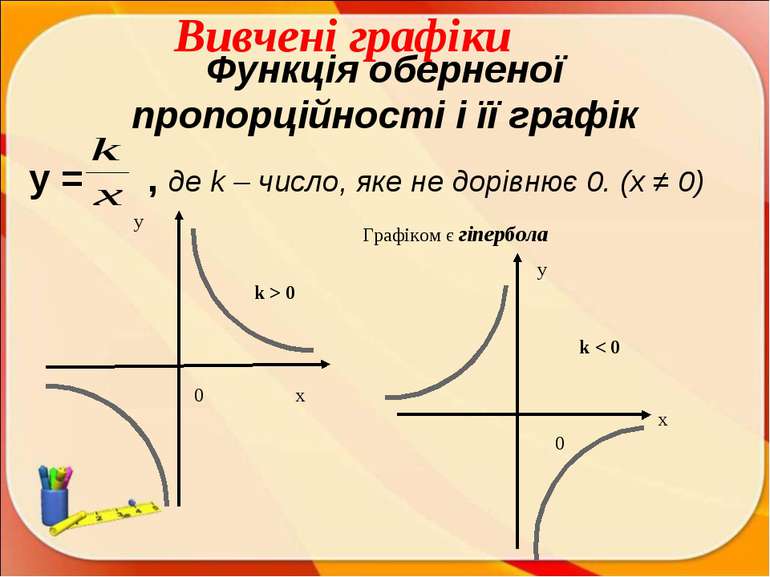
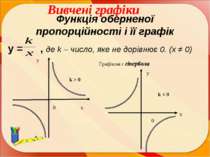
Функція оберненої пропорційності і її графік y = , де k – число, яке не дорівнює 0. (x ≠ 0) у Графіком є гіпербола k > 0 k < 0 х х у 0 0 Вивчені графіки

Функція D (y) = [0;+∞) ; E (y) = [0;+∞). y = √¯x x y 0 Вивчені графіки

Функція y = | x| D (y) = R ; E (y) = [0;+∞) . x y 0 Вивчені графіки ПЛАН

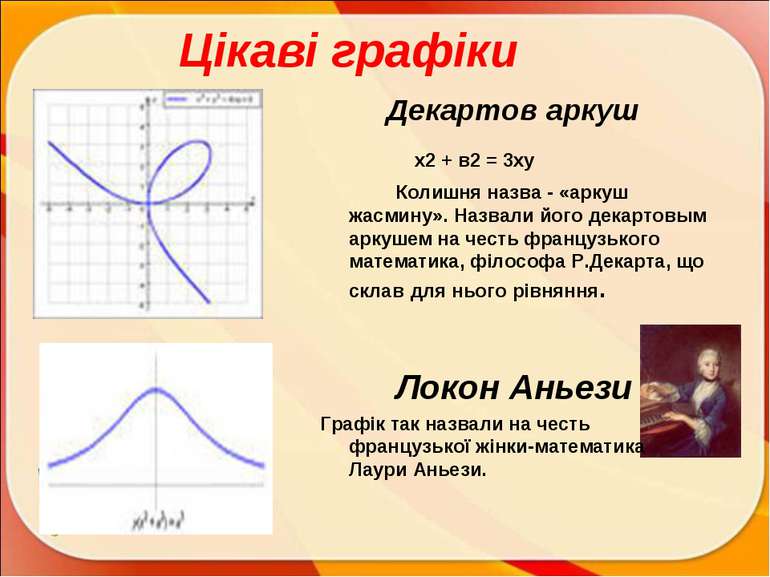
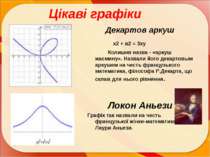
Цікаві графіки Декартов аркуш х2 + в2 = 3ху Колишня назва - «аркуш жасмину». Назвали його декартовым аркушем на честь французького математика, філософа Р.Декарта, що склав для нього рівняння. Локон Аньези Графік так назвали на честь французької жінки-математика Лаури Аньези.

Цікаві графіки Клофоіда (спіраль Кореню) «Клофо» - від гречок. «прясти». Клофоіда більше знайома залізничникам як радиоидальная спіраль. По рівнянню клофоиды вони розраховують, у якій крапці виявиться поїзд, пройшовши по клофоиде яка-небудь відстань. Лемніската Бернуллі Теж відома залізничникам-інженерам. Вона служить перехідною лінією між ділянками залізничного полотна прямолінійної й округлої форми, забезпечуючи плавність закруглення. Кардіоїд - має форму серця. ПЛАН

За здорове життя

За здорове життя

За здорове життя

За здорове життя

За здорове життя Фактори, впливаючі на продовженність життя людини ПЛАН

Комп’ютер і ми

Комп’ютер і ми

Комп’ютер і ми

Комп’ютер і ми ПЛАН

Із життя котів

Із життя котів ПЛАН

Медицина ПЛАН

Творчість ( музика)

Творчість ( фільми)

Творчість ( фільми)

Творчість ( фільми)

Творчість ( мультфільми)

Творчість ( фільми)

Творчість ( фільми)

Творчість ( мультфільми)

Творчість ( мультфільми)

Творчість ( мультфільми)

Творчість ( мультфільми)

Творчість ( фільми)

Творчість ( пісні)

Творчість ( пісні)

Творчість ( пісні)

Творчість ( пісні)

Творчість ( пісні)

Творчість ( пісні)

Творчість ( пісні) « Владимирский централ – ветер северный…»

Твочість ( кінофільми та мультфільми)

Прислів’я та приказки “ Голод не тетка, в лес не убежит”

Прислів’я та приказки “ Старый друг лучше новых двух”

Прислів’я та приказки “ Сколько волка не корми, он все равно в лес смотрит”

Прислів’я та приказки “ Муж и жена – одна сатана”

Прислів’я та приказки “ Семь раз отмерь , один раз отрежь”

Прислів’я та приказки “ Хрен редьки не слаще”

Прислів’я та приказки “ КПСС - ум, честь и совесть нашей епохи”

Прислів’я та приказки “ Делу – время, потехе – час” ПЛАН

Політика

Політика

Політика

Політика

Політика ПЛАН

РОБОТА людини

РОБОТА людини ПЛАН

Опитування людей

Опитування людей Опитування людей

Опитування людей

Опитування людей

Опитування людей

Опитування людей

Опитування людей

Опитування людей ПЛАН

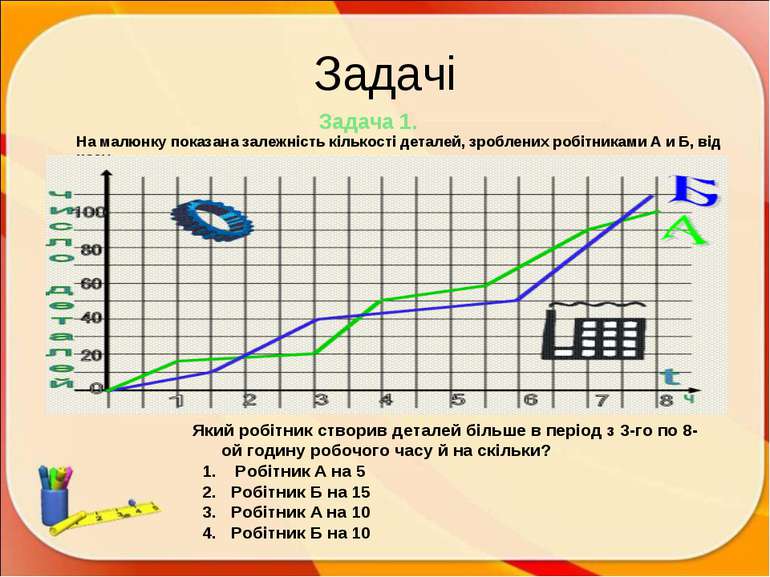
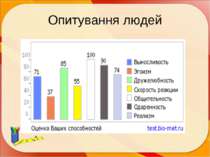
Задачі Задача 1. На малюнку показана залежність кількості деталей, зроблених робітниками А и Б, від часу. Який робітник створив деталей більше в період з 3-го по 8-ой годину робочого часу й на скільки?   1.    Робітник А на 5   2.   Робітник Б на 15   3.   Робітник А на 10   4.   Робітник Б на 10

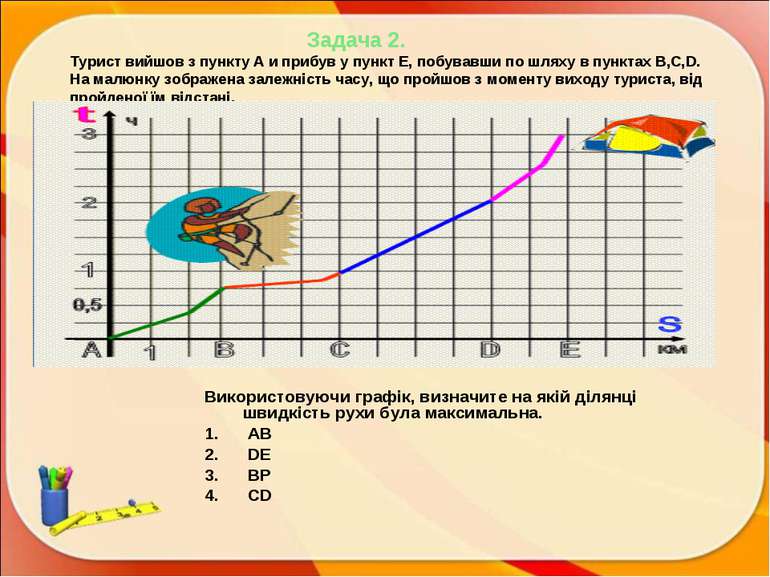
Задача 2. Турист вийшов з пункту А и прибув у пункт Е, побувавши по шляху в пунктах B,C,D. На малюнку зображена залежність часу, що пройшов з моменту виходу туриста, від пройденої їм відстані. Використовуючи графік, визначите на якій ділянці швидкість рухи була максимальна.  АВ  DE  ВР  СD

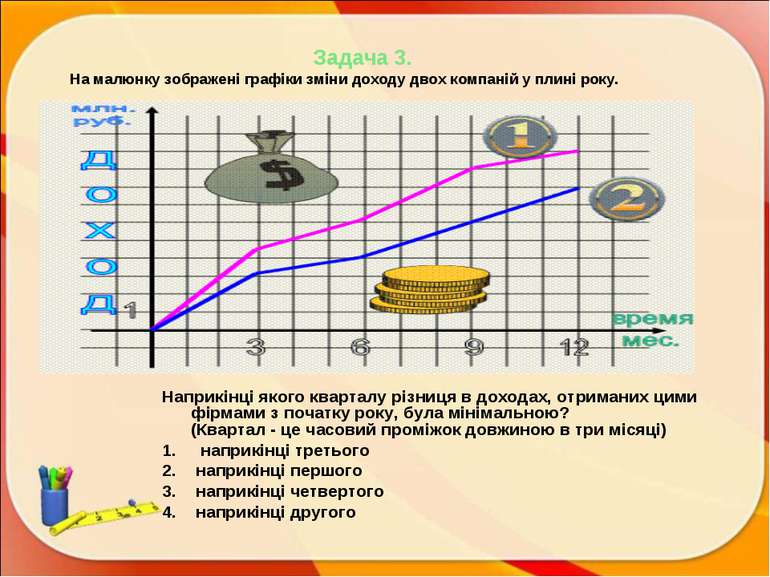
Задача 3. На малюнку зображені графіки зміни доходу двох компаній у плині року. Наприкінці якого кварталу різниця в доходах, отриманих цими фірмами з початку року, була мінімальною? (Квартал - це часовий проміжок довжиною в три місяці)   наприкінці третього  наприкінці першого  наприкінці четвертого  наприкінці другого

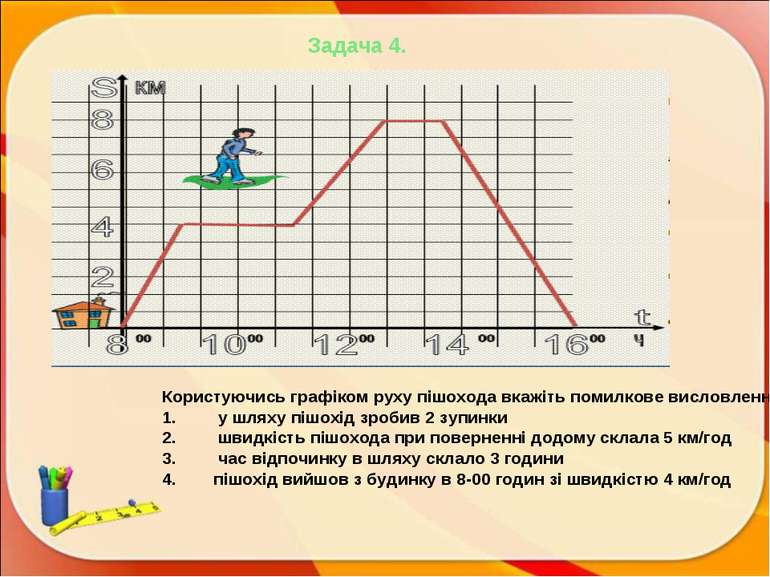
Задача 4. Користуючись графіком руху пішохода вкажіть помилкове висловлення  у шляху пішохід зробив 2 зупинки  швидкість пішохода при поверненні додому склала 5 км/год  час відпочинку в шляху склало 3 години пішохід вийшов з будинку в 8-00 годин зі швидкістю 4 км/год

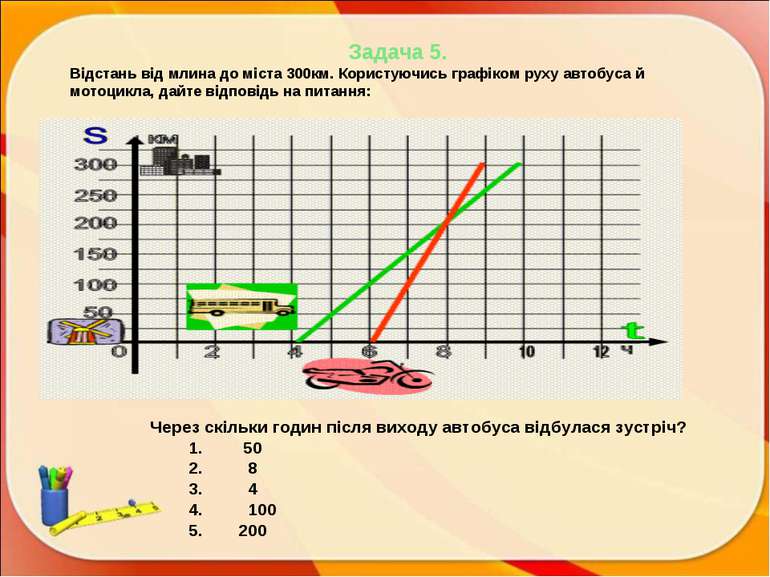
Задача 5. Відстань від млина до міста 300км. Користуючись графіком руху автобуса й мотоцикла, дайте відповідь на питання: Через скільки годин після виходу автобуса відбулася зустріч?   50    8    4    100  200

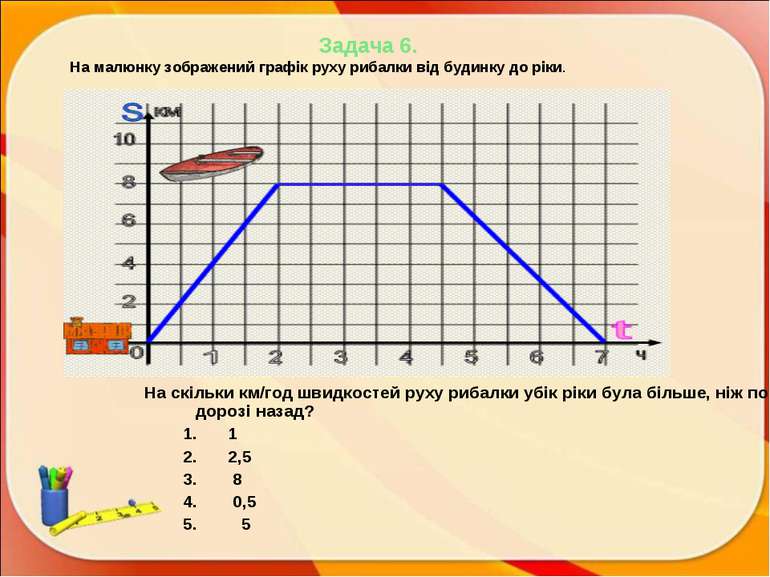
Задача 6. На малюнку зображений графік руху рибалки від будинку до ріки. На скільки км/год швидкостей руху рибалки убік ріки була більше, ніж по дорозі назад? 1 2,5  8  0,5    5

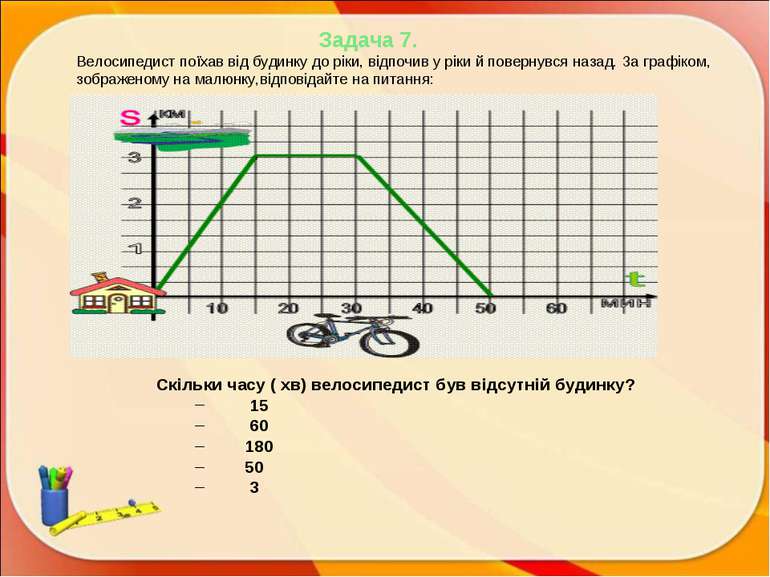
Задача 7. Велосипедист поїхав від будинку до ріки, відпочив у ріки й повернувся назад. За графіком, зображеному на малюнку,відповідайте на питання: Скільки часу ( хв) велосипедист був відсутній будинку?   15   60  180  50   3

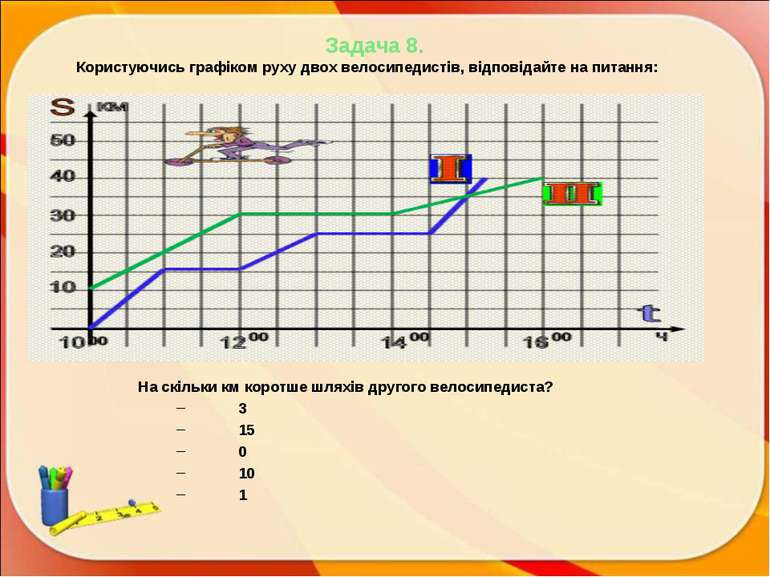
Задача 8. Користуючись графіком руху двох велосипедистів, відповідайте на питання: На скільки км коротше шляхів другого велосипедиста?     3     15     0     10     1

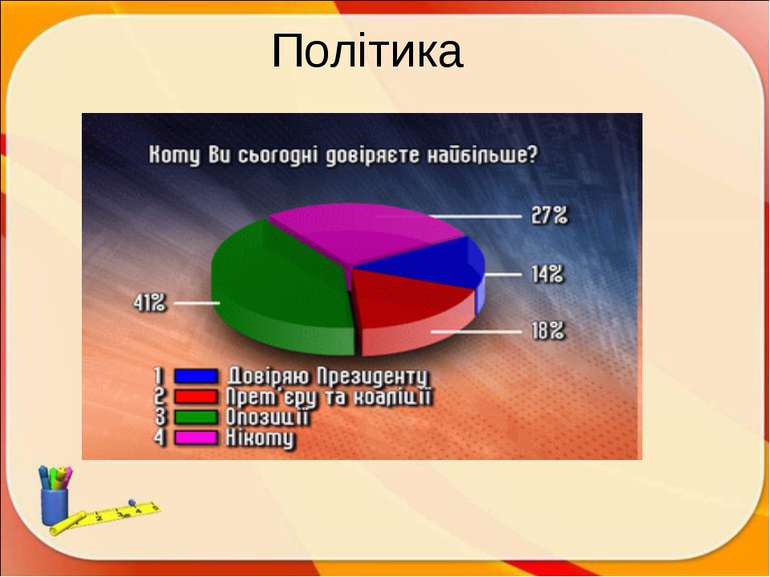
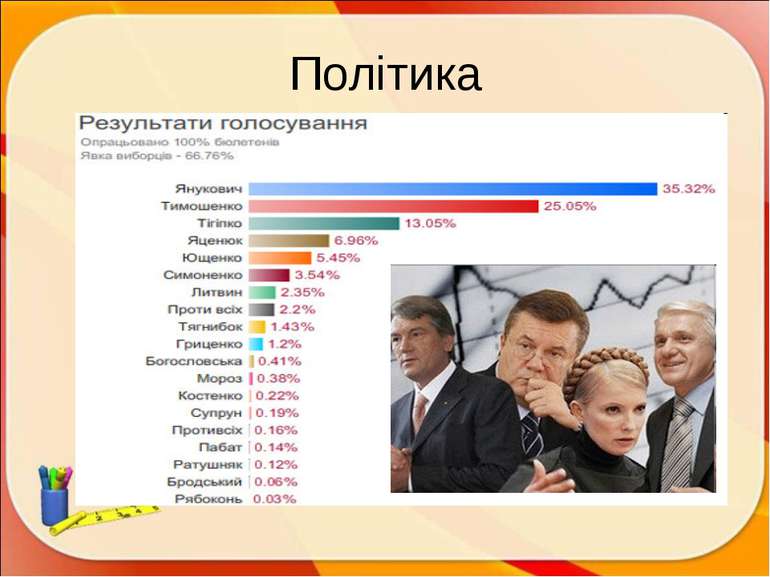
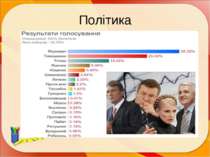
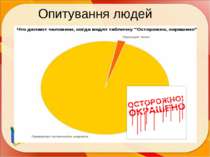
Задача 9. Відповідайте по малюнку на наступні питання: Скільки % голосів набрав кожний з кандидатів? Хто з кандидатів не має шансів на перемогу у виборах у місті NN? В II турі виборів мають право брати участь не більше двох кандидатів, що набрали в першому турі найбільша кількість голосів виборців. Хто з кандидатів має право брати участь в II турі виборів?

Задача 10. За статутом міста До мером міста обирається той кандидат, що у першому турі голосування набрав більше 50% голосів виборців. Якщо ніхто з кандидатів не набрав більше половини голосів, призначається другий тур, куди виходять два кандидати, що набрали в першому турі більшість голосів. У другому турі перемагає той кандидат, хто набере більшість голосів. Після першого тура в газеті «Вісник міста ДО» була наведена діаграма голосування Аналізуючи цю діаграму, відповідайте на питання: Хто з кандидатів набрав в I турі найбільше число голосів? Хто з кандидатів набрав найменше число голосів? Чи буде призначені II тур і якщо так хто з кандидатів туди ввійде? Чи можна припустити хто виграє вибори в другому турі? ПЛАН