Презентація на тему:
Поворот

Поворот Геометрія, 9 клас Т.М. Скічко

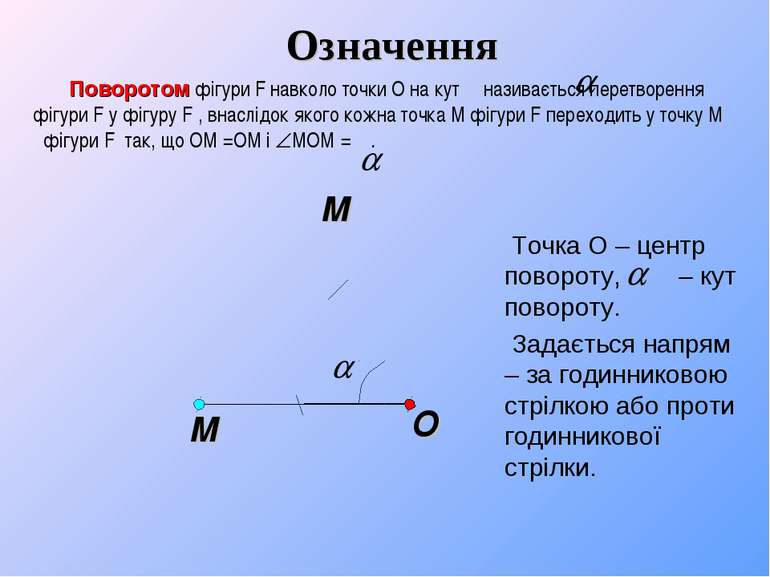
O Поворотом фігури F навколо точки О на кут називається перетворення фігури F у фігуру F′, внаслідок якого кожна точка M фігури F переходить у точку M′ фігури F′ так, що ОM′=ОM і MОM′= . М М′ Точка О – центр повороту, – кут повороту. Задається напрям – за годинниковою стрілкою або проти годинникової стрілки. Означення

Виконати поворот точки М на кут 60° М О М1

Виконати поворот відрізка на кут 90° O А В B’ А’ Сформулюйте алгоритм побудови

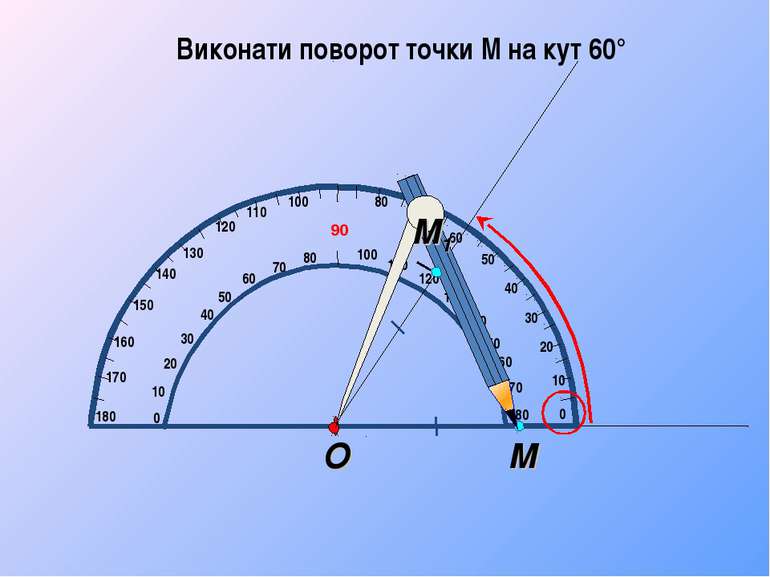
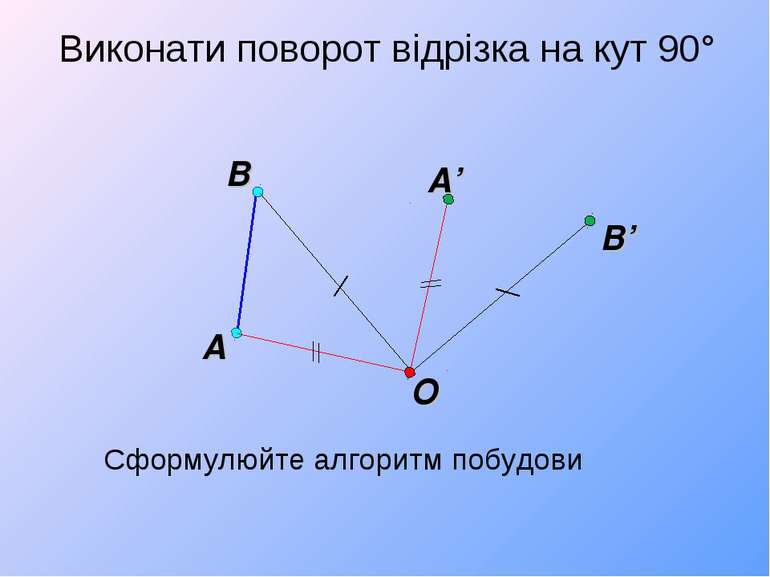
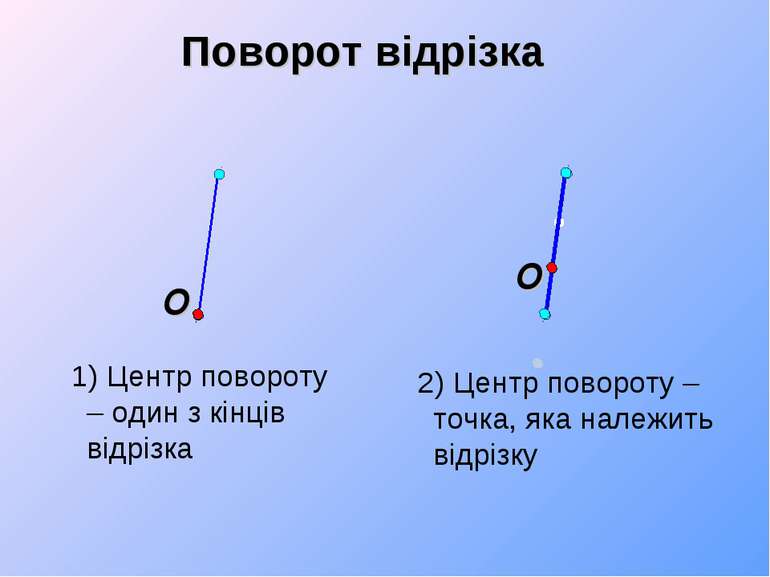
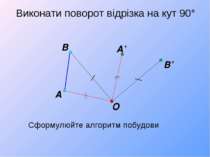
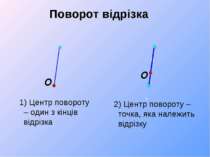
Поворот відрізка 1) Центр повороту – один з кінців відрізка 2) Центр повороту – точка, яка належить відрізку

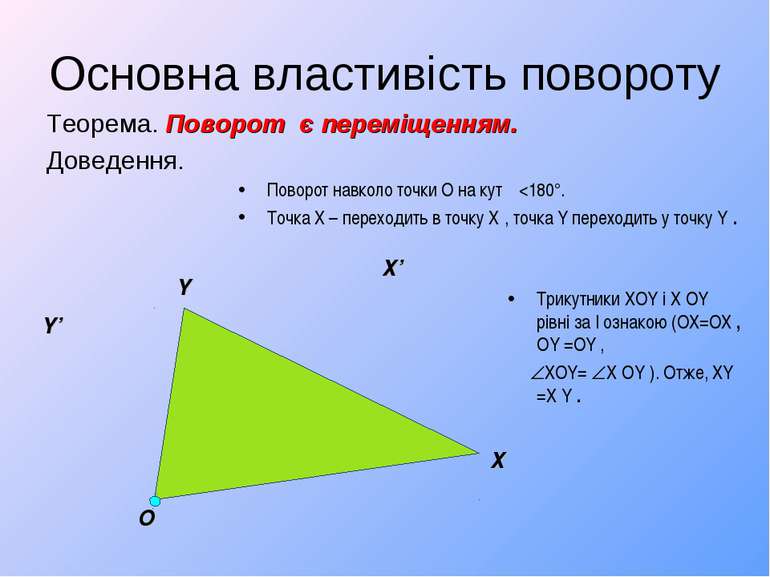
Основна властивість повороту Теорема. Поворот є переміщенням. Доведення. Поворот навколо точки О на кут α

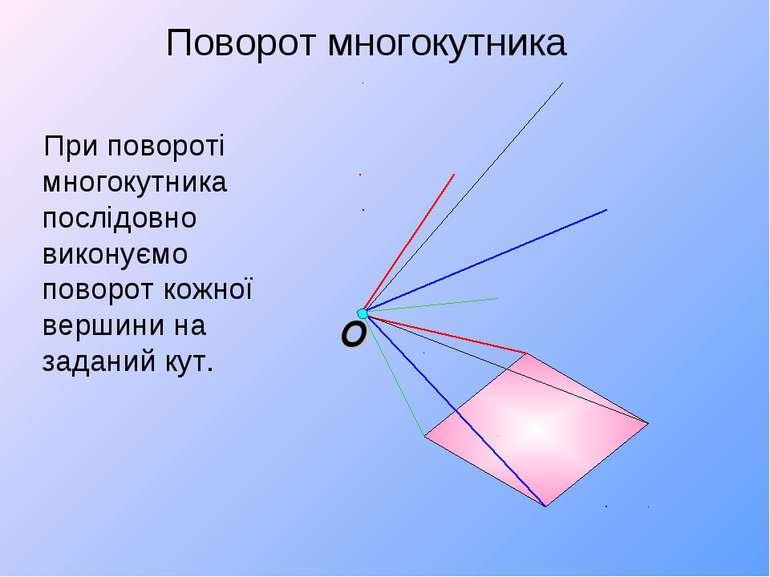
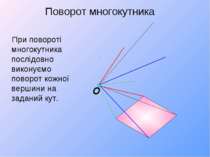
При повороті многокутника послідовно виконуємо поворот кожної вершини на заданий кут. Поворот многокутника

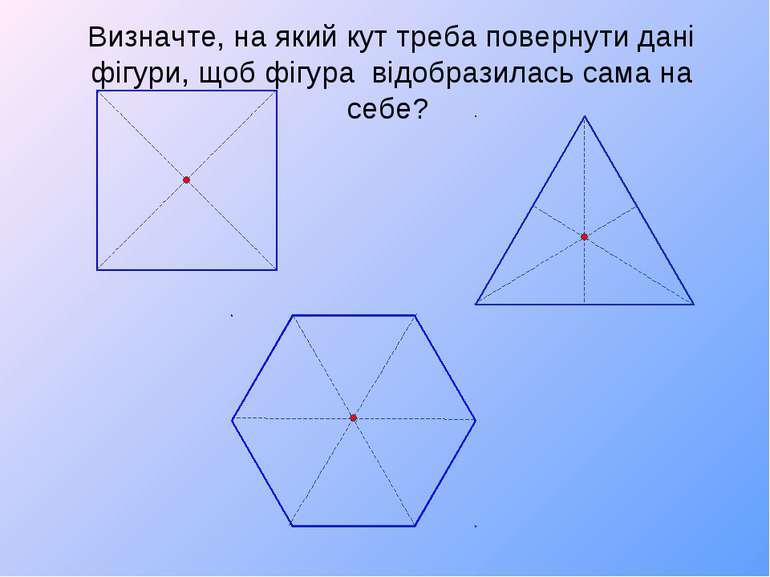
Симетрія обертання Якщо внаслідок повороту навколо деякої точки О на кут α (0°< α 180°) фігура F переходить у себе, то кажуть, що ця фігура має поворотну симетрію (або симетрію обертання).

Визначте, на який кут треба повернути дані фігури, щоб фігура відобразилась сама на себе?

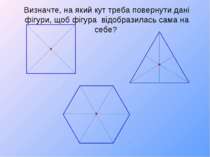
Властивості повороту: 1) Перетворення повороту є переміщенням. 2) Центральна симетрія є поворотом на 180°. 3) При повороті пряма переходить у пряму; кут – у рівний кут; відрізок – у рівний відрізок; будь-яка фігура переходить у рівну їй фігуру. 4) Правильний трикутник під час повороту навколо центра трикутника на 120° переходить у себе. Квадрат при повороті навколо центра квадрата на 90° (180°, 270°) переходить у себе. Правильний шестикутник при повороті навколо свого центра на 60° (120°, 180°, 240°, 270°) переходить у себе. Правильний многокутник при повороті навколо свого центра на кут переходить у себе.

5)Якщо точка В(х1; у1) є образом точки А(х; у) при повороті на 90° відносно початку координат: А) за годинниковою стрілкою, то виконується умова: х1=-у, у1=х; Б) проти годинникової стрілки, то виконується умова: х1= у, у1=-х. Властивості повороту:

Перевір себе. Яке переміщення називається поворотом? Сформулюйте властивості повороту.