Презентація на тему:
Паралелограми

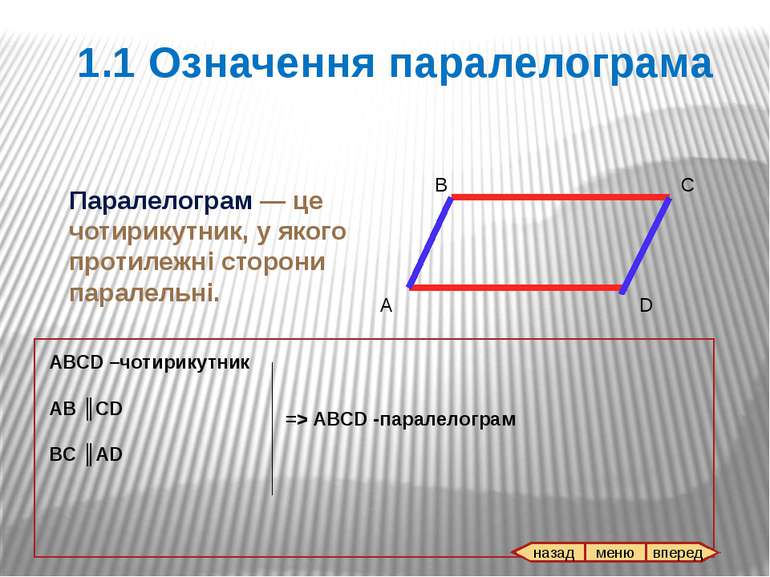
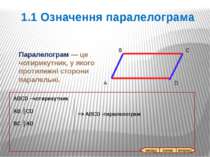
Паралелограм — це чотирикутник, у якого протилежні сторони паралельні. А В С D ABCD –чотирикутник AB ║CD BC ║AD => ABCD -паралелограм 1.1 Означення паралелограма назад

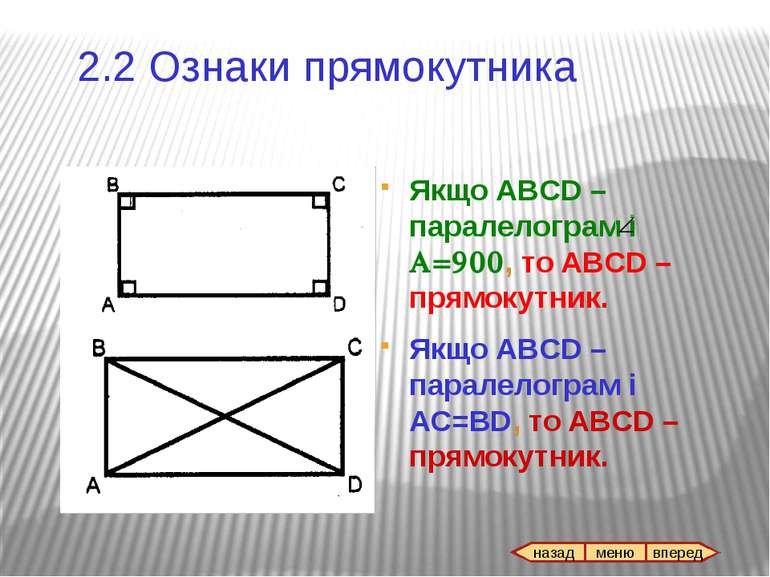
Якщо у чотирикутнику протилежні сторони паралельні і рівні, то цей чотирикутник паралелограм. D А В С ABCD – чотирикутник AB || CD AB = CD => ABCD- паралелограм 1.2 Ознаки паралелограма назад

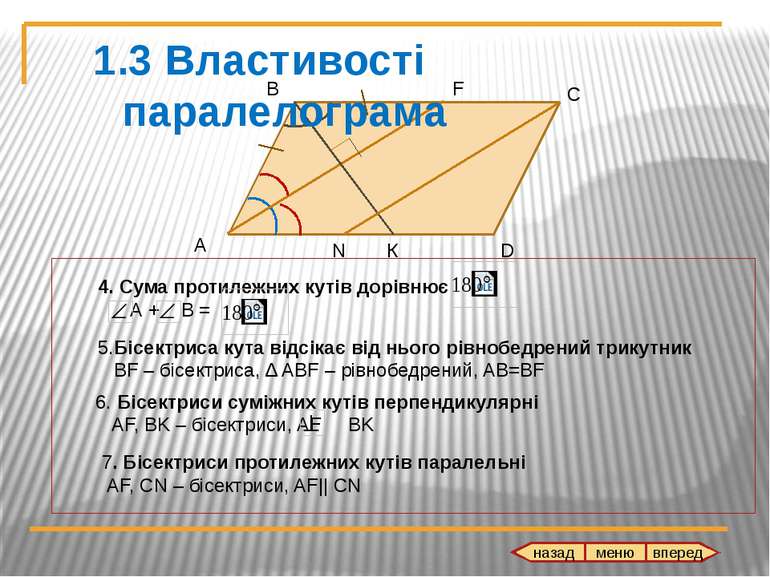
4. Сума протилежних кутів дорівнює А + В = А В С D 5.Бісектриса кута відсікає від нього рівнобедрений трикутник BF – бісектриса, ∆ ABF – рівнобедрений, AB=BF F 6. Бісектриси суміжних кутів перпендикулярні AF, BK – бісектриси, AF BK К 7. Бісектриси протилежних кутів паралельні AF, CN – бісектриси, AF|| CN N 1.3 Властивості паралелограма назад

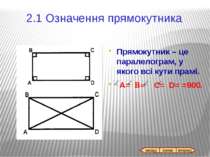
План Паралелограм. 1.1 Означення паралелограма 1.2 Ознаки паралелограма 1.3 Властивості паралелограма 2. Прямокутник 2.1 Означення прямокутника 2.2 Ознаки прямокутника 2.3 Властивості прямокутника 4. Ромб 4.1 Означення ромба 4.2 Ознаки ромба 4.3 Властивості ромба 3. Квадрат 3.1 Означення квадрата 3.2 Ознаки квадрата 3.3 Властивості квадрата

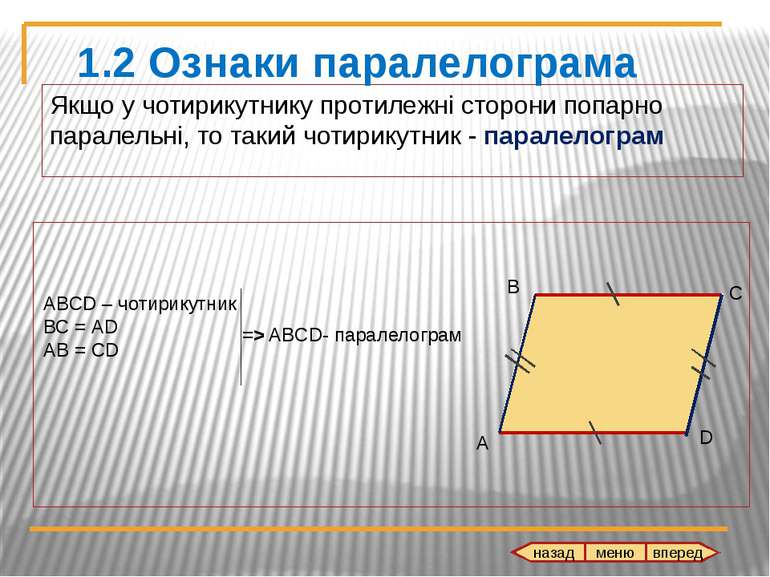
Якщо у чотирикутнику протилежні сторони попарно паралельні, то такий чотирикутник - паралелограм D А В С ABCD – чотирикутник ВС = АD AB = CD => ABCD- паралелограм 1.2 Ознаки паралелограма назад http://smiles.33bru.com/smile.bereich100_0.html

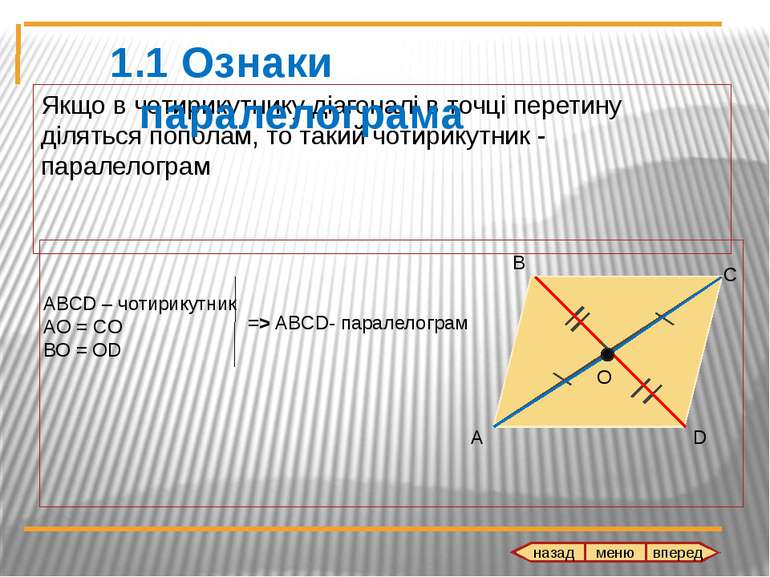
Якщо в чотирикутнику діагоналі в точці перетину діляться пополам, то такий чотирикутник - паралелограм D А В С ABCD – чотирикутник AО = CО ВО = ОD О => ABCD- паралелограм 1.1 Ознаки паралелограма назад

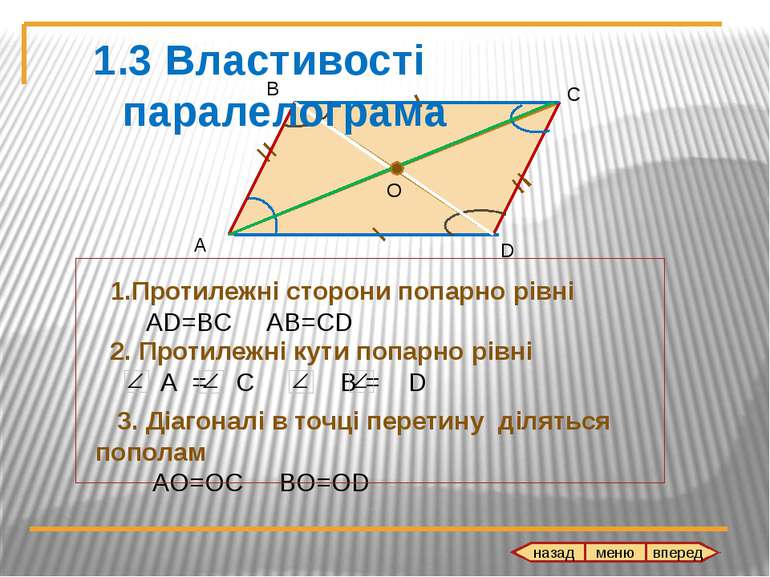
А В С D O 3. Діагоналі в точці перетину діляться пополам AO=OC BO=OD 1.Протилежні сторони попарно рівні AD=BC AB=CD 2. Протилежні кути попарно рівні А = С В = D 1.3 Властивості паралелограма назад

Якщо ABCD – чотирикутник і AB=AD=BC=CD, то ABCD – ромб. 3.2 Ознаки ромба назад

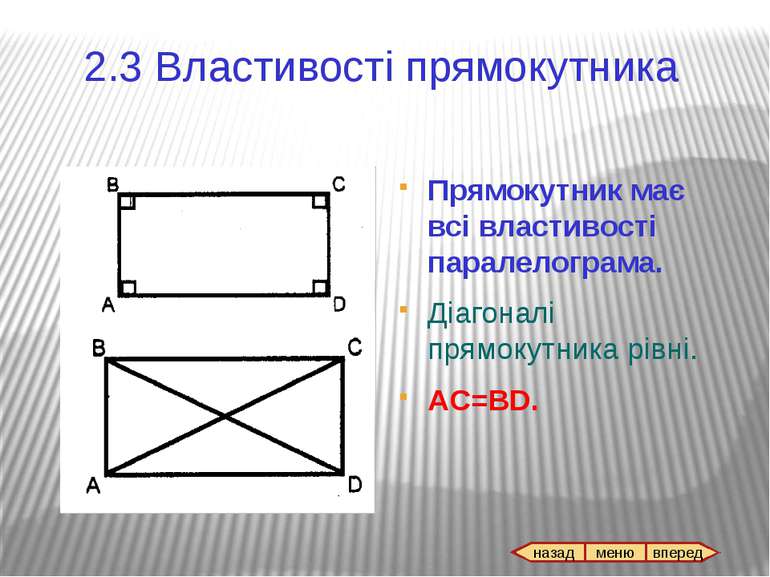
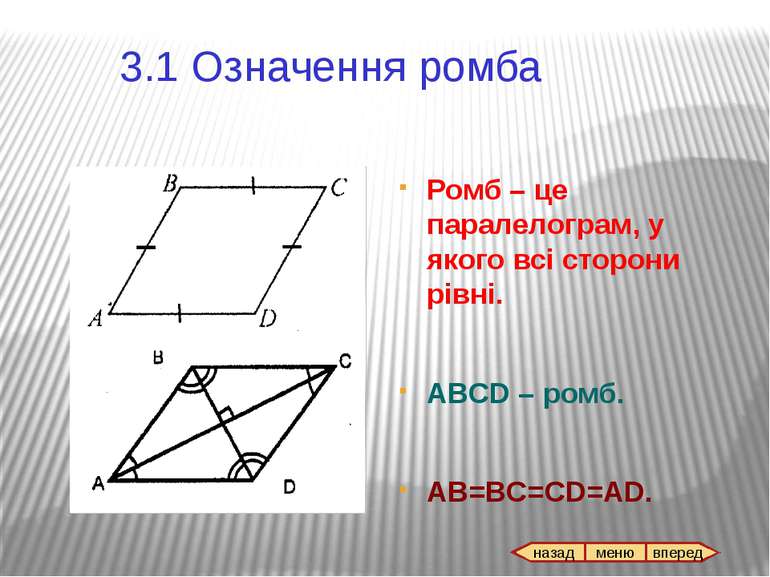
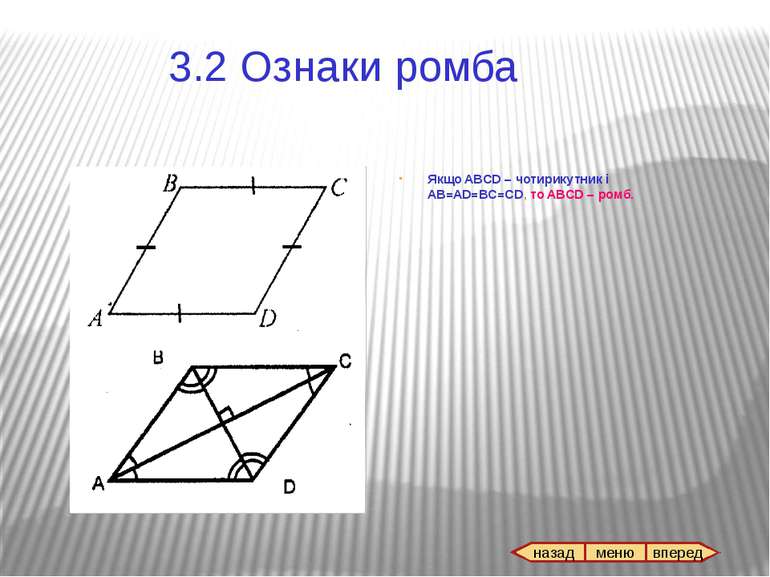
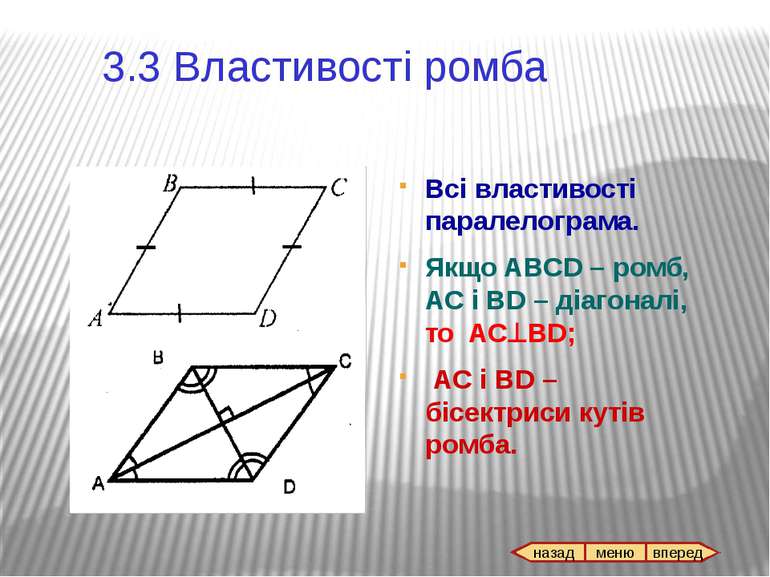
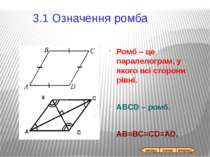
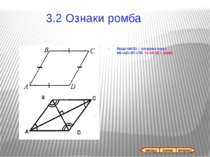
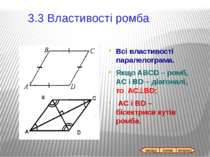
Всі властивості паралелограма. Якщо ABCD – ромб, АС і BD – діагоналі, то AC^BD; AC i BD – бісектриси кутів ромба. 3.3 Властивості ромба назад

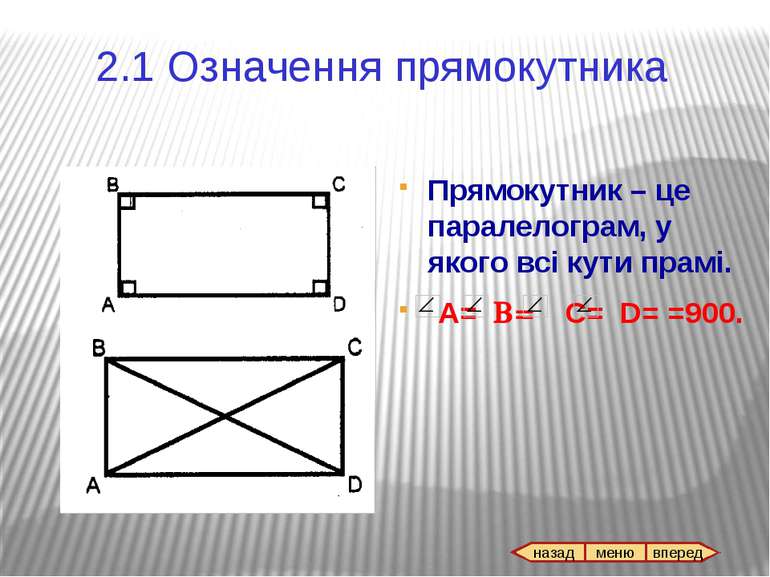
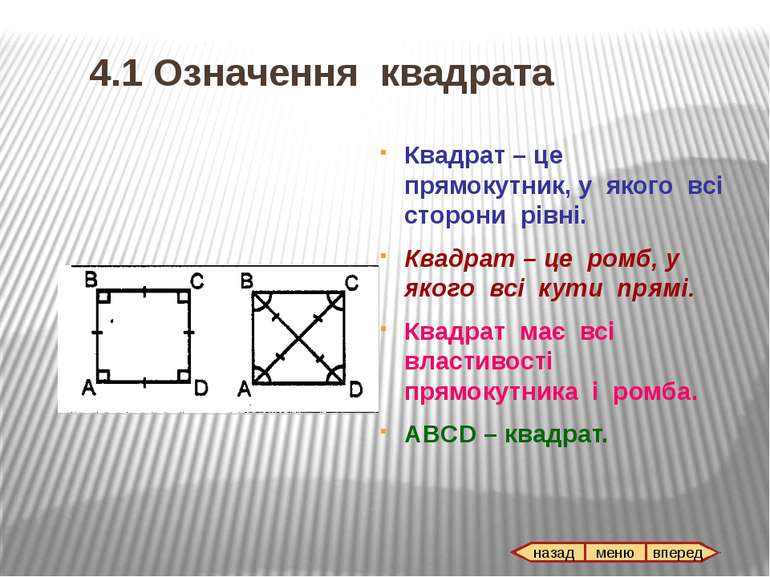
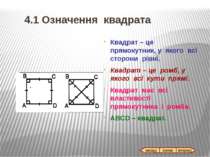
4.1 Означення квадрата Квадрат – це прямокутник, у якого всі сторони рівні. Квадрат – це ромб, у якого всі кути прямі. Квадрат має всі властивості прямокутника і ромба. ABCD – квадрат. назад

Якщо в чотирикутника всі сторони і всі кути рівні, то він є квадратом. ABCD – чотирикутник AB = CD=BC = AD => ABCD- квадрат 4.2 Ознаки квадрата А В С O D назад

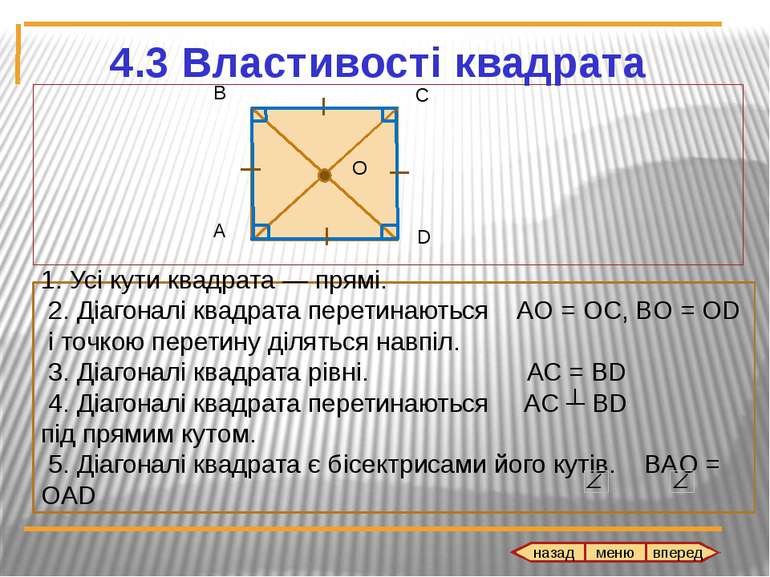
4.3 Властивості квадрата А В С O D 1. Усі кути квадрата — прямі. 2. Діагоналі квадрата перетинаються AO = OC, BO = OD і точкою перетину діляться навпіл. 3. Діагоналі квадрата рівні. АС = ВD 4. Діагоналі квадрата перетинаються AC ┴ BD під прямим кутом. 5. Діагоналі квадрата є бісектрисами його кутів. BAO = OAD назад

Якщо діагоналі прямокутника перетинаються під прямим кутом, то він є квадратом ABCD – чотирикутник AОВ= ВОС = СОD= DOA = 90° => ABCD- квадрат 4.2 Ознаки квадрата А В С O D назад

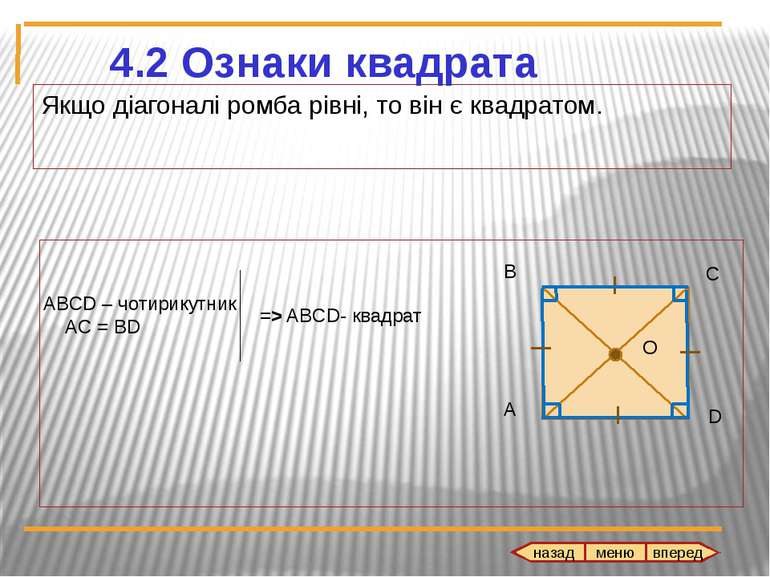
Якщо діагоналі ромба рівні, то він є квадратом. ABCD – чотирикутник AC = BD => ABCD- квадрат 4.2 Ознаки квадрата А В С O D назад

Дякую за увагу!!!

Якщо в чотирикутника всі сторони і всі кути рівні, то він є квадратом.

Якщо діагоналі прямокутника перетинаються під прямим кутом, то він є квадратом

Якщо діагоналі ромба рівні, то він є квадратом.

1. Усі кути квадрата — прямі. 2. Діагоналі квадрата перетинаються AO = OC, BO = OD і точкою перетину діляться навпіл. 3. Діагоналі квадрата рівні. АС = ВD 4. Діагоналі квадрата перетинаються AC ┴ BDпід прямим кутом. 5. Діагоналі квадрата є бісектрисами його кутів. BAO = OAD

Дякую за увагу!!!