Презентація на тему:
Об'єми тіл

Обчислення обємів геометричних тіл з допомогою визначеного інтегралу.

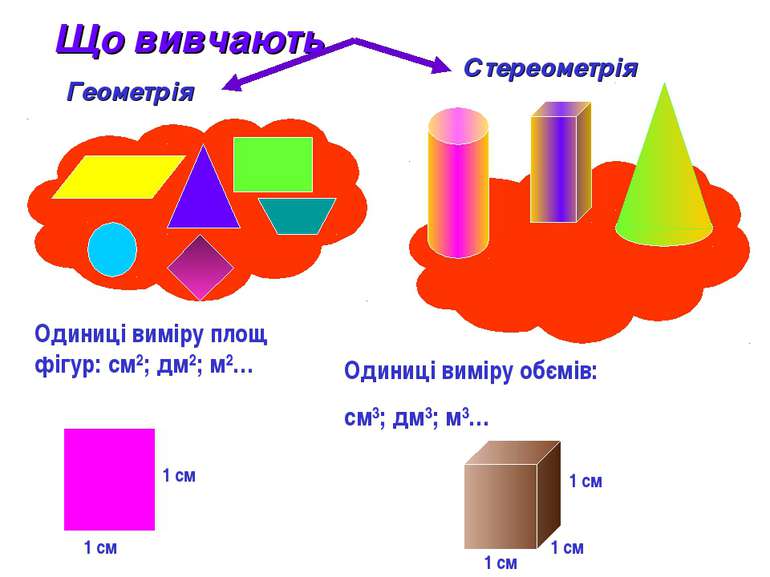
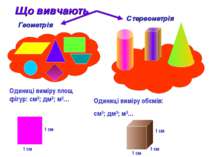
Геометрія Стереометрія Одиниці виміру площ фігур: см²; дм²; м²… 1 см 1 см Одиниці виміру обємів: см³; дм³; м³… 1 см 1 см 1 см Що вивчають

Рівні фігури мають рівні обєми

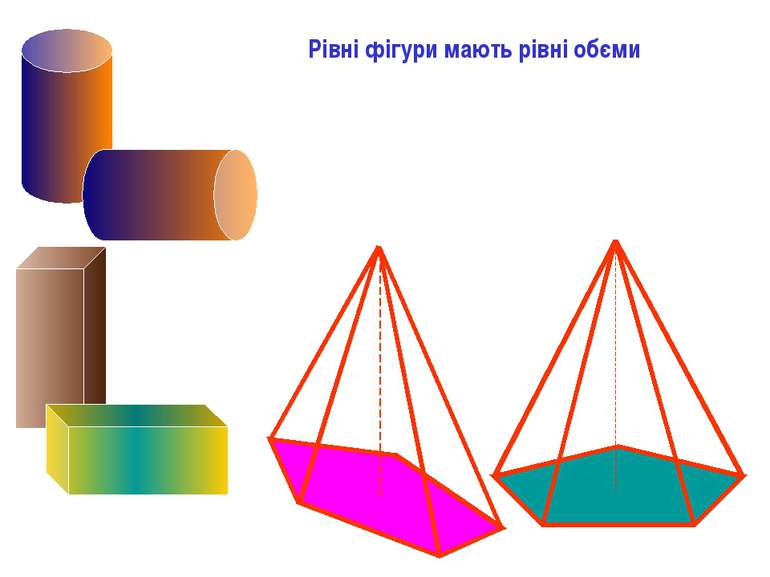
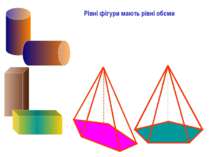
Поняття обєму в просторі вводиться аналогічно поняттю площі для фігур на площині. Визначення.  Обємом тіла називається невідємна величина, яка характеризує частину простору, зайняту тілом, і володіє слідуючими властивостями: рівні тіла мають рівні обєми; якщо тіло розбити на частини, які являються простими тілами , то обєм тіла рівний обєму його частин; за одиницю обєму прийнято обєм куба, ребро якого рівне одиниці довжини; Визначення.  Тіла з рівними обємами називаються рівновеликими. Поняття обєму.

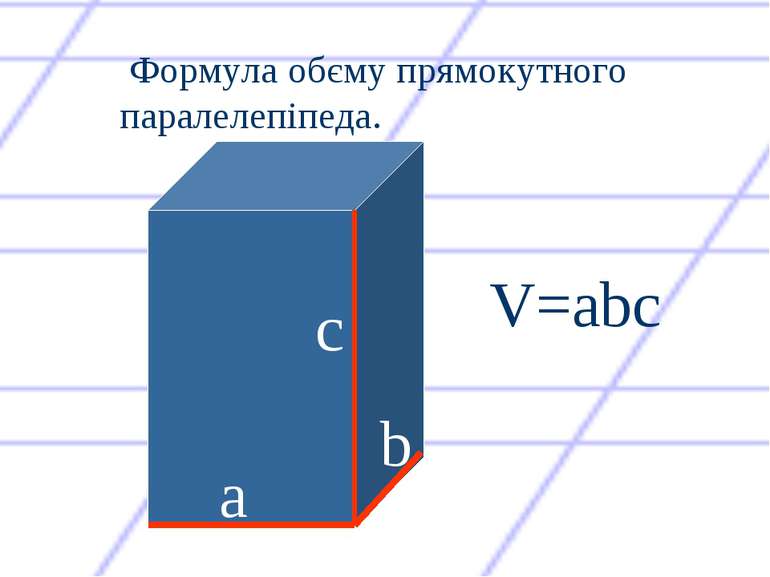
Щоб знайти обєм многогранника, потрібно розбити його на куби з ребром, рівним одиниці виміру. V=20од.3

с а b V=abc Формула обєму прямокутного паралелепіпеда.

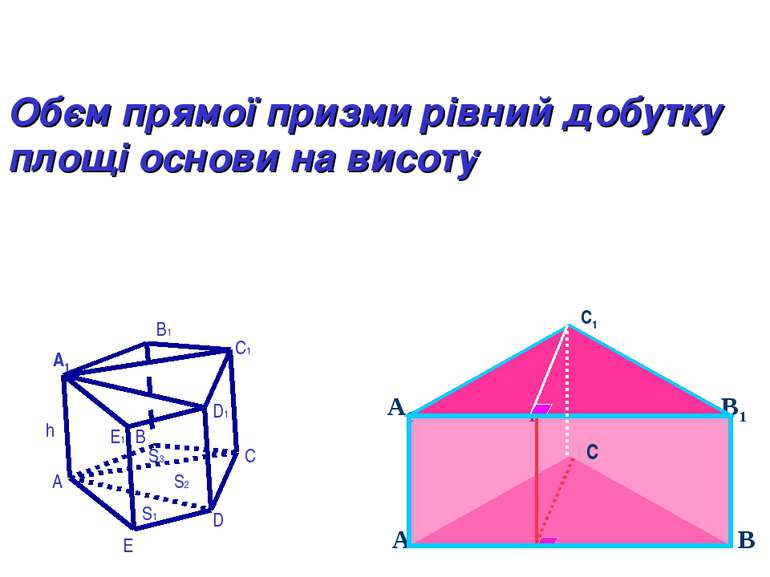
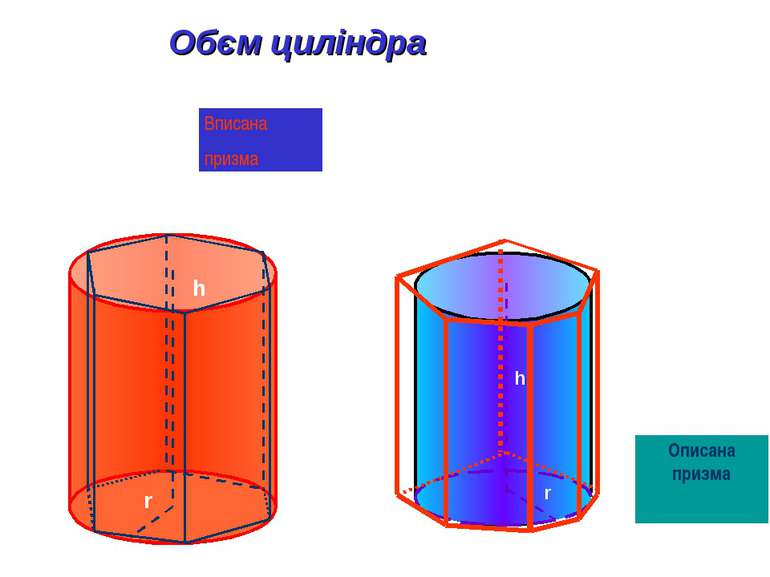
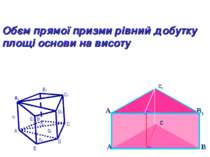
С1 Обєм прямої призми рівний добутку площі основи на висоту A E D C B h B1 C1 D1 E1 S1 S2 S3 А1 A D B A1 D1 B1 C1

Обєм циліндра h r h r Вписана призма Описана призма

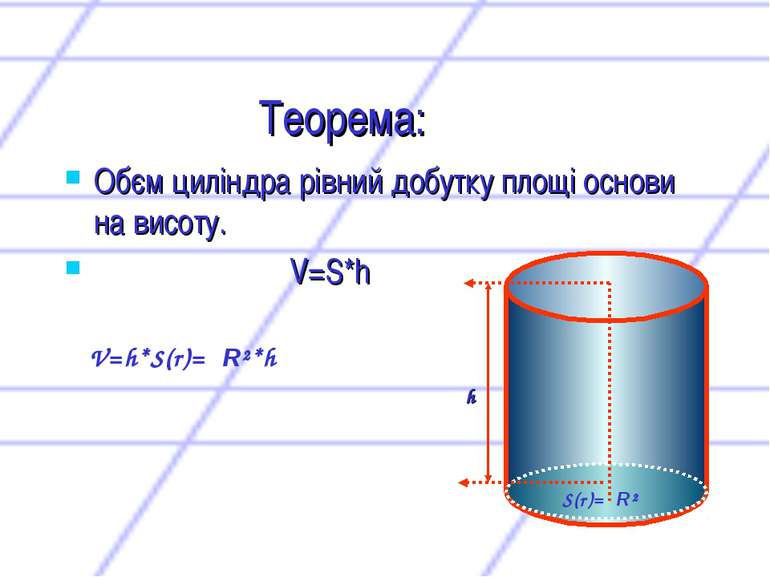
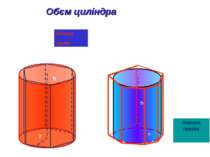
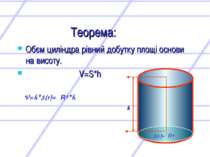
Теорема: Обєм циліндра рівний добутку площі основи на висоту. V=S*h V=h*S(r)=πR²*h S(r)=πR² h

A A1 A2 B B1 B2 C C1 C2 O X h X Обєм похилої призми Обєм похилої призми рівний добутку площі основи на висоту Трикутна призма Т.п. має S основу і висоту h. O=OX∩(АВС); OXᅩ(АВС); (АВС)||(А1В1С1) ; (А1В1С1)-площина перерізу: (А1В1С1) ᅩOX S(x)-площа перерізу; S=S(x), т.я. (АВС)||(А1В1С1) і ∆ABC=∆A1B1C1(АА1С1С-паралелограм→АС=А1С1,ВС=В1С1, АВ=А1В1)

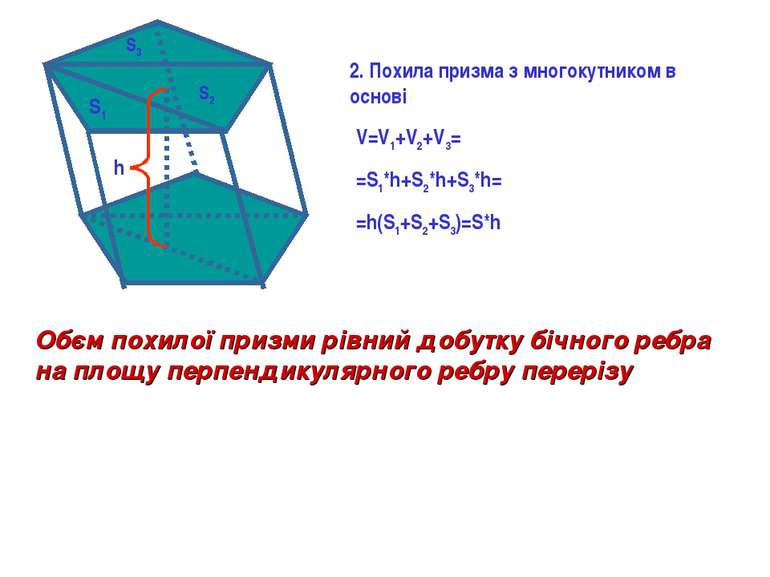
V=V1+V2+V3= =S1*h+S2*h+S3*h= =h(S1+S2+S3)=S*h S1 S2 S3 h Обєм похилої призми рівний добутку бічного ребра на площу перпендикулярного ребру перерізу 2. Похила призма з многокутником в основі

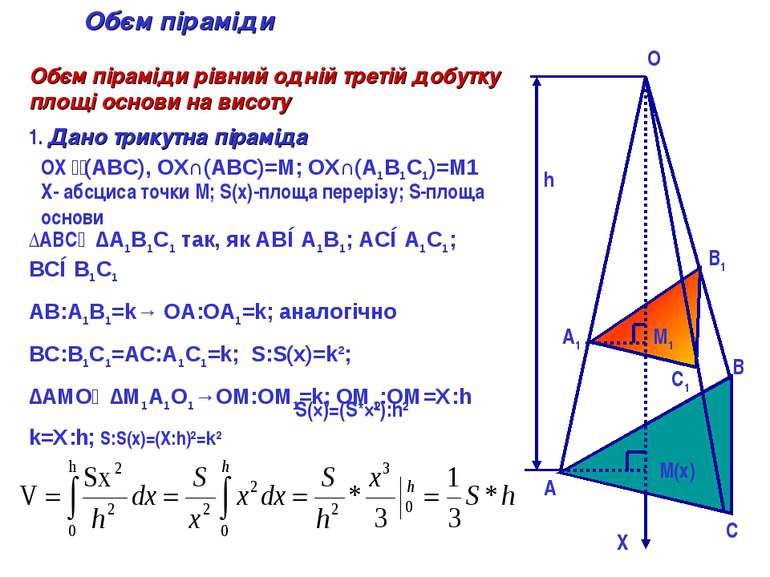
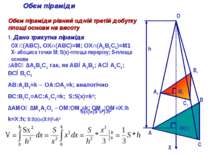
h A A1 B B1 C C1 M(х) M1 Обєм піраміди Обєм піраміди рівний одній третій добутку площі основи на висоту 1. Дано трикутна піраміда O X OXᅩ(АВС), OX∩(АВС)=М; OX∩(A1B1C1)=М1 Х- абсциса точки М; S(x)-площа перерізу; S-площа основи ∆ABC∾∆A1B1C1 так, як АВ∥А1В1; АС∥А1С1; ВС∥В1С1 АВ:А1В1=k→ ОА:ОА1=k; аналогічно ВС:В1С1=АС:А1С1=k; S:S(x)=k²; ∆AMO∾∆M1A1O1→OM:OM1=k; ОМ1:ОМ=Х:h k=Х:h; S:S(x)=(Х:h)²=k² S(×)=(S*ײ):h²

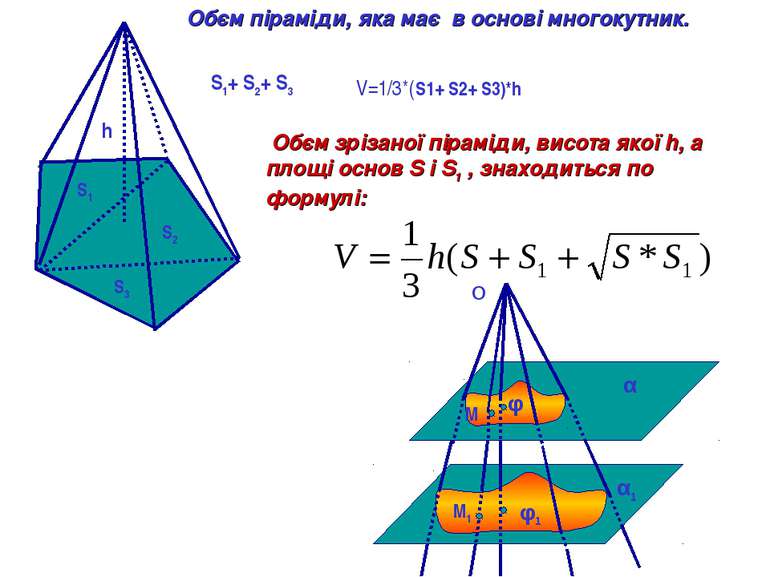
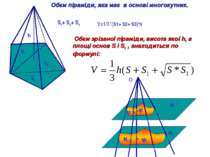
S1+ S2+ S3 S1 S2 S3 h V=1/3*(S1+ S2+ S3)*h Обєм піраміди, яка має в основі многокутник. Обєм зрізаної піраміди, висота якої h, а площі основ S і S1 , знаходиться по формулі: α α1 φ φ1 М М1 O

Обєм конуса рівний одній третій добутку площі основи на висоту. h х х O A A1 М М1 R R1

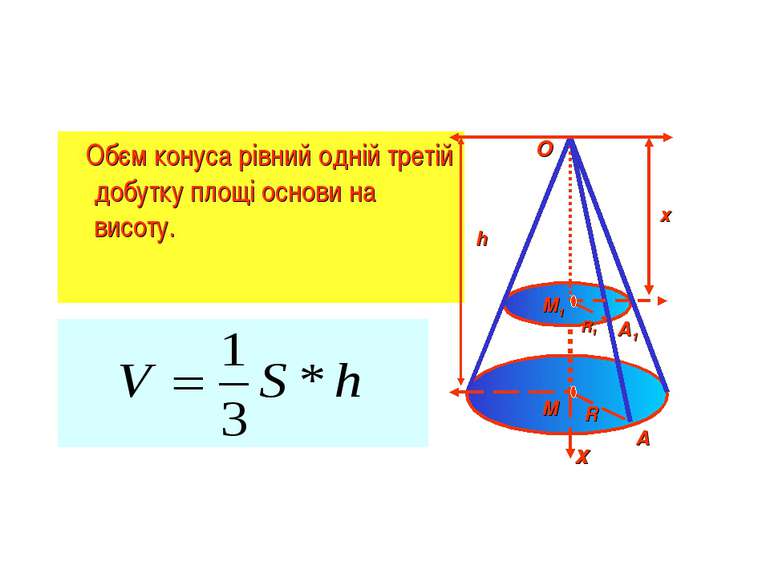
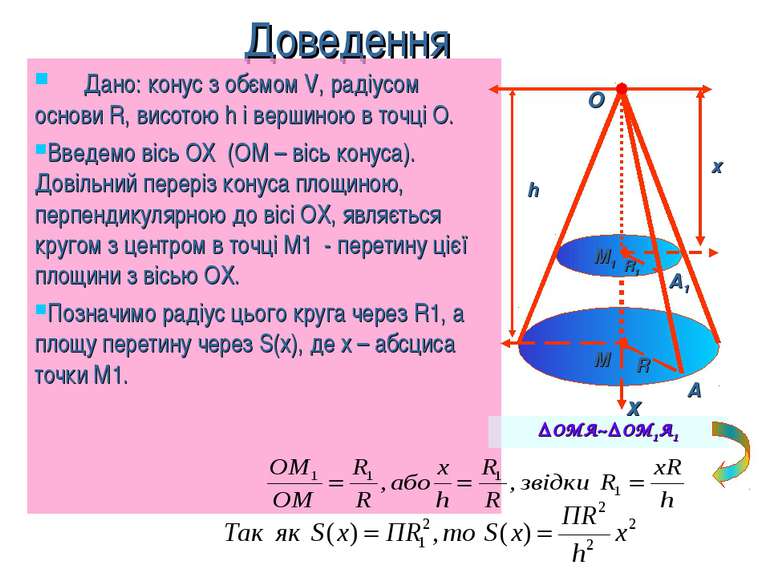
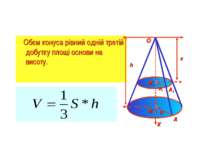
Доведення Дано: конус з обємом V, радіусом основи R, висотою h і вершиною в точці О. Введемо вісь ОХ (ОМ – вісь конуса). Довільний переріз конуса площиною, перпендикулярною до вісі ОХ, являється кругом з центром в точці М1 - перетину цієї площини з вісью ОХ. Позначимо радіус цього круга через R1, а площу перетину через S(х), де х – абсциса точки М1. h х х A A1 М М1 R R1 O ΔОМА~ΔОМ1А1

Використовуючи основну формулу для обчислення обємів тіл при а=0, b=h, одержуємо h х х A A1 М М1 R R1 O Площа S основи конуса рівна ПR², тому Обєм V зрізаного конуса, висота якого рівна h, а площі основ рівні S і S1, знаходиться по формулі

A М O C ⍶ х х Обєм кулі Теорема :Обєм кулі радіуса R рівний 4/3πR³ Дано: куля, Rш ; О- центр кулі; ОХ – вісь кулі; αᅩOX ;М- центр круга перерізу; ОС=r; Sпер. = S (x); х- абсциса М Знайти : V S (x)=πr² S (x)=π(R²-x²) -R≤ x ≤R Використовуючи основну формулу для обчислення обємів маємо :а =-R; b=R r R

A B O C ⍶ АВ=h х Кульовим сегментом називається частина кулі ,яка відтинається від неї площиною. На рисунку два кульові сегменти- верхній і нижній. Круг , одержаний в перерізі – основа сегмента, АВ- висота верхнього сегмента, ВС- висота нижнього сегмента (обидва відрізки –частини діаметра АС. ОК=Rк.) К Vк. с .=πh²(R-1/3h) OX ￌ ⍶ S (x)=πх², де R-h ≤x ≤R де S (x)- площа перерізу V=π∫(R²-x²)dx=π(R²x-x³/3)| =πh²(R-1/3h) R R-h R-h R По правилу обчислення обємів a=R-h; b=R S (x)- неперервна функція на [a; b] h

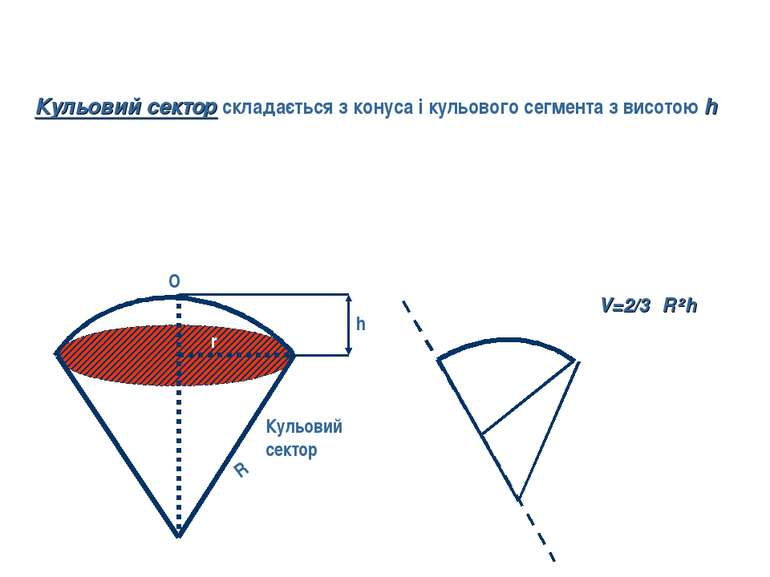
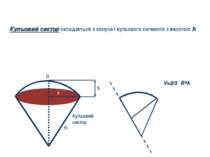
h R r O Кульовий сектор V=2/3πR²h Кульовий сектор складається з конуса і кульового сегмента з висотою h