Презентація на тему:
ЕЛЕМЕНТИ ТЕОРІЇ ЙМОВІРНОСТЕЙ

ЕЛЕМЕНТИ ТЕОРІЇ ЙМОВІРНОСТЕЙ

Місце теми в шкільному курсі математики Алгебра, 9 клас (12-річна школа)

Алгебра і початки аналізу, 11 клас (11-річна школа)

Алгебра і початки аналізу, 11 клас (12-річна школа)

Алгебра, 9 клас, поглиблене вивчення (12-річна школа)

Алгебра і початки аналізу, 11 клас, поглиблене вивчення

Основні поняття теорії ймовірностей Стохастичний експеримент - експеримент, точний результат (наслідок) якого передбачити неможливо. Випробування - кожне конкретне (окреме) проведення стохастичного експерименту. Елементарна подія - кожний можливий наслідок стохастичного експерименту. Простір елементарних подій - множина всіх можливих наслідків стохастичного експерименту.

Основні поняття теорії ймовірностей Приклади. 1. Підкидання монети один раз і фіксація грані, якою монета впаде догори. Множина всіх можливих наслідків складається з двох наслідків: «монета падає догори гербом» і «монета падає догори цифрою». Це можна записати так : г, ц . 2. Підкидання грального кубика один раз і фіксація кількості очок на грані, що випала догори. 1, 2, 3, 4, 5, 6 . 3. Підкидання двох гральних кубиків один раз і фіксація суми очок на гранях, які випали догори. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 .

Основні поняття теорії ймовірностей Приклади. 4. Фіксація номера кульки, яка викочується з лототрону в таких іграх, як лото «Забава», «Укрлото», «Спортлото» тощо. Множина містить усі числа, які відповідають номерам кульок. Оскільки в лото «Забава» в лототроні 75 кульок, то 1, 2, 3, …, 75 . 5. Вибір навмання числа з відрізка [ a; b ], де a та b дійсні числа і його фіксація. [ a; b ] . Запропонуйте свої приклади стохастичних експериментів та вкажіть відповідні їм простори елементарних подій

Поняття випадкової події Випадковими подіями (або просто подіями) називають деякі з підмножин простору елементарних подій . !!! Кожна випадкова подія є деякою сукупністю певних наслідків експерименту, тобто підмножиною простору . Проте не кожна підмножина простору є подією !!! Порожня множина і сама множина завжди вважаються подіями.

Поняття випадкової події Події позначають великими латинськими буквами А, В, С тощо. Оскільки кожна подія є деякою множиною, то її можна задати переліком її елементів – елементарних подій, або словесно – описанням характеристичної властивості її елементів. Кожну елементарну подію е, з яких складається подія А, називають елементарною подією, що сприяє події А і позначають е А. Усі інші елементарні події е вважаються такими, що не сприяють події А і позначають е А. Наприклад, в експерименті з підкиданням грального кубика події А 2, 4, 6 («випала парна кількість очок») сприяє три елементарних події: 2, 4 і 6, а 1, 3 і 5 не сприяють події А. Події В = («випало не більше, ніж 6 очок») сприяють всі шість елементарних подій: 1, 2, 3, 4, 5, 6. Події С = («випало більше, ніж 6 очок») не сприяє жодна елементарна подія з простору .

Поняття випадкової події Якщо в результаті випробування відбулася елементарна подія е, що сприяє події А (е А), то кажуть, що в результаті цього випробування подія А відбулася; якщо в результаті випробування не відбулася жодна елементарна подія е А, то кажуть, що в результаті цього випробування подія А не відбулася. Простір елементарних подій є початковою математичною моделлю стохастичного експерименту. Геометрично простір елементарних подій зображають у вигляді прямокутника, а події – частинами цього прямокутника, наприклад кругами.

Вірогідна та неможлива події Подія – множина усіх можливих наслідків експерименту. В результаті кожного випробування подія обов’язково відбудеться. Тому подію називають вірогідною (або достовірною). Інакше, вірогідною є подія, яка відбувається в результаті кожного випробування, пов’язаного з даним стохастичним експериментом. Подія не містить жодної елементарної події е з множини , тому вона ніколи не може відбутися в результаті проведення експерименту. Подію називають неможливою. Інакше кажучи, неможливою є подія, яка не може відбутися в результаті будь-якого випробування, пов’язаного з даним стохастичним експериментом.

Рівні події Якщо подія В відбувається завжди, коли відбувається подія А, то пишуть і кажуть, подія В спричинюється подією А або подія А спричинює подію В. Це означає, що кожна елементарна подія е, що сприяє події А (е А), сприяє також і події В (е В). Якщо подія А спричинює подію В і подія В спричинює подію А ( і В А), то події А і В називають рівними, або рівносильними, або еквівалентними і записують А = В. Це означає, що кожна елементарна подія, що сприяє події А, сприяє також і події В, та навпаки, кожна елементарна подія, що сприяє події В, сприяє також і події А. Інакше, події А і В рівні тоді і тільки тоді, коли вони одночасно відбуваються або не відбуваються.

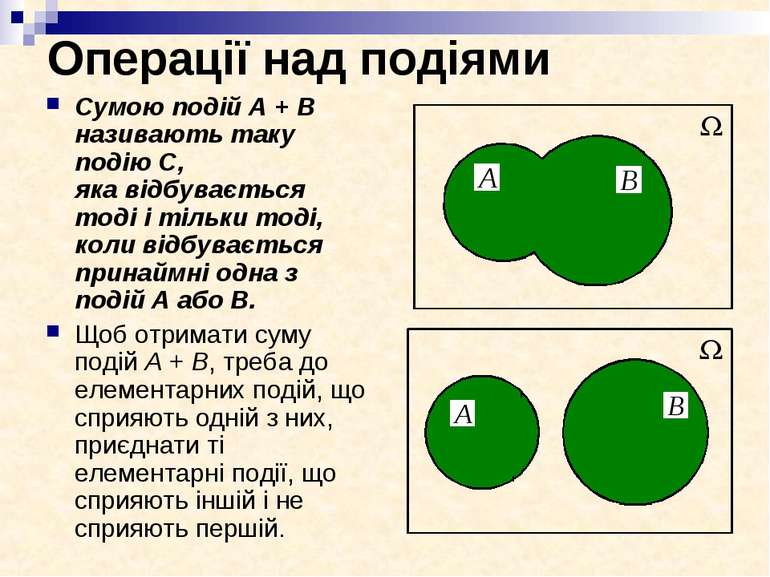
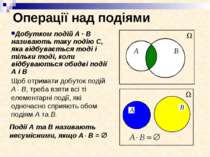
Операції над подіями Сумою подій А + В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбувається принаймні одна з подій А або В. Щоб отримати суму подій А + В, треба до елементарних подій, що сприяють одній з них, приєднати ті елементарні події, що сприяють іншій і не сприяють першій.

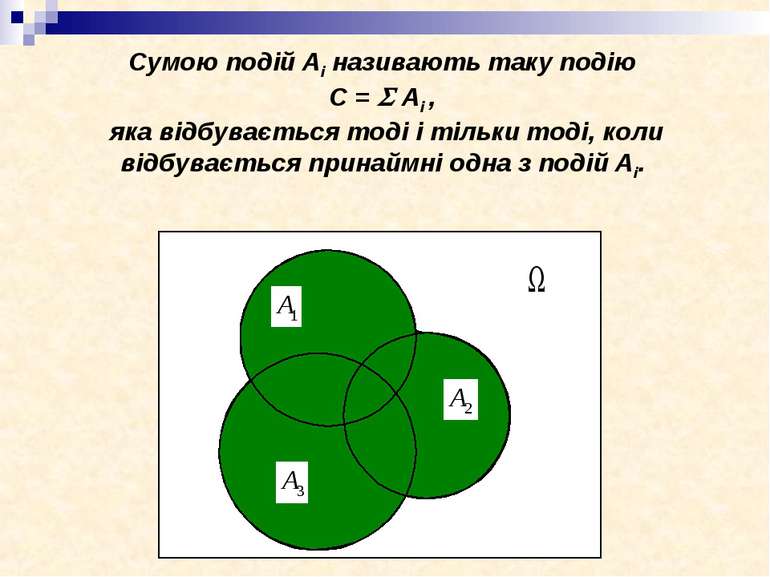
Сумою подій Аі називають таку подію C = Ai , яка відбувається тоді і тільки тоді, коли відбувається принаймні одна з подій Аі.

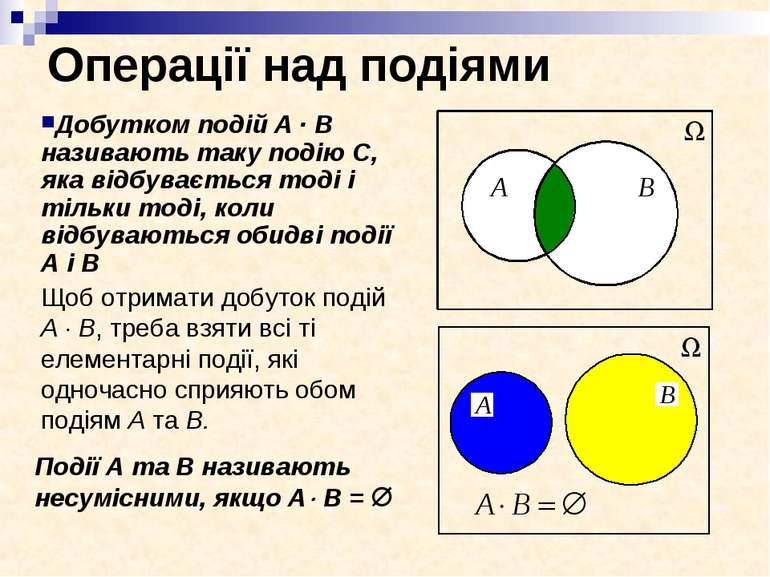
Операції над подіями Щоб отримати добуток подій А В, треба взяти всі ті елементарні події, які одночасно сприяють обом подіям А та В. Події А та В називають несумісними, якщо А В = Добутком подій А · В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбуваються обидві події А і В

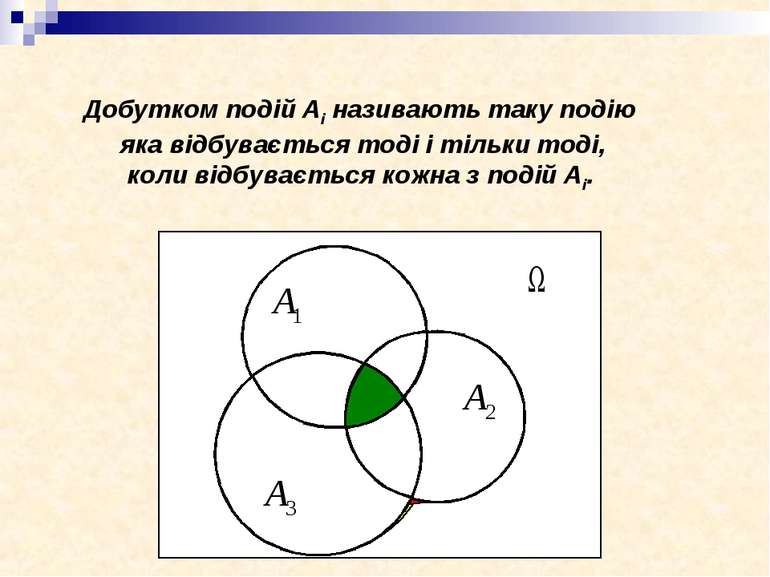
Добутком подій Аі називають таку подію яка відбувається тоді і тільки тоді, коли відбувається кожна з подій Аі.

Операції над подіями Різницю А називають подією, протилежною до події А і позначають Ā Різницею А В подій А та В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбувається подія А і не відбувається подія В.

Означення випадкової події Випадковими подіями або просто подіями називають такі підмножини простору Ω, які утворюють деяку сукупність S, що задовольняє три основні умови: 1s. S - вірогідна подія завжди належить цій сукупності; 2s. Якщо А S, то Ā S - кожна подія належить цій сукупності разом зі своєю протилежною подією; 3s. Якщо Аi S, i N, то Аi S - для будь-яких подій, що належать даній сукупності, їх сума також належить цій сукупності. Таку сукупність S називають простором подій. Кожну підмножину , що входить до S, вважають подією, а всі інші підмножини Ω не вважають подіями.

Простір випадкових подій Простір подій S можна утворювати багатьма способами. Головним при побудові простору подій є виконання основних властивостей подій 1s – 3s, які можна назвати правилами побудови простору подій або правилами визначення випадкових подій. Наприклад, при підкиданні грального кубика простір елементарних подій 1, 2, 3, 4, 5, 6 . Нам важливо, щоб подією було випадання парної кількості очок. Тоді в S повинні входити Ω, , А = {2, 4, 6} (за умовою завдання) і Ā= {1, 3, 5} (за властивістю 2s). Cукупність , , 1, 3, 5 , 2, 4, 6 можна вважати простором випадкових подій S і при цьому кожен елемент цієї сукупності є випадковою подією. Усі інші підмножини при цьому не вважаються подіями.

Простір випадкових подій Множину , , 1, 3, 5 , 1, 2 не можна вважати простором випадкових подій, оскільки не виконуються умови 2 і 3. Приєднуючи до неї підмножини 2, 4, 6 , 3, 4, 5, 6 , 1, 2, 3, 5 , 4, 6 , 1, 2, 4, 6 , 3, 5 , отримаємо сукупність, яка буде задовольняти умови 1s – 3s і яку можна назвати простором подій. Сукупність S*, утворена з усіх підмножин простору , також задовольняє умови 1s – 3s. Вона називається найширшим простором подій, а сукупність S* = {Ω, } називається найвужчим простором подій (пов’язаних з даним простором ) Простір S разом з простором елементарних подій дає уточнену модель даного випадкового експерименту.

Статистична ймовірність події Нехай дано експеримент і визначено простір елементарних подій та простір подій S. Для цього експерименту проведено n випробувань і при цьому фіксована елементарна подія е відбулася m раз, 0 ≤ т ≤ n. Число m випробувань, у яких відбулася елементарна подія е називається її абсолютною частотою, а відношення m до n називається відносною частотою елементарної події е в даній серії з n випробувань. Відносна частота елементарної події е характеризує середню можливість її відбування у кожному з n випробувань. Позначається і обчислюється за формулою

Статистична ймовірність події Нехай дано експеримент і визначено простір елементарних подій та простір подій S. Для цього експерименту проведено n випробувань і при цьому фіксована елементарна подія A S відбулася m раз, 0 ≤ т ≤ n. Означення. Число т випробувань, у яких відбулася подія А називається її абсолютною частотою, а відношення m до n називається відносною частотою або статистичною ймовірністю події А в даній серії із n випробувань. Статистична ймовірність події А характеризує середню можливість її відбування у кожному з n випробувань. Позначається і обчислюється за формулою

Статистична ймовірність події Наприклад. Нехай проведено n = 20 підкидань кубика, на гранях якого нанесені числа 1, 2, 3 і зафіксовано такі випадання чисел: 1, 3, 2, 2, 1, 1, 1, 3, 3, 2, 3, 1, 2, 2, 3, 1, 3, 2, 1, 2. Побудуємо простір подій S = , , . Події А = , сприяють елементарні події е1 = 1 і е3 = 3, які спостерігалися 7 і 6 разів відповідно. Отже, m1 = 7 і m3 = 6 абсолютні частоти цих елементарних подій в даній серії випробувань, а абсолютна частота події А є m = 13. Відносні частоти будуть відповідно дорівнювати:

Основні властивості статистичної ймовірності

Властивості статистичної ймовірності

Властивості статистичної ймовірності