Презентація на тему:
Теория нормализации

Лекция 8. Теория нормализации отношений реляционной модели Национальный авиационный университет Факультет компьютерных наук Кафедра инженерии программного обеспечения

СОДЕРЖАНИЕ В чем суть теории нормализации РМ Плохие проекты БД Функциональные зависимости Многозначные зависимости Зависимости по соединению Нормальные формы Проектирование схемы реляционной модели данных

В чем суть теории нормализации Теория нормализации схем отношений реляционной модели данных – это теория, устанавливающая: каким образом исходная схема отношений может быть преобразована в другую результирующую схему, которая эквивалентна в некотором смысле исходной и в каком-то смысле лучше ее. Таким образом эта теория должна ответить на следующие вопросы: какие существуют критерии эквивалентности схем отношений; какие существуют критерии оценки качества схем отношений; какие существуют механизмы эквивалентных преобразо- ваний схем отношений, дающие более качественные схемы.

Плохие проекты БД (1)

Плохие проекты БД (2)

Нормализация

Сложные домены и первая нормальная форма (1NF)

Функциональная зависимость

Ключи

Свойства функциональных зависимостей

Логические следствия зависимостей

Замыкание, полнота, эквивалентность и минимальное покрытие FD

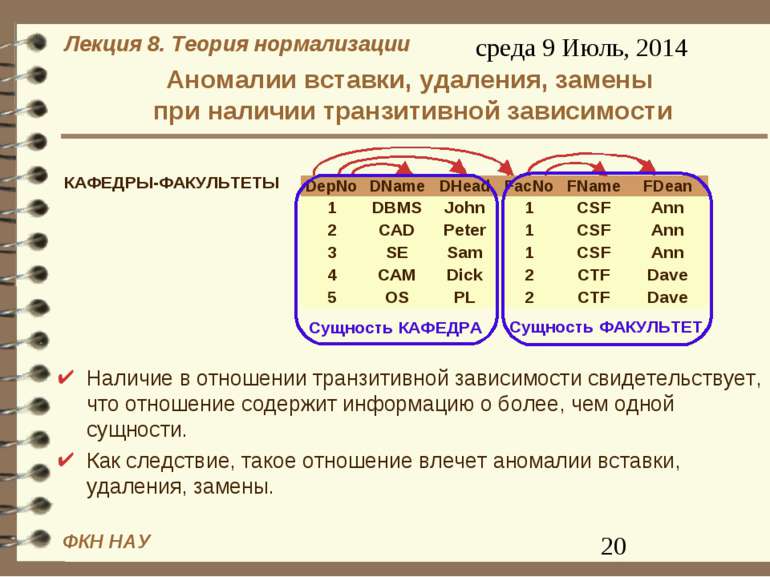
FD и сущности предметной области Тезис. Если в ПО существует FD А В, то в этой ПО имеется класс сущностей, определенных на атрибутах (А,В) , причем А является ключом сущностей этого класса, а В – обычный их атрибут. Если А В1, А В2, …, А Вn, то существует класс сущностей с атрибутами (А, В1,…,Вn), где А – ключ, а В1,…, Вn – обычные атрибуты.

Неполная (частичная) функциональная зависимость и вторая нормальная форма (2NF)

Аномалии вставки, удаления, замены при наличии неполной FD

Вторая нормальная форма (2NF)

Пример приведения в 2NF

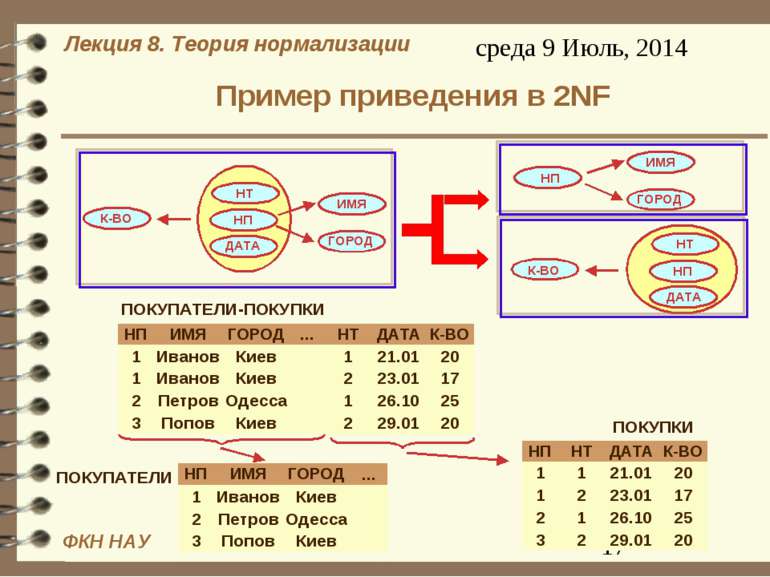
Пример приведения в 2NF - итоги Исходное отношение содержит информацию о двух сущностях, результирующие – каждое по одной сущности. Результирующие отношения не содержат аномалий вставки, удаления, замены. Исходное отношение можно восстановить из результирующих с помощью операции естественного соединения. При таком разбиении не теряются функциональные зависимости (то есть зависимости исходного и результирующих отношений эквивалентны)

Транзитивная зависимость и 3NF

Аномалии вставки, удаления, замены при наличии транзитивной зависимости

Третья нормальная форма (3NF)

Пример приведения в 3NF

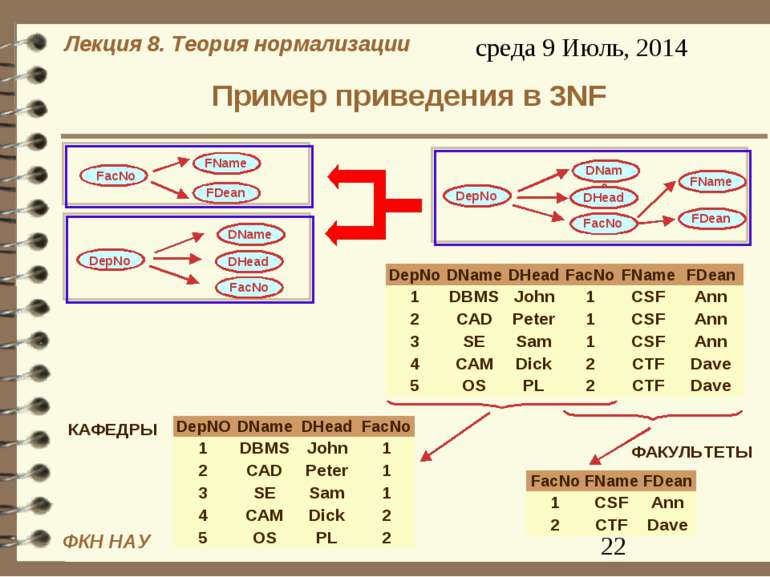
Пример приведения в 3NF - итоги Результаты те же, что и при приведении в 2NF: Исходное отношение содержит информацию о двух сущностях, результирующие – каждое по одной сущности. Результирующие отношения не содержат аномалий вставки, удаления, замены. Исходное отношение можно восстановить из результирующих с помощью операции естественного соединения. При таком разбиении не теряются функциональные зависимости (то есть зависимости исходного и результирующих отношений эквивалентны)

Усиленная 3NF (S3NF)

Приведение в S3NF

Нормальная форма Бойса-Кодда (BCNF)

Многозначная зависимость и 4NF

Определение многозначной зависимости (MVD)

Аксиомы MVD

Аксиомы связи FD и MVD 1) Аксиома репликации

Дополнительные свойства MVD 1) Объединение

Четвертая нормальная форма (4NF)

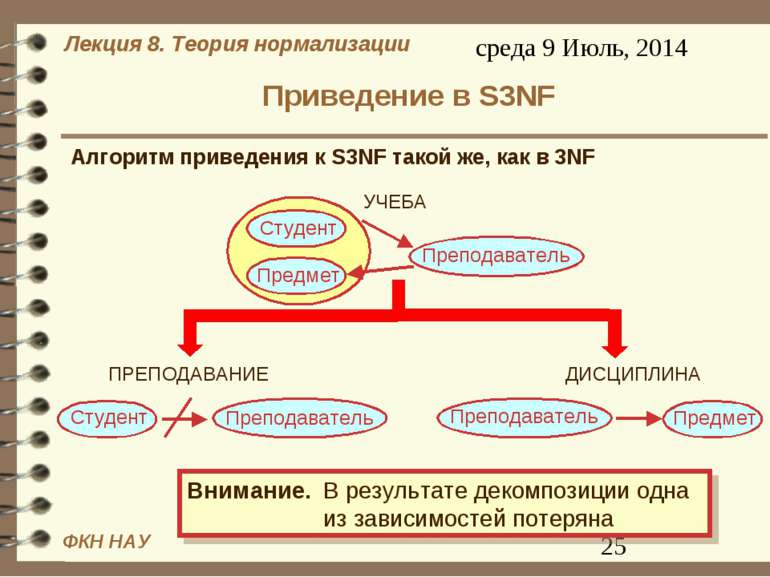
Приведение в 4NF и встроенные MVD Алгоритм приведения к 4NF. Пусть задано отношение R с атрибутами А, В, С, и имеется многозначная зависимость R.A R.B Тогда отношение R декомпозируются на следующие два отношения: R[A, B] и R[B, С]. Если результирующие отношения все еще не находятся в 4NF, то к ним опять применяется этот алгоритм.

Зависимость по соединению (JD) и пятая нормальная форма

Связь зависимостей по соединению (JD) и многозначных зависимостей (MVD) Каждая JD вида *(A, B) в отношении со схемой R(A,B), где А и В - множества атрибутов, является эквивалентной MVD А ∩ В →→ А и А ∩ В →→ В. (Любая MVD является JD, но не наоборот!!!) Однако, существуют JD, которые не эквивалентны никакой MVD. Так, например, если в отношении R = (A, B, C) имеется JD *((A,B), (B, C), (A,C)), то она не эквивалентна никакой MVD. Пример:

Пятая нормальная форма - 5NF Введение 5NF аргументируется тем, что никакая n-арная декомпозиция отношения не может быть представлена в виде последовательности бинарных декомпозиций.

Пример отношения в 5NF

Пример отношения, нарушающего 5NF, и приведения в 5NF

Пример отношения, нарушающего 4NF, и приведения в 4NF

Проектирование схемы реляционной модели данных Формальная постановка задачи проектирования реляционной схемы Декомпозиция схемы реляционного отношения Эквивалентность отношений Декомпозиция без потери (с сохранением) данных Декомпозиция без потери (с сохранением) зависимостей Эквивалентность нормальных форм Критерий качества реляционной схемы

Формальная постановка задачи проектирования реляционной схемы В этом определении следует уточнить: процедуру представления отношений в виде совокупности других; понятие эквивалентности схем отношений; критерий качества схемы отношений.

Декомпозиция схемы реляционного отношения Декомпозицией отношения R со схемой R(M) называется процедура разбиения R на множество отношений R1, R2,…, Rn со схемами R1(M1),…, Rn(Mn), которая удовлетворяет следующим требованиям: М1 М2 … Мn = М. Другими словами, любой атрибут из R должен содержаться в по крайней мере одном из отношений Ri и все Ri должны быть определены на атрибутах R. Все отношения Ri (1 i n), являются проекциями исходного отношения R по атрибутам, содержащимся в Ri, то есть Ri(Mi) = Mi(R)

Эквивалентность схем отношений по зависимостям

Эквивалентность отношений по данным

Эквивалентность нормальных форм

Критерий качества реляционной схемы Рассмотрим теперь вопрос, что значит одна схема отношений лучше другой. Здесь можно говорить о критериях независимости представ- ления связей и степени неизбыточности данных и, как след- ствие, об отсутствии возможных аномалий манипулирования данными. Фактически эти качества можно оценить характеристиками нормальных форм отношений. Чем в более высокой" нормальной форме находится совокупность отношений, тем более независимо представлены в них функциональные и многозначные зависимости.