Презентація на тему:
Імовірнiсть події

Тема 5 Елементи прикладної математики Математичне моделювання Відсоткові розрахунки. Поняття про теорію імовірностей. Основні поняття теорії імовірностей. Ймовірність випадкової події Початкові відомості про математичну статистику. Статистичні дані. Способи подання даних Середнє значення. Розв'язування вправ

Пункт 8.3 Поняття імовірності події. Внаслідок випробування (виймання кулі з урни) одна з цих подій настає з необхідністю, тобто вони утворюють повну групу. Крім цього, ці події будуть попарно несумісними, бо коли, наприклад, відбувається подія А2, то інша подія при випробуванні не настає. Події Aі будуть і рівноможливими, бо немає підстав твердити, що, наприклад, подія А3 більш можлива, ніж подія А8. Таким чином, події A1 , A2 , А3 , А4 , А5 , А6 , А7 , А8 , А9. становлять сукупність попарно несумісних і рівноможливих подій, які утворюють повну групу. Події, що становлять такі сукупності, називають елементарними (або випадками). Імовірність випадкової події Елементарна подія, при якій настає подія А, називається сприятливою для цієї події.

Запитання для самоперевірки Що називається імовірністю події? В яких межах перебуває імовірність будь-якої події? Яка імовірність того, що навмання взята кулька з коробки виявиться червоною?

Пункт 8.3 Поняття імовірності події. Одним із найважливіших понять теорії імовірностей є поняття імовірності події. Приклад. В урні лежать 9 однакових за розміром і різних за кольором куль (4 синіх, 3 жовтих і 2 зелених). При такому розподілі куль за кольорами можна стверджувати, що при вийманні з урн однієї кулі можливість узяти синю кулю є більшою, ніж можливість узяти зелену. Виявляється, що кожній з таких можливостей можна дати числову характеристику. Для цього умовно пронумеруємо кулі: сині кулі позначимо номерами 1, 2, 3, 4, жовті — 5, 6, 7, зелені — 8, 9. Якщо через А (і = 1, 2, 3, 4,..., 9) позначимо подію «з'явилася куля з номером і», то можемо розглянути такі події: A1 , A2 , А3 , А4 , А5 , А6 , А7 , А8 , А9. Імовірність випадкової події Елементарна подія, при якій настає подія А, називається сприятливою для цієї події.

Пункт 8.3 Поняття імовірності події. При елементарних подіях A1 або А2, або А3, або А4 настає подія «з'явилася синя куля». При інших елементарних подіях ця подія не настане. Отже, елементарні події A1 , A2 , А3 , А4 сприяють появі кульки синього кольору, а елементарні події А5 , А6 , А7 , А8 , А9 віднести до несприятливих для цієї події. Імовірність події А позначають так: Р(А). Отже, , де m — кількість елементарних подій, які сприяють події А, n — загальна кількість попарно несумісних і рівноможливих подій, які утворюють повну групу. Імовірність випадкової події Імовірністю події А називають відношення кількості випадків, які сприяють події А, до кількості всіх можливих випадків.

Поняття імовірності події Позначимо ці події відповідно через А, В, С. З усіх дев'яти елементарних подій події А сприяють 4, події В — З, події С — 2 елементарні події. Відтак: Зрозуміло, що імовірність вірогідної події дорівнює 1, бо такій події сприяють усі можливі випадки (т = n). Якщо, наприклад, в урні містяться 4 сині кульки, то в такому випадку імовірність виймання синьої кульки становить Обчислимо імовірність виймання синьої, жовтої і зеленої кульок. Iмовірність вірогідної події дорівнює 1

Поняття імовірності події Імовірність неможливої події дорівнює нулю, бо неможливій події не сприяє жоден із можливих випадків (т =0). Якщо, наприклад, в урні міститься 4 синіх і 3 жовтих кульки, то імовірність витягування білої кульки (подія D) становить Імовірність неможливої події дорівнює нулю Імовірність випадкової події А задовольняє подвійну нерівність 0

Обчислення імовірності подій Приклад 1. Кожна пластинка доміно поділена лінією на дві частини, на яких вирізьблені вічка від 0 до 6. Знайдіть імовірність того, що на взятій навмання пластинці з комплекту доміно (хоча б на одній з її частин) буде 6 вічок. Розв'язання. Кількість усіх пластинок доміно можна обчислити, скориставшись такою таблицею, де записано можливі кількості вічок на кожній частині пластинки: 00 01 02 03 04 05 06 11 12 13 14 15 16 22 23 24 25 26 33 34 35 36 44 45 46 55 56 66 Простий підрахунок показує, що кількість можливих випадків діставання пластинок (кількість усіх пластинок доміно) дорівнює 28. Кількість випадків, що сприяють настанню події А, дорівнює 7 (кількість пластинок, на яких є 6 очок — принаймні на одній з половин пластинки).

Пункт 8.2 Приклад 2. Набираючи номер телефону, абонент забув одну з цифр і набрав її навмання. Знайдіть імовірність того, що була набрана потрібна цифра. Розв'язання. Абонент може набрати одну з таких цифр: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9. Число можливих випадків дорівнює 10. Лише один з випадків сприяє нашій події (набрати потрібну цифру). Отже, імовірність події А становить: Обчистення імовірності події

Первинне закріплення вивченого матеріалу 391. Знайдіть імовірність того, що при одному киданні грального кубика випаде парне число. При киданні грального кубика може випасти 1, 2, 3, 4, 5 або 6 очок. Шуканій події сприяють випадки: випаде 2 очка, випаде 4 очка, випаде 6 очок. Тобто n=6, m=3. Отже,

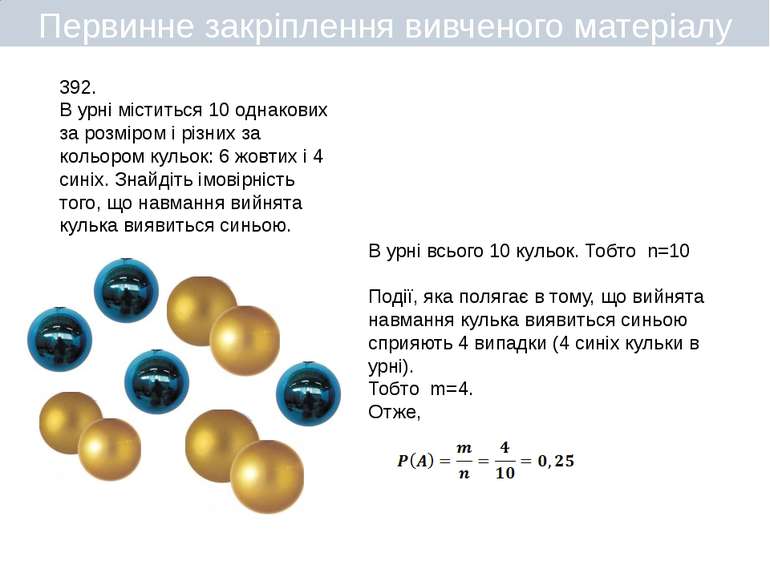
Первинне закріплення вивченого матеріалу 392. В урні міститься 10 однакових за розміром і різних за кольором кульок: 6 жовтих і 4 синіх. Знайдіть імовірність того, що навмання вийнята кулька виявиться синьою. В урні всього 10 кульок. Тобто n=10 Події, яка полягає в тому, що вийнята навмання кулька виявиться синьою сприяють 4 випадки (4 синіх кульки в урні). Тобто m=4. Отже,