Презентація на тему:
Рекурсія
Завантажити презентацію
Рекурсія
Завантажити презентаціюПрезентація по слайдам:
Програми можуть містити виклик однієї або декількох підпрограм. Підпрограми можуть, в свою чергу, викликати інші підпрограми. А чи може підпрограма викликати саму себе?
Алгоритмічна конструкція, в якій підпрограма викликає сама себе, називається рекурсією. Рекурсивні алгоритми зазвичай виникають там, де вихідну задачу можна звести до такої ж самої, але з іншими аргументами або в інших обставинах.
В житті ми маємо такі випадки, коли будь-яке поняття визначається з використанням того ж самого поняття (рекурсія): цукерка "Ану-ка отними" має на фантику зображення цукерки, яка має зображення цукерки і так далі; всім відома російська приказка "У попа была собака…"; луна в горах.
Рекурсія дає змогу записувати циклічні алгоритми без використання команд циклу. Розглянемо приклади запису рекурсивних алгоритмів.
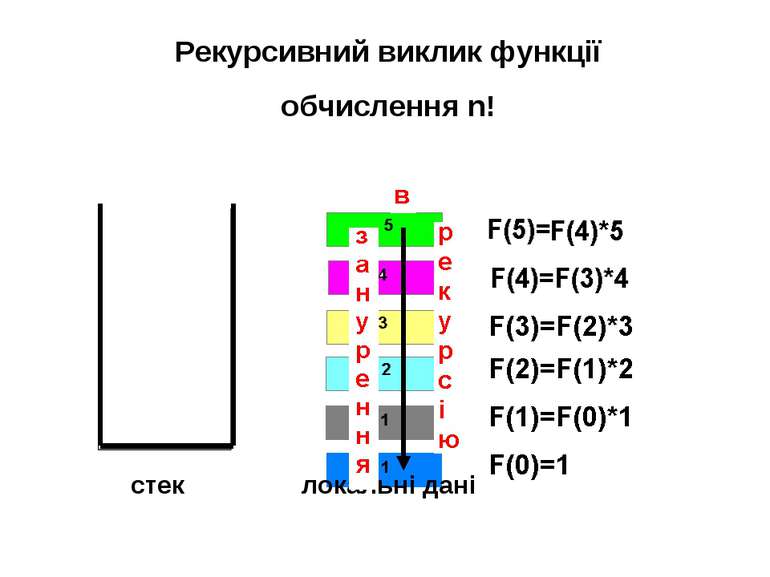
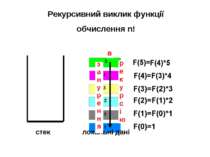
Обчислення факторіалу числа: n!=1*2*3*…*n 1)Звичайний спосіб: Fact:=1; for i:=1 to n do Fact=Fact * і ; 2) Рекурсивний спосіб: n!= 1, при n=0 (0!=1,1!=1 за визначенням) ; (n-1)!* n , при n>0. Текст функції: Function Fact( n : integer) : integer; begin If n=0 then Fact:=1 else Fact:= Fact(n-1) * n end;
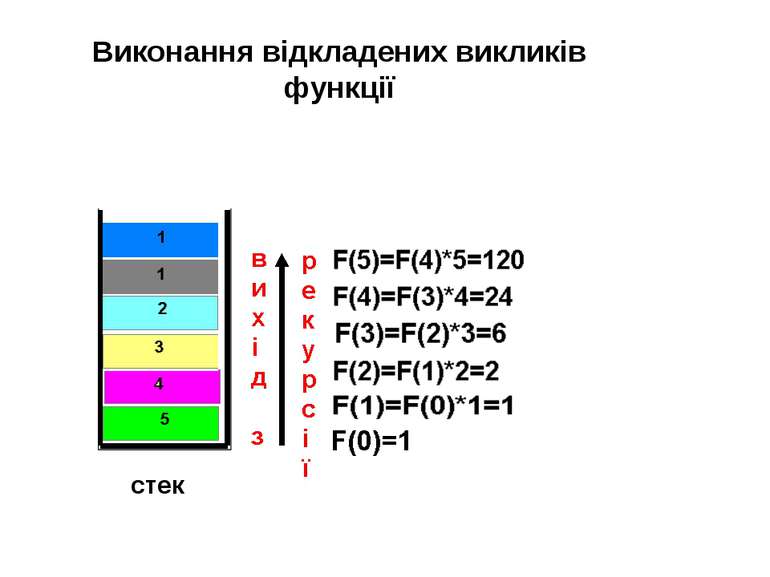
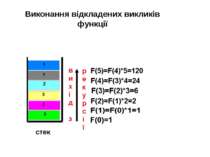
Виконання комп’ютером відкладених викликів функції можливе завдяки використанню стекa. Стек – модель оперативної пам’яті, де дані запам’ятовуються і зберігаються за принципом "перший прийшов – останнім вийшов" (аналогом стеку є ріжок для набоїв у автоматі).
Обчислення суми чисел від a до b з кроком 1 1)Звичайний спосіб: s:=0; for i:=a to b do s:=s+і; 2)Рекурсивний спосіб: Function Summa (a, b:integer):integer; begin If a=b then Summa :=a else Summa := Summa (a, b-1)+b еnd;
Обчислення степеня з натуральним показником хк 1)Звичайний спосіб: р:=1; for i:=1 to к do р=р*х ; 2)Рекурсивний спосіб: 1, при к = 0; Хк= хк-1, при к > 0. Function Power( k : integer; x : real) : integer; begin If k=0 then Power:=1 else Power:=Power(k-1, x) * х end;
Обчислення чисел Фібоначчі Fk= Fk-1 + Fk-2 , F1= F2=1 1)Звичайний спосіб: x:=1; z:=1; {-перші два числа Фібоначчі } for i:=1 to k do begin y:=x; x:=z; z:=x+y; write (z:5) end; 2)Рекурсивний спосіб: Function Fib (k:integer):integer; begin If k
Переваги використання рекурсії: рекурсивний алгоритм коротший і наглядніший. Недоліки: обчислення рекурсивного алгоритму на компютері потребує більше часу (за рахунок повторних звертань до підпрограми) і пам’яті (за рахунок дублювання локальних змінних підпрограми).
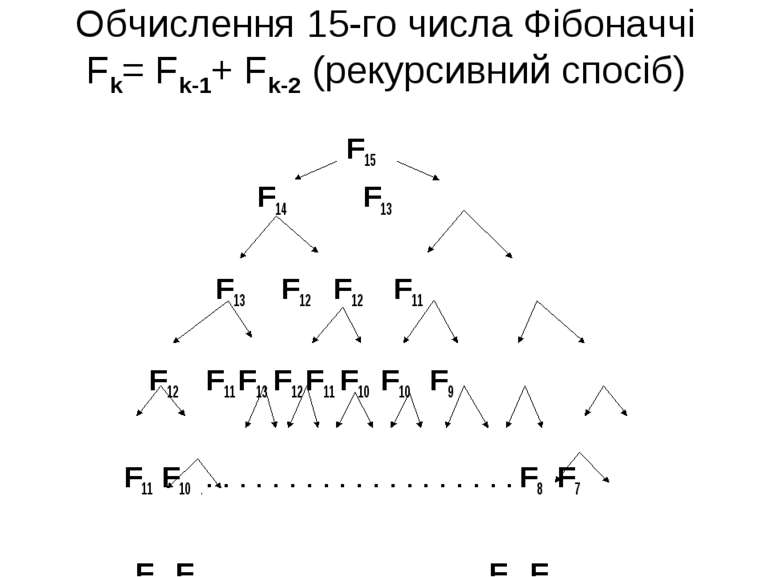
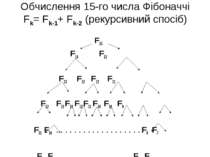
Обчислення 15-го числа Фібоначчі Fk= Fk-1+ Fk-2 (рекурсивний спосіб) F15 F14 F13 F13 F12 F12 F11 F12 F11 F13 F12 F11 F10 F10 F9 F11 F10 . . . . . . . . . . . . . . . . . . . . F8 F7 F9 F8 .. . . . . . . . . . . . . . . . F7 F6
Увага! При обчисленні 31-го числа Фібоначчі рекурсивним способом комп’ютер виконає >1 млн. операцій додавання, 45-го > 1 млрд.!!! (що може призвести до переповнення стеку). Для порівняння: обчислення за звичайним способом потребує 31 та 45 операцій додавання відповідно!
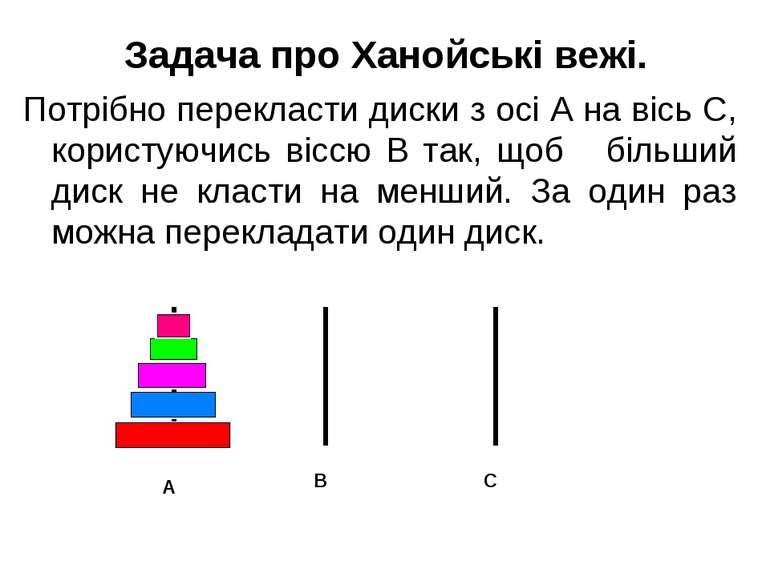
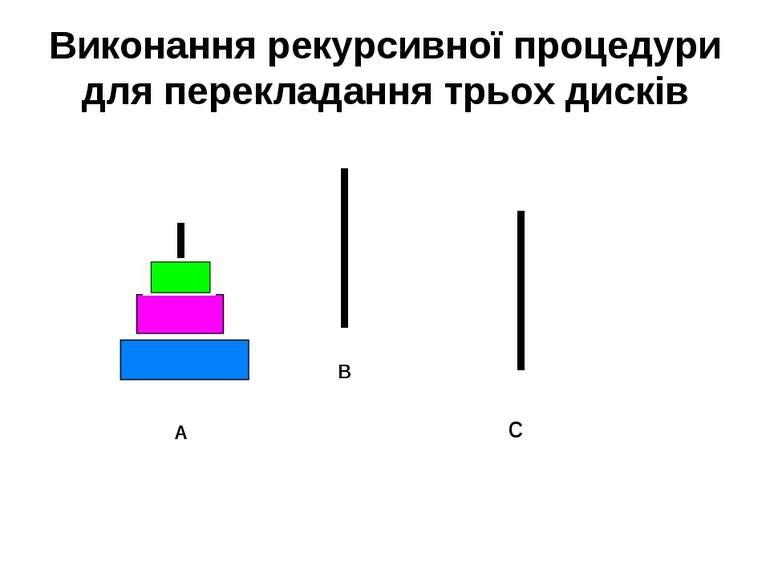
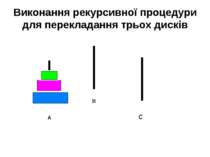
Задача про Ханойські вежі. Потрібно перекласти диски з осі А на вісь С, користуючись віссю В так, щоб більший диск не класти на менший. За один раз можна перекладати один диск. А В С
Програма procedure Xanoj(n : integer; A,B,C: char); begin If n=1 then writeln(‘перекласти диск з осі’, A, ’на вісь’, C) else begin Xanoj(n-1, A, B, C); writeln(‘перекласти диск з осі’, A, ’на вісь’, C) Xanoj(n-1, B, C, A); end end; {кінець процедури} Var n: integer ; begin writeln(‘задайте кількість дисків’); readln(n); Xanoj(n,’A’,’B’,’C’) end. {кінець головної програми}
Схожі презентації
Категорії