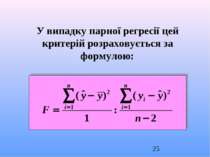Презентація на тему:
Верифікація моделі програми

Тема 3 Верифікація моделі Кафера інформатики та комп‘ютерних технологій доцент Бесклінська О.П.

Зміст Показники якості моделі 2. Перевірка значущості та довірчі інтервали

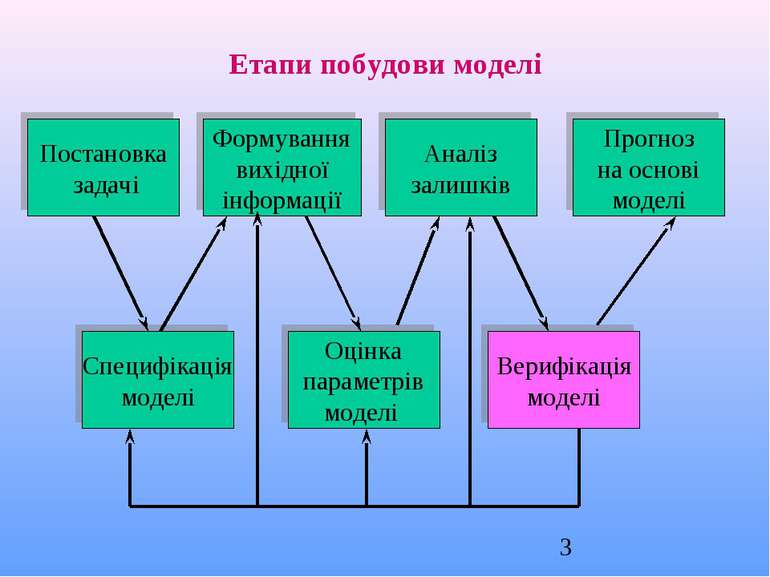
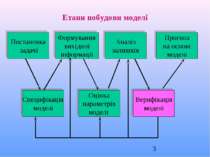
Постановка задачі Формування вихідної інформації Аналіз залишків Прогноз на основі моделі Специфікація моделі Оцінка параметрів моделі Верифікація моделі Етапи побудови моделі

1. Показники якості моделі Верифікація моделі—статистична перевірка на адекватність моделі, тобто наскільки добре розв‘язано проблему специфікації моделі, наскільки добрі оцінки імітаційних та прогнозних розрахунків.

Для перевірки коректності побудови моделі визначають: • стандартну похибку рівняння; • коефіцієнт детермінації; • коефіцієнт множинної кореляції; • стандартну похибку параметрів.

Стандартна похибка рівняння (точкова оцінка емпіричної дисперсії залишків)- характеризує абсолютну величину розкиду випадкової складової рівняння

Поправка на число ступенів свободи дає незміщену оцінку дисперсії залишків:

У поняття "тіснота зв'язку" (щільність) вкладається оцінка впливу незалежної змінної на залежну змінну. Під терміном "значимість зв'язку" (істотність, або значущість) розуміють оцінку відхилення вибіркових змінних від своїх значень у генеральній сукупності спостережень за допомогою статистичних критеріїв.

Коефіцієнт детермінації показує, якою мірою варіація залежної змінної (результативного показника) у визначається варіацією незалежної змінної (вхідного показника) х. де

Інші формули: де - розрахункові значення регресанда; -загальна середня фактичних даних результативного показника; -фактичні індивідуальні значення результативного показника.

квадрат емпіричного коефіцієнта кореляції між двома рядами спостережень (теоретичними значеннями регресанта та його розрахунковими значеннями ).

Коефіцієнт кореляції, або індекс кореляції, показує, наскільки значним є вплив змінної хi , на yi і розраховується так:

Іноді для спрощення розрахунків тісноту кореляційного зв'язку характеризують коефіцієнтом кореляції, який розраховується за формулою:

Якщо зв'язок між результативним і вхідним показниками лінійний, то використовується лінійний коефіцієнт кореляції, який характеризує не тільки тісноту зв'язку, а і його напрям:

2. Перевірка значущості та довірчі інтервали.

Зауваження. У задачах регресійного аналізу важливе значення має припущення про нормальний розподіл випадкових величин, що задіяні в даній моделі. Певні перетворення нормально розподілених величин забезпечують їх розподіл за законом Стьюдента чи за законом Фішера: на підставі першого з них визначаються довірчі інтервали, а другий дає змогу оцінювати відношення двох випадкових величин.

Стосовно кожного статистичного результату висувається так звана нульова гіпотеза (про рівність нулю деякої випадкової величини) і альтернативна до неї гіпотеза (про її суттєву відмінність від нуля). У нульовій гіпотезі формулюють результат, який бажано відхилити, а в альтернативній, яка інакше називається експериментальною, — той, що його необхідно підтвердити.

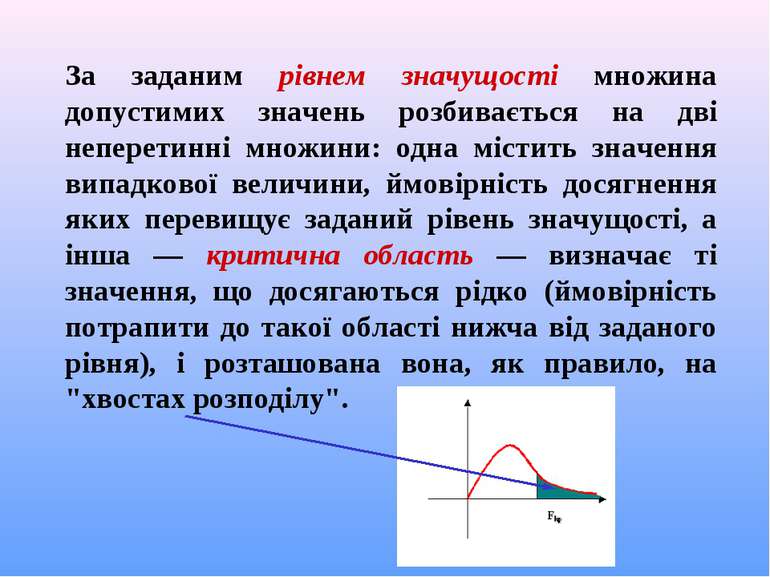
За заданим рівнем значущості множина допустимих значень розбивається на дві неперетинні множини: одна містить значення випадкової величини, ймовірність досягнення яких перевищує заданий рівень значущості, а інша — критична область — визначає ті значення, що досягаються рідко (ймовірність потрапити до такої області нижча від заданого рівня), і розташована вона, як правило, на "хвостах розподілу".

При перевірці гіпотез може бути допущена помилка, наприклад може бути відхилена нульова гіпотеза, хоча насправді вона правильна (помилка першого роду), або ж, навпаки, нульова гіпотеза може бути прийнята, хоча вона неправильна (помилка другого роду).

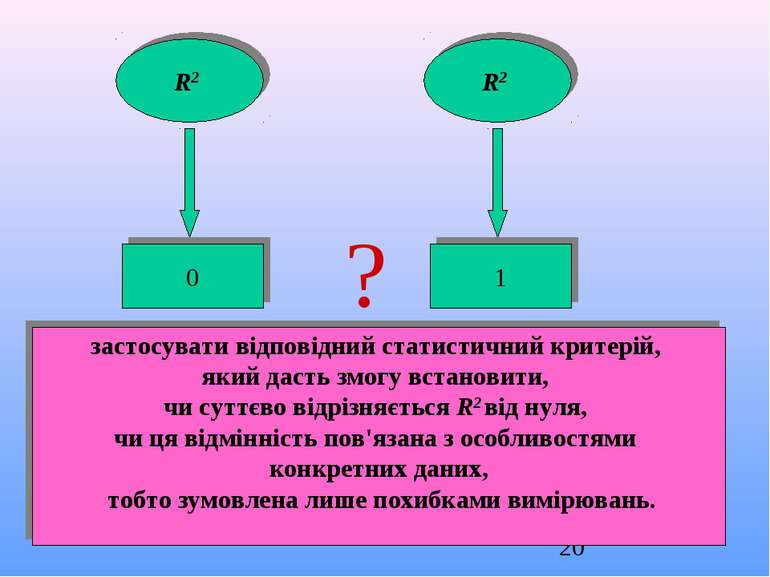
R2 R2 0 1 ? застосувати відповідний статистичний критерій, який дасть змогу встановити, чи суттєво відрізняється R2 від нуля, чи ця відмінність пов'язана з особливостями конкретних даних, тобто зумовлена лише похибками вимірювань.

Висувається нульова гіпотеза Н0 : R2 = О. Це означає, що досліджуване рівняння не пояснює змінювання регресанда під впливом відповідних регресорів. У такому разі всі коефіцієнти при незалежних змінних мають дорівнювати нулю. При цьому нульову гіпотезу можна подати у вигляді Н0 :а1 =а2 =... = аn = 0.

Альтернативною до неї є Н1: значення хоча б одного параметра моделі відмінне від нуля, тобто хоча б один із факторів впливає на змінювання залежної змінної.

Для перевірки цих гіпотез застосовують F- критерій Фішера з n-m-1 ступенями свободи. яке порівнюють з табличним значенням розподілу Фішера при заданому рівні значущості α. (Як правило, α = 0,05 або α = 0,01).

Якщо Fтабл < Fексп нульова гіпотеза відхиляється, тобто існує такий коефіцієнт у регресійному рівнянні, який суттєво відрізняється від нуля, а відповідний фактор впливає на досліджувану змінну.

У випадку парної регресії цей критерій розраховується за формулою:

Коефіцієнт кореляції, як вибіркова характеристика, перевіряється на значущість за допомогою t-критерію Стьюдента. Фактичне значення t статистики обчислюється за формулою

tексп порівнюється з табличним значенням t- розподілу з п – т – 1 ступенями свободи, та при заданому рівні значущості α/2 Якщо можна зробити висновок, що коефіцієнт кореляції достовірний (значущий), а зв'язок між залежною змінною та всіма незалежними факторами суттєвий.

Можна визначити стандартні похибки оцінок параметрів моделі з урахуванням дисперсії залишків: де - дисперсія залишків, обчислюється за формулою:

cjj –відповідний діагональний елемент матриці похибок С (матриця, обернена до матриці коефіцієнтів системи нормальних рівнянь)

Статистичну значущість кожного параметра моделі можна перевірити за допомогою t-критерію. При цьому нульова гіпотеза буде: Н0: aj=0, альтернативна H1: aj≠0 Експериментальне значення t-статистики для кожного параметра моделі обчислюється за формулою:

Довірчі інтервали для кожного параметра aj обчислюються на основі його стандартної похибки та критерію Стьюдента: Табличне значення t табл. , як і раніше, має n-m-1 ступенів свободи і рівень значущості α/2

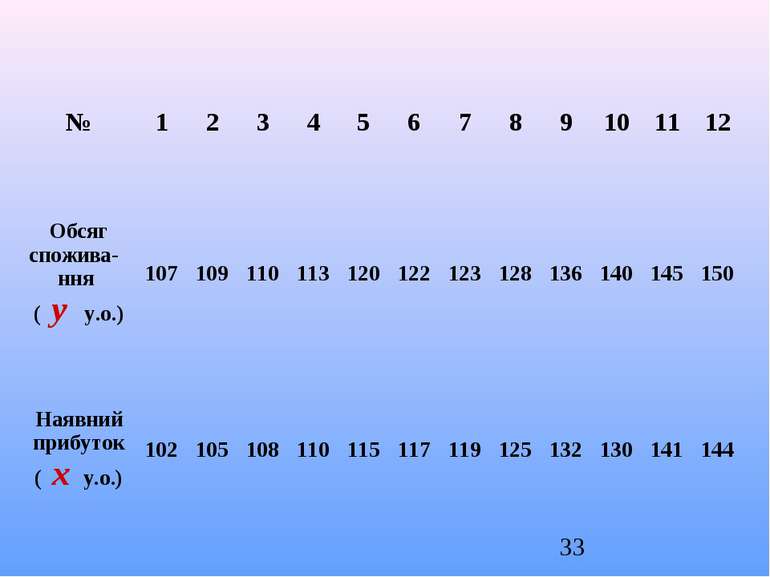
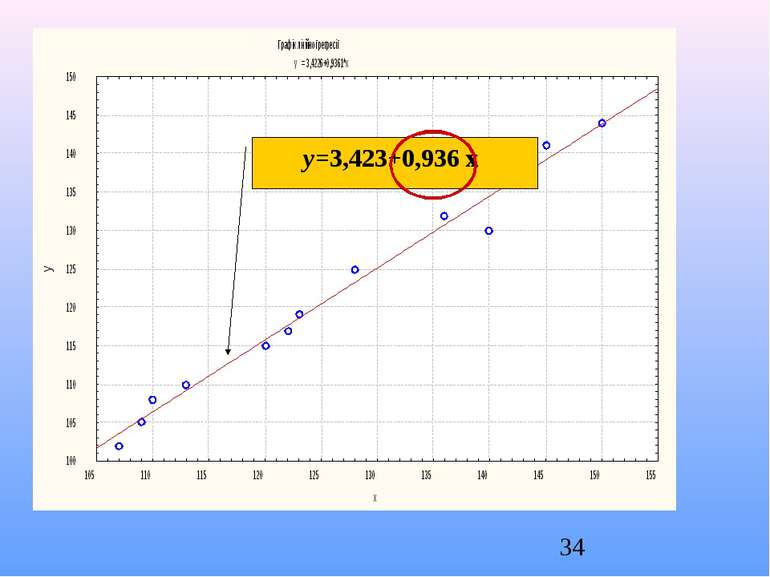
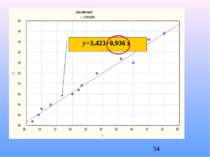
Завдання: Зробити аналіз залежності обсягу споживання y (у.о.) домогосподарства від наявного прибутку x (у.о.) за вибіркою обсягом n=12, результати якої наведено у таблиці. Визначити вид залежності, оцінити параметри рівняння регресії, оцінити силу лінійної залежності між x та y.

y=3,423+0,936 х

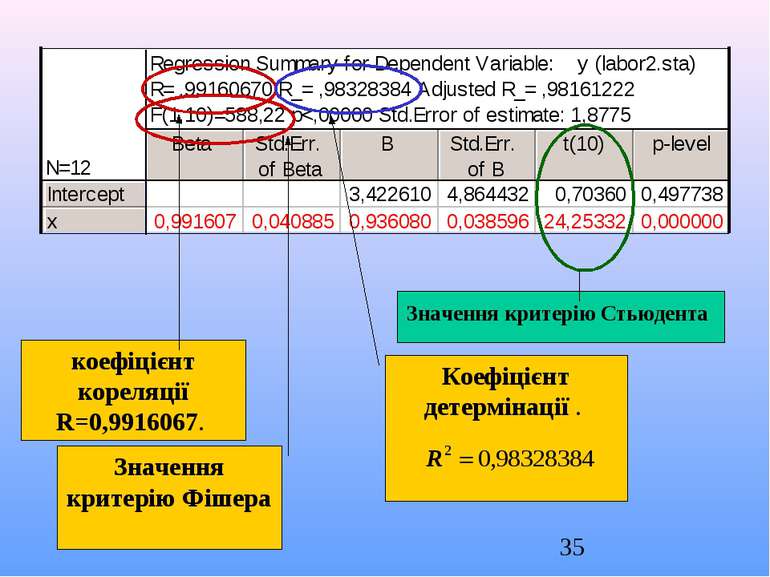
коефіцієнт кореляції R=0,9916067. Коефіцієнт детермінації . Значення критерію Фішера Значення критерію Стьюдента

Завдання : За 10 парами спостережень отримано такі результати: За МНК оцініть коефіцієнти рівняння регресії Y на X . Оцініть коефіцієнт кореляції rxy