Презентація на тему:
Основи нейромережевих технологій

Тема №12 Основи нейромережевих технологій

Нейронні мережі: загальний вступ Нейронні мережі, або штучні нейронні мережі, діють за принципами, подібними до принципів функціонування людського мозку. Конекціоністський підхід. Словесні, символьні знання не використовуються. Про пояснення не йдеться. Моделювання підсвідомого мислення.

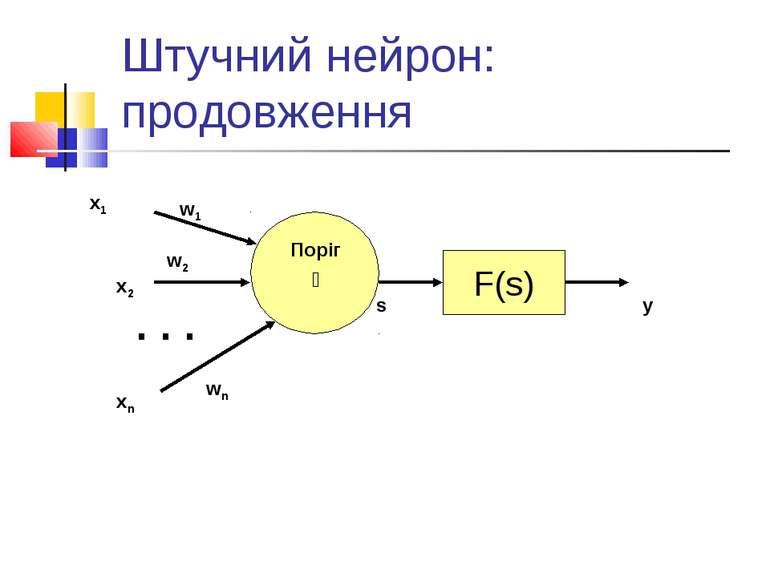
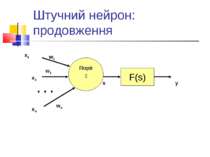
Нейронні мережі: базові поняття Штучний нейрон - деяка модель, яка імітує найважливіші риси природного нейрону, або реалізація такої моделі (апаратна або програмна). Нейронна мережа - сукупність взаємопов’язаних штучних нейронів. Основна ідея - навчання. Нейрокомп’ютер – комп’ютерна система, побудована за принципами, характерними для нейронних мереж. Програмні імітатори.

Нейронні мережі: основний принцип навчання Основний принцип навчання нейронної мережі полягає в налаштуванні зв’язків між нейронами: зміні коефіцієнтів зв’язків; перебудові структури тощо.

Основна характеристика нейромережевого алгоритму задання структури (топології) нейронної мережі; задання правила навчання.

Основні сфери застосування розпізнавання образів; кластерний аналіз; прогнозування; фільтрація; організація пам’яті.

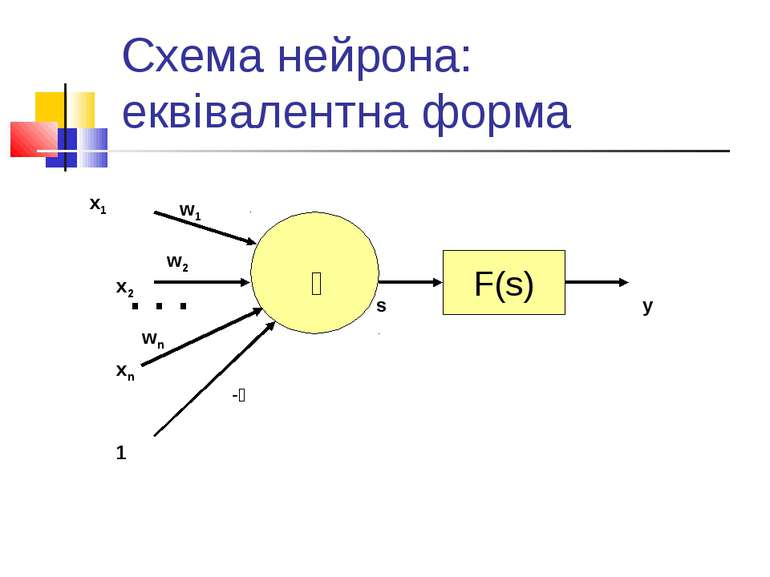
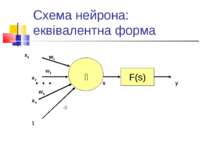
Модель штучного нейрона В основі - модель, запропонована Мак-Каллоком і Піттсом в 1943 р. (хоча і з рядом модифікацій).

Штучний нейрон: продовження x1 w1 . . . x2 w2 xn wn Поріг s F(s) y

Штучний нейрон: математика F(s) - активаційна функція

Схема нейрона: еквівалентна форма x1 w1 . . . x2 w2 xn wn s F(s) y 1 -

Навчання нейрона: основний принцип Основний принцип навчання нейрона полягає в корекції вагових коефіцієнтів.

Типові активаційні функції порогова: F(s)=1, якщо s 0; 0, якщо s0.

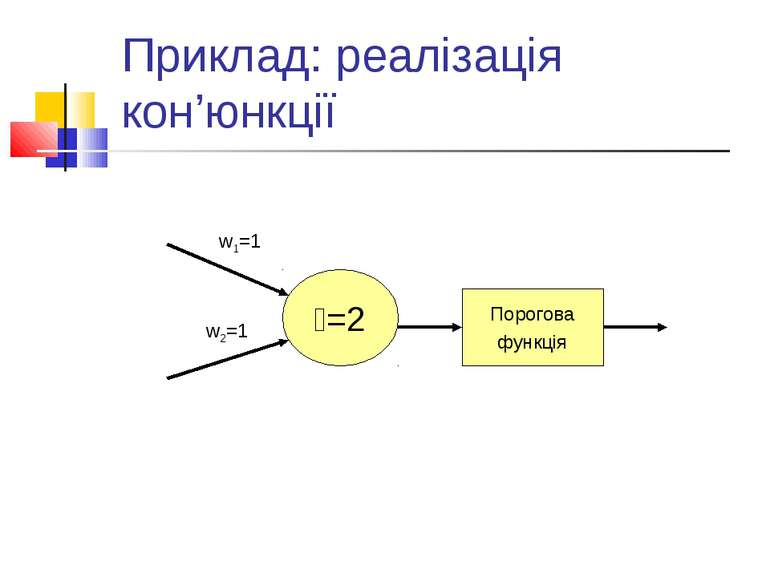
Нейрони Мак-Каллока і Піттса: ключовий результат Ключовий результат Мак-Каллока і Піттса: певним чином організована сукупність нейронів може обчислювати будь-яку обчислювану функцію.

Приклад: реалізація кон’юнкції =2 w1=1 w2=1 Порогова функція

Персептрон Розенблатта (1958 р) x1 x2 xn . . . S-елементи A-елементи R-елементи W

Алгоритми навчання: загальний огляд Досить однотипні за своєю природою; за своєю математичною суттю практично ідентичні згаданому раніше алгоритму персептрона. Основна ідея: корекція коефіцієнтів у випадку, якщо після пред’явлення чергового навчального вектора фактичний вихід не збігається з бажаним. Така корекція може здійснюватися після кожного пред’явлення чергового вектора.

Приклад: правило Уїдроу-Хопфа Інша назва - -правило. Для нейрона з лінійною функцією активації (ADALINE). wj:= wj + (d-y)xj , := - (d-y)

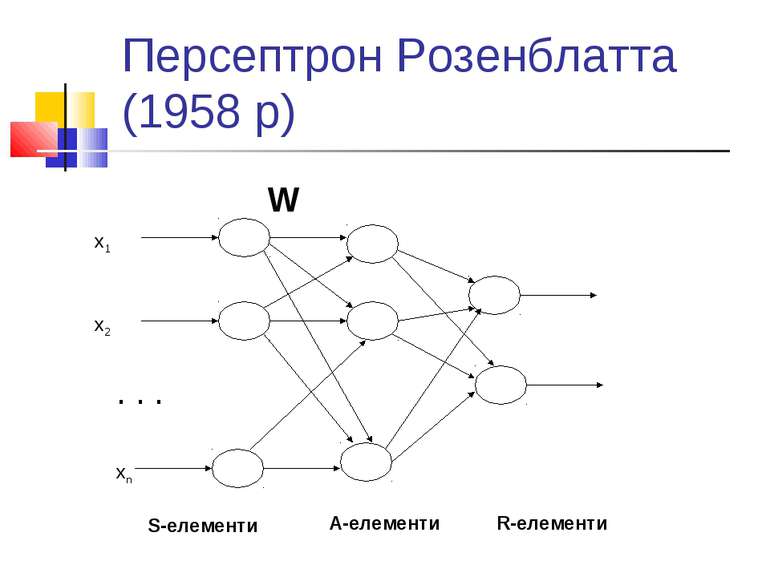
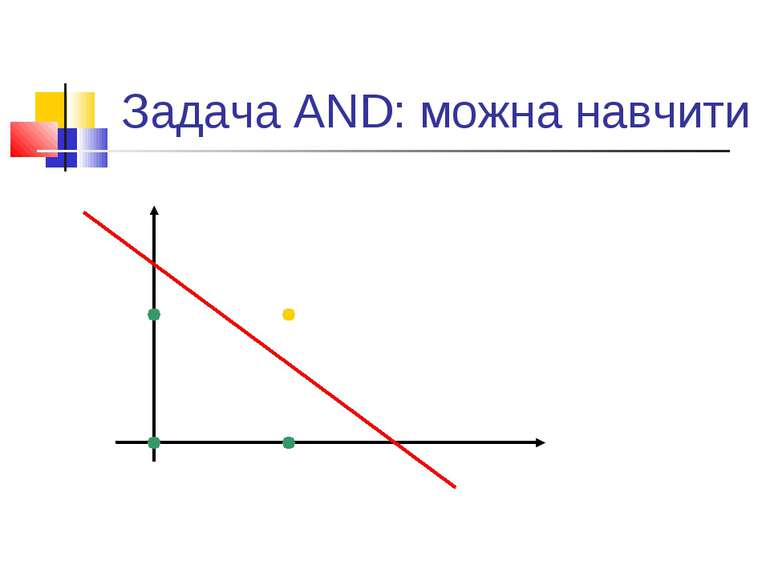
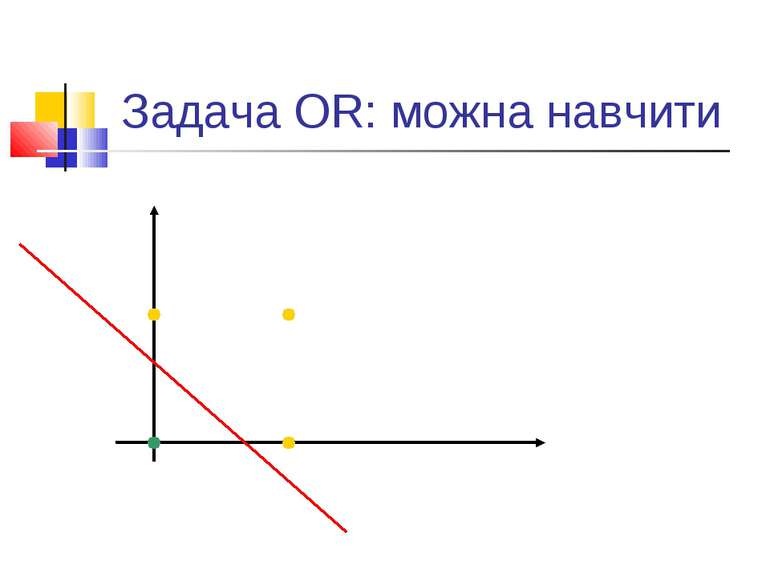
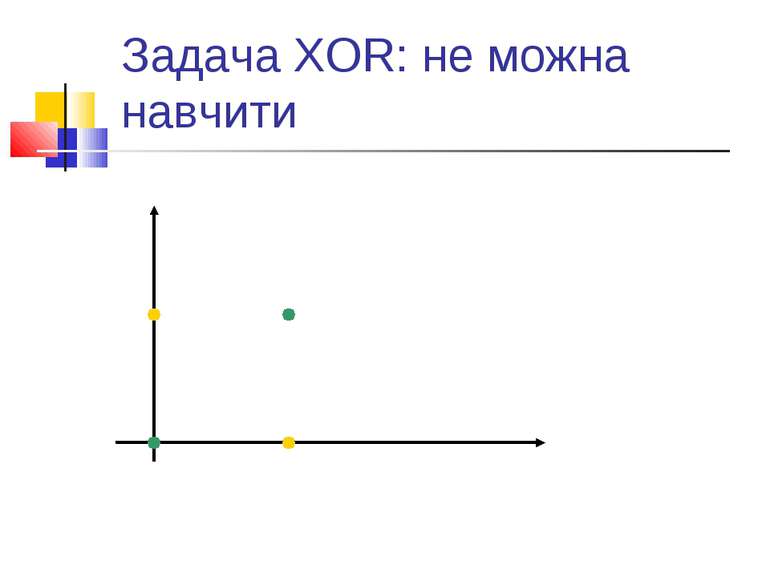
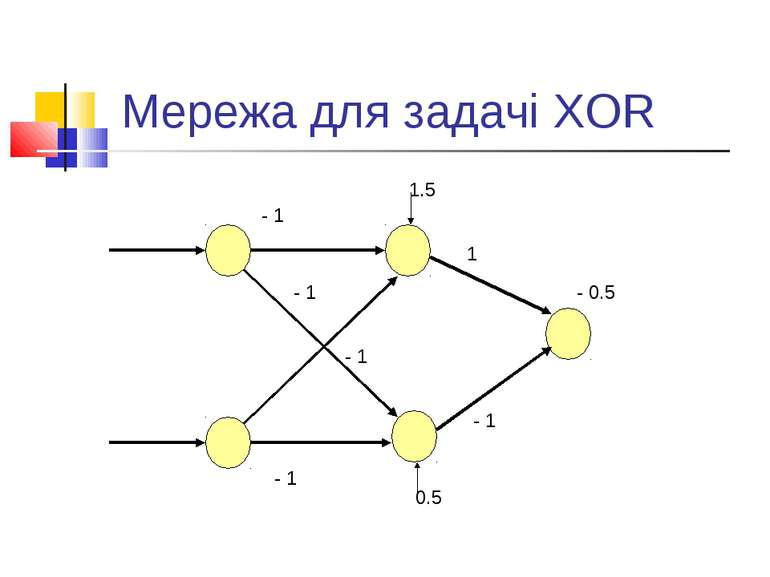
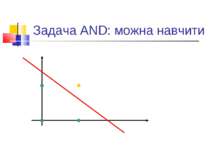
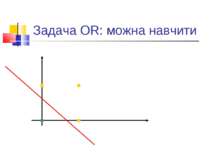
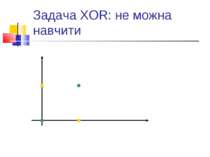
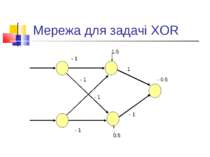
Обмеженість простих персептронів Ряд експериментів, в першу чергу - з розпізнавання. Аналіз Мінського і Пейперта: системи, подібні до персептронів, в принципі не можуть розв’язувати ряд задач. По суті - алгоритми навчання таких систем еквівалентні знаходженню лінійної розділяючої функції. Тобто - якщо є лінійне розділення, то алгоритм знайде коефіцієнти лінійної розділяючої функції. Якщо ні - то ні. Класичний приклад: задача XOR.

Задача AND: можна навчити

Задача OR: можна навчити

Задача XOR: не можна навчити

Сучасні нейронні мережі: загальний огляд З початку 80-х років – відновлення інтересу. Нові підходи та нові алгоритми навчання. Існує дуже багато напрямків. Ми розглянемо: багатошарові нейронні мережі; мережі Хопфілда; карти Кохонена.

Багатошарові нейронні мережі x1 x2 xn . . . W1 Wn y1 . . . . . . ym Сховані шари

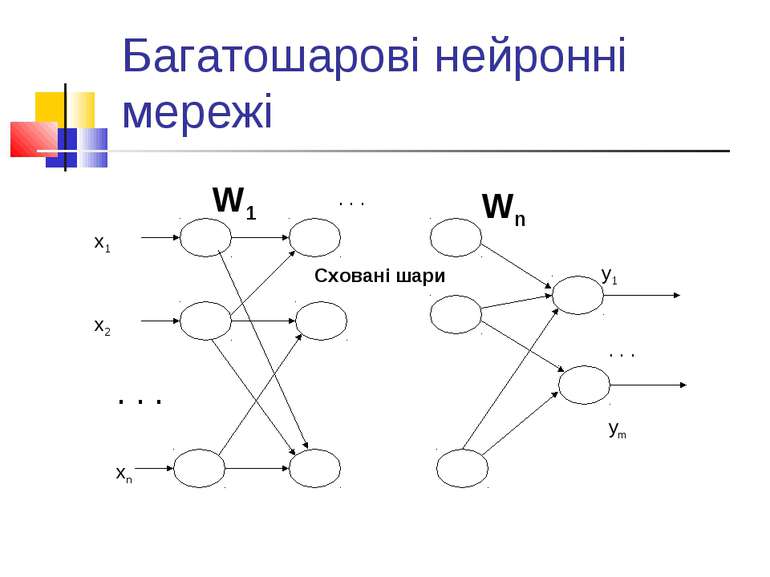
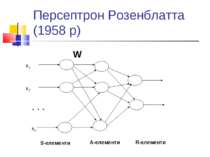
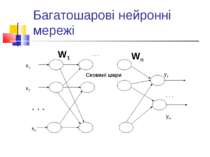
Багатошарові нейронні мережі: загальний опис Вхідний шар сприймає вхідні дані та розподіляє їх до наступного шару. Вихідний шар видає результати. Між ними - проміжні, або сховані шари. Вихід кожного нейрону попереднього шару з’єднаний з входами усіх нейронів наступного шару; wik - зв’язок між i-м нейроном попереднього шару та k-м нейроном наступного.

Багатошарові нейронні мережі: продовження Ключова ідея: багатошарові нейронні мережі можуть здійснювати нелінійне розділення. Класичний метод - метод зворотного розповсюдження помилок (back propagation). Активаційна функція не повинна бути лінійною. Часто використовуються, зокрема, сигмоїдні активаційні функції.

Основна теорема Будь-яка неперервна функція від n змінних може бути з довільною мірою точності наближена трьохшаровою нейронною мережею з одним схованим шаром. Нейронів на проміжному шарі має бути принаймні 2n+1. Теорема стверджує про принципову можливість, але не каже, якою саме має бути така мережа, зокрема якими мають бути активаційні функції. Взагалі, питання про кількість схованих шарів і кількість нейронів на них досліджені недостатньо.

Мережа для задачі XOR 0.5 1.5 - 0.5 - 1 - 1 - 1 - 1 - 1 1

Метод зворотного поширення помилок Файл neuron.doc. Недоліки: повільно сходиться; проблема локальних мінімумів.

Нейронні мережі: прогнозування Дано: послідовні значення випадкового процеса x1,…, xn. Потрібно: прогноз процесу; визначити xn+1.

Модель лінійної авторегресії

Входи і виходи мережі Входи: xn-p, … , xn-1. Вихід: xn.

Мережі Хопфілда Використовуються перш за все для запам’ятовування образів; асоціативна пам’ять. Але мережа Хопфілда може застосовуватися і для розпізнавання.

Архітектура і функціонування: загальний принцип Архітектура - кожний нейрон зв’язаний один з одним; матриця вагових коефіцієнтів - X’X-I, X-матриця даних. При подачі вхідного вектора мережа функціонує, поки вихід не перестане змінюватися. Тоді він буде дорівнювати одному з образів, які були занесені до пам’яті.

Мережа Хопфілда: більш детальний опис роботи Вхідний вектор (x1, … xn) встановлює початкові значення всіх елементів. Елемент вхідного вектора для оновлення вибирається випадковим чином; вибраний елемент змінює свій стан на основі зваженої суми сигналів від інших елементів: (x1t+1, … xnt+1) -> (x1t, … xnt) . xi t+1:= F( xi twji ); Вибирається інший елемент, і процес повторюється. Критерій завершення – коли жодний з елементів, вибраних для оновлення, не змінює свого значення.

Принцип мінімізації енергії Кажуть, що мережа Хопфілда мінімізує енергію зв’язків між нейронами

Характерний експеримент Розпізнавання літер “А”, “Б”, “Н”, “И” – спочатку незашумлених, потім зашумлених (10%, 20% і т.п).