Презентація на тему:
Нормальні алгоритми Маркова

Нормальні алгорифми Маркова

Біографія А.А.Маркова Марков Андрій Андрійович (молодший) (22 вересня 1903, Санкт-Петербург, Російська імперія — 11 жовтня 1979, Москва, РРФСР) — радянський математик, син відомого російського математика А. А. Маркова, засновник радянської школи конструктивної математики. Закінчив Восьму Петербурзьку гімназію в 1919 році; Ленінградський державний університет у 1924 році; аспірантуру в Астрономічному інституті в Ленінграді в 1928 році. Науковий ступінь доктора фізико-математичних наук присуджена без захисту дисертації в 1935 році. З 1959 по 1979 рік — завідувач кафедри математичної логіки Московського державного університету. Основні праці - з теорії динамічних систем, топології, топологічної алгебри, теорії алгоритмів і конструктивній математиці. Довів нерозв'язність проблеми рівності в асоціативних системах (1947), проблеми гомеоморфії в топології (1958), створив школу конструктивної математики і логіки в СРСР. Є автором Принципу Маркова, Нормального алгоритму Маркова, Теореми Маркова-Какутані і Теореми Ріса-Маркова-Какутані .

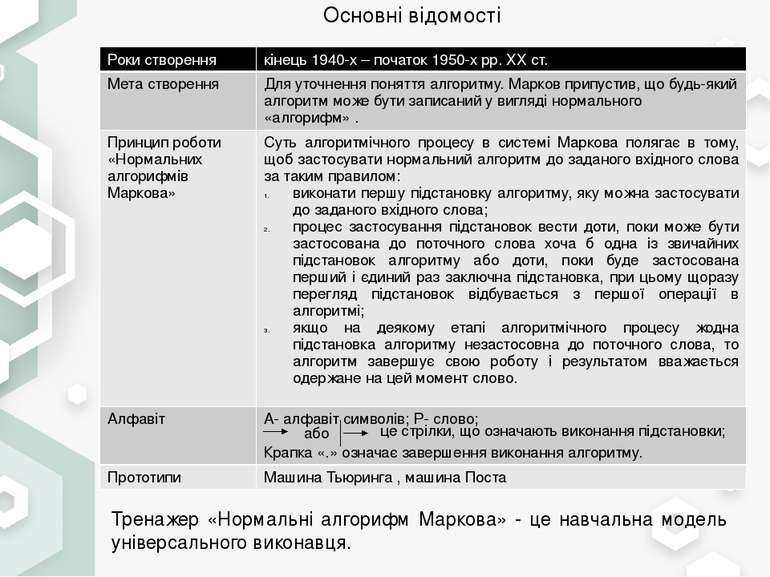
Основні відомості або це стрілки, що означають виконання підстановки; Тренажер «Нормальні алгорифм Маркова» - це навчальна модель універсального виконавця. Рокистворення кінець1940-х – початок 1950-хрр. ХХ ст. Мета створення Для уточнення поняття алгоритму.Марковприпустив, що будь-який алгоритм може бути записаний у вигляді нормального «алгорифм» . Принцип роботи«НормальнихалгорифмівМаркова» СутьалгоритмічногопроцесувсистеміМарковаполягаєв тому,щобзастосуватинормальнийалгоритм дозаданоговхідногослова за таким правилом: виконатипершупідстановкуалгоритму, якуможназастосуватидозаданоговхідногослова; процесзастосуванняпідстановоквестидоти,покиможебутизастосованадо поточного словахочаб однаіззвичайнихпідстановокалгоритмуабодоти,покибудезастосованаперший ієдинийраззаключнапідстановка, прицьомущоразупереглядпідстановоквідбуваєтьсязпершоїопераціївалгоритмі; якщонадеякомуетапіалгоритмічногопроцесужоднапідстановкаалгоритмунезастосовнадо поточного слова, то алгоритмзавершуєсвою роботу і результатомвважаєтьсяодержаненацеймомент слово. Алфавіт А- алфавіт символів; Р- слово; Крапка «.» означає завершення виконання алгоритму. Прототипи МашинаТьюринга, машинаПоста

Правила виконання НАМ Береться будь-який непорожній рядок символів алфавіту. Він вважається вхідним словом Р алгоритму. Робота НАМ складається з послідовності однотипних кроків. Крок роботи алгоритму може бути описаний таким чином: 1. У впорядкованій послідовності підстановок шукається найперша підстановка, ліва частина якої входить в слово Р. 2. У слові Р шукаємо найперше (ліве) входження лівого слова знайденої підстановки. 3. Це входження в слово Р замінюємо на праву частину знайденої підстановки (тобто виконується перетворення даних згідно знайденої формули підстановки). Отримуємо нове слово Р'. 4. На наступному кроці це слово Р' розглядається як початкове і до нього застосовується та ж сама процедура. Таким чином, вхідне слово Р на кожному кроці перетворюється, утворюючи нове слово.Слід звернути особливу увагу на той факт, що на кожному кроці формули в НАМ завжди переглядаються починаючи з найпершої.

Умови роботи НАМ Якщо на черговому кроці була застосована звичайна формула підстановки то робота НАМ продовжується. Якщо на черговому кроці була застосована завершуюча формула підстановки, то після її застосування робота НАМ припиняється. Слово, отримане в цей момент, є вихідним словом, тобто результатом застосування НАМ до вхідного слова. Різниця між звичайною і завершальною формулами підстановки полягає в тому, що після застосування звичайної формули робота НАМ продовжується, а після завершальної формули - припиняється. Якщо на черговому кроці до поточного слова не застосовна жодна формула, то і в цьому випадку робота НАМ припиняється, а вихідним словом вважається поточне слово. Таким чином, НАМ зупиняється в двох випадках: або була застосована завершуюча формула підстановки, або жодна з формул не може бути застосована. Обидва ці випадки вважаються «хорошим» закінченням роботи НАМ. У обох випадках говорять, що НАМ застосовний до вхідного слова. Проте може трапитися і так, що НАМ ніколи не зупиниться. Це відбувається, коли на кожному кроці є застосовна формула і ця формула звичайна. Тоді говорять, що НАМ незастосовний до вхідного слова. В цьому випадку ні про який результат немає і мови.

Приклади нормальних алгоритмів Маркова Алгоритм завершує роботу, оскільки жодне правило не може бути застосоване. Його застосування до слова «abbbcaa» послідовно дало слова: «abbbca», «abbca» і «abca», після чого виконання НАМ завершилося.

Отже, всяке слово в алфавіті A, що містить хоч би одне входження букви а, алгоритм переробляє в вихідне слово викреслюванням в ньому найлівішого (першого) входження букви а. Порожнє слово алгоритм перетворює в порожнє. Алгоритм не застосовний до слів, які містять тільки букву b.