Презентація на тему:
Закони Кеплера – закони руху небесних тіл

Закони Кеплера – закони руху небесних тіл

З прадавніх часів вважалося, що небесні тіла рухаються по "ідеальних кривих" - колах. Геоцентрична система Птолемея Клавдій Птолемей (біля 90 – 160 рр)

Микола Коперник, творець геліоцентричної системи світу, круговий рух також не ставив під сумнів. Микола Коперник (1473–1543) Геліоцентрична система світу Коперника

Однак спостережуване положення планет не відповідало обчисленому згідно теорії кругового руху планет навколо Сонця. Чому? У XVII столітті відповідь на це питання шукав німецький астроном Йоганн Кеплер.

Йоганн Кеплер (1571–1630 ) Тихо Браге (1546-1601) Йоганн Кеплер, вивчаючи рух Марса за результатами багаторічних спостережень датського астронома Тихо Браге, виявив, що орбіта Марса не коло, а має форму еліпса.

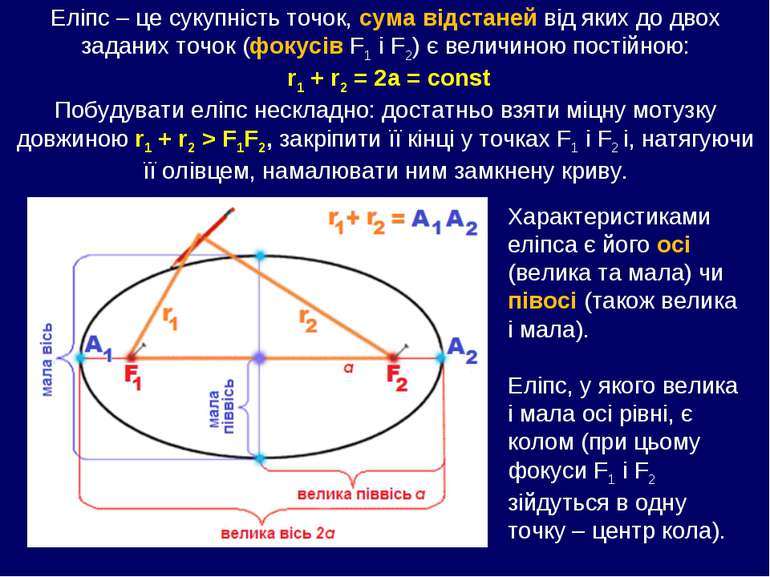
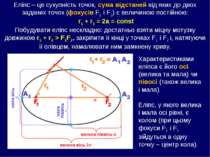
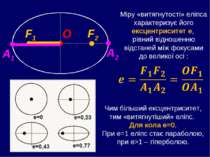
Еліпс – це сукупність точок, сума відстаней від яких до двох заданих точок (фокусів F1 і F2) є величиною постійною: r1 + r2 = 2a = const Побудувати еліпс нескладно: достатньо взяти міцну мотузку довжиною r1 + r2 > F1F2, закріпити її кінці у точках F1 і F2 і, натягуючи її олівцем, намалювати ним замкнену криву. Характеристиками еліпса є його осі (велика та мала) чи півосі (також велика і мала). Еліпс, у якого велика і мала осі рівні, є колом (при цьому фокуси F1 і F2 зійдуться в одну точку – центр кола).

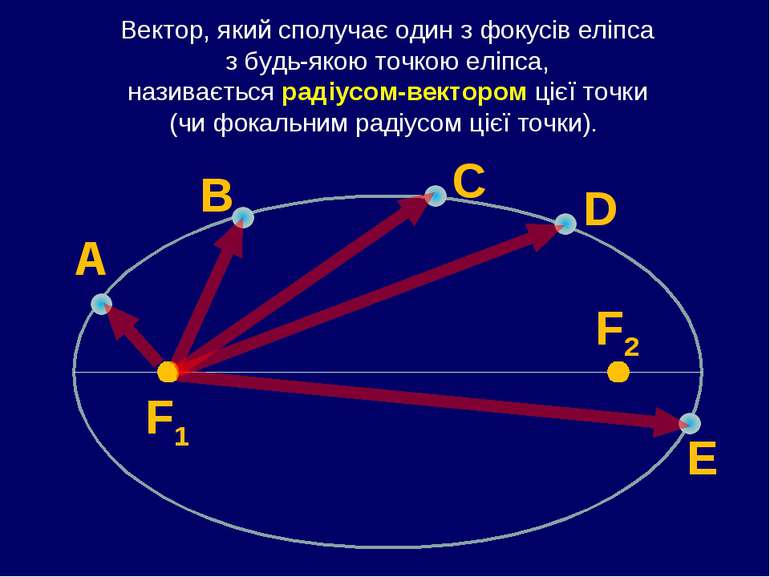
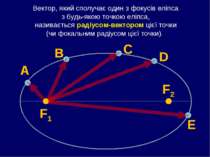
Вектор, який сполучає один з фокусів еліпса з будь-якою точкою еліпса, називається радіусом-вектором цієї точки (чи фокальним радіусом цієї точки). F1 F2 А В С D E

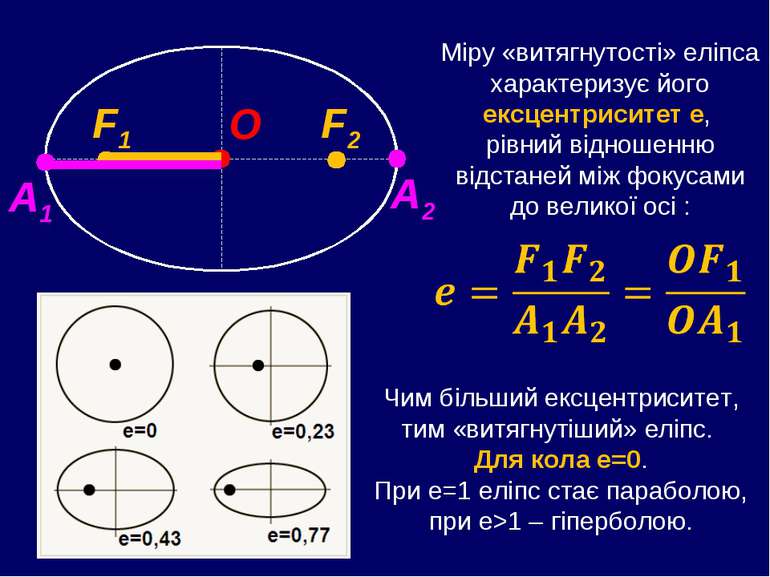
Міру «витягнутості» еліпса характеризує його ексцентриситет е, рівний відношенню відстаней між фокусами до великої осі : Чим більший ексцентриситет, тим «витягнутіший» еліпс. Для кола е=0. При е=1 еліпс стає параболою, при е>1 – гіперболою.

Кеплер дослідив рухи усіх відомих на той час планет і емпірично вивів три закони руху планет відносно Сонця. Ці закони можна застосовувати не лише до руху планет, але і до руху їх природних чи штучних супутників.

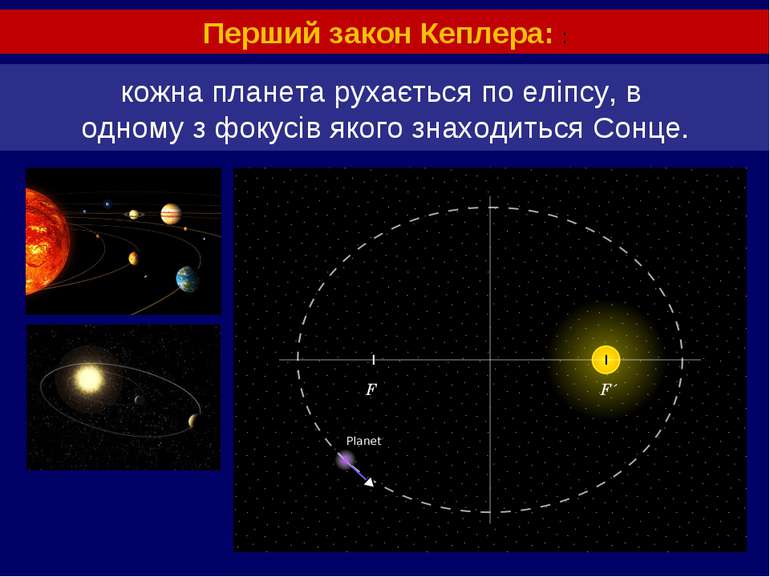
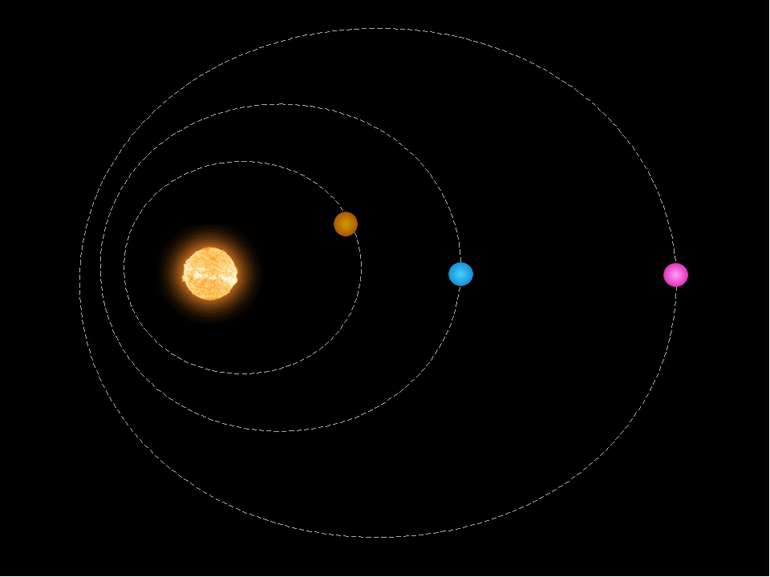
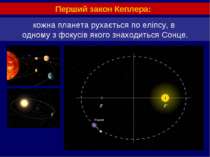
кожна планета рухається по еліпсу, в одному з фокусів якого знаходиться Сонце. Перший закон Кеплера: :

Орбіти планет - еліпси, які мало відрізняються від кіл, оскільки їх ексцентриситети дуже малі. Планета Ексцентриситет Меркурій 0,206 Венера 0,007 Земля 0,017 Марс 0,093 Планета Ексцентриситет Юпітер 0,049 Сатурн 0,057 Уран 0,046 Нептун 0,011

Велика піввісь орбіти планети - це її середня відстань від Сонця. Середня відстань Землі від Сонця прийнята в астрономії за одиницю відстані і називається астрономічною одиницею: 1 а.о. = 149 600 000 км ≈ 150 000 000 км Найближчу до Сонця точку орбіти називають перигелієм (грец. пері - біля, поблизу; Геліос - Сонце), а найбільш віддалену - афелієм (грец. аф - вдалині).

Земля проходить перигелій своєї орбіти взимку, 2-5 січня (в цей час вона найближче наближається до Сонця), а афелій – влітку, 2-6 липня (в цей час вона перебуває на найбільшій відстані від Сонця). Відстань від Землі до Сонця в перигелії – 147 098 290 км, а в афелії – 152 098 232 км. В таблиці наведені дати і час проходження Землею перигелію та афелію у різні роки. Рік Перигелій Афелій 2010 3 січня, 00 год. 6 липня, 12 год. 2012 5 січня, 01 год. 5 липня, 04 год. 2014 4 січня, 12 год. 4 липня, 00 год. 2016 2 січня, 23 год. 4 липня, 16 год. 2018 3 січня, 06 год. 6 липня, 16 год.

По еліпсах рухаються не лише планети, але і їх природні чи штучні супутники. Найближча до Землі точка орбіти Місяця чи штучного супутника Землі називається перигеєм (грец. Гея - Земля), а найбільш віддалена - апогеєм.. Відстань Земля-Місяць в перигеї становить 356 400 км, а в апогеї – 406 700 км.

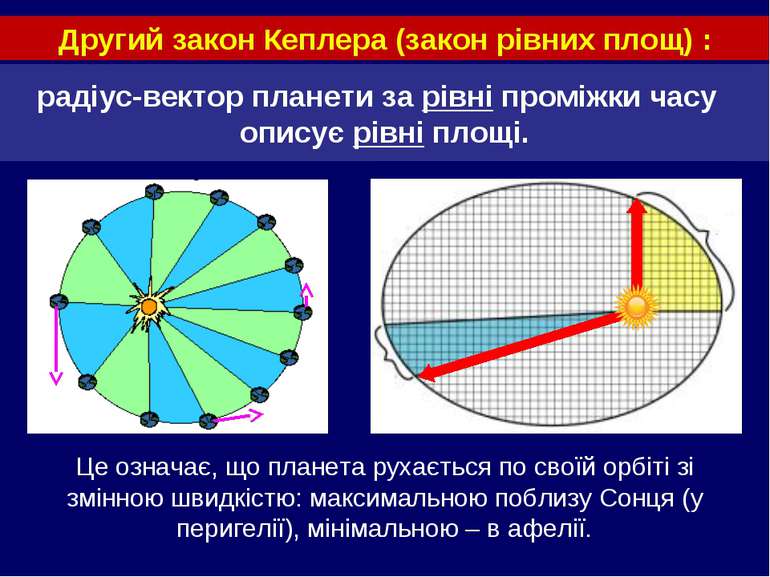
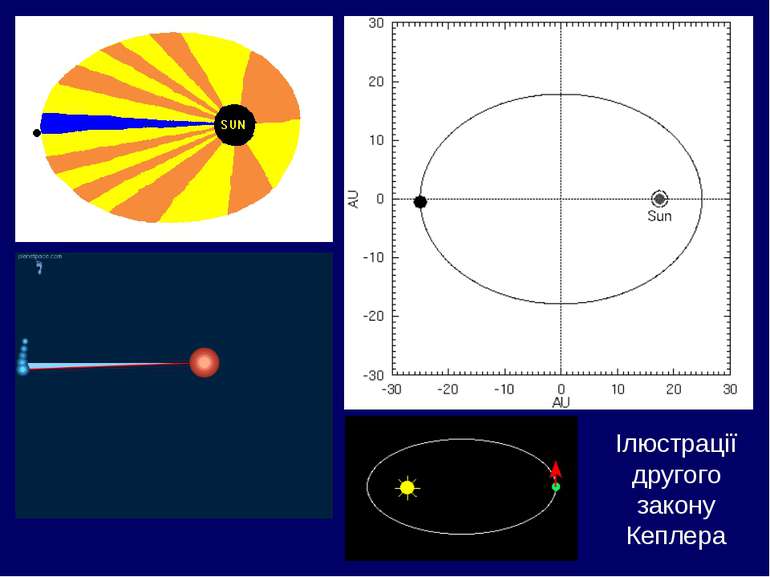
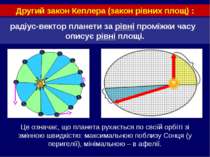
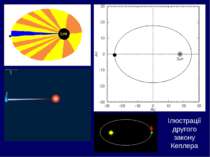
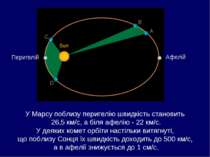
радіус-вектор планети за рівні проміжки часу описує рівні площі. Другий закон Кеплера (закон рівних площ) : Це означає, що планета рухається по своїй орбіті зі змінною швидкістю: максимальною поблизу Сонця (у перигелії), мінімальною – в афелії.

Ілюстрації другого закону Кеплера

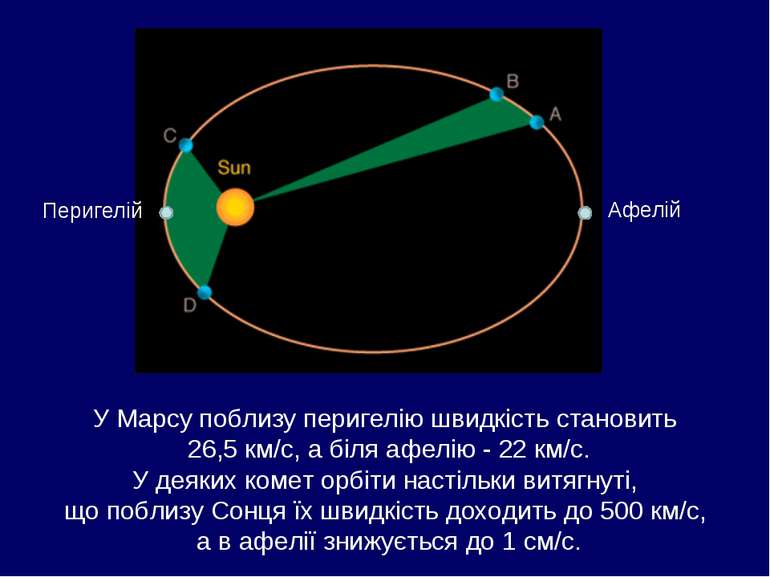
Перигелій Афелій У Марсу поблизу перигелію швидкість становить 26,5 км/с, а біля афелію - 22 км/с. У деяких комет орбіти настільки витягнуті, що поблизу Сонця їх швидкість доходить до 500 км/с, а в афелії знижується до 1 см/с.

Квадрати сидеричних періодів обертання двох планет відносяться як куби великих півосей їх орбіт : Третій закон Кеплера : Сидеричним періодом обертання планети називають час повного оберту планети навколо Сонця відносно зір. Цей закон можна застосувати як до планет, так і до їх супутників.

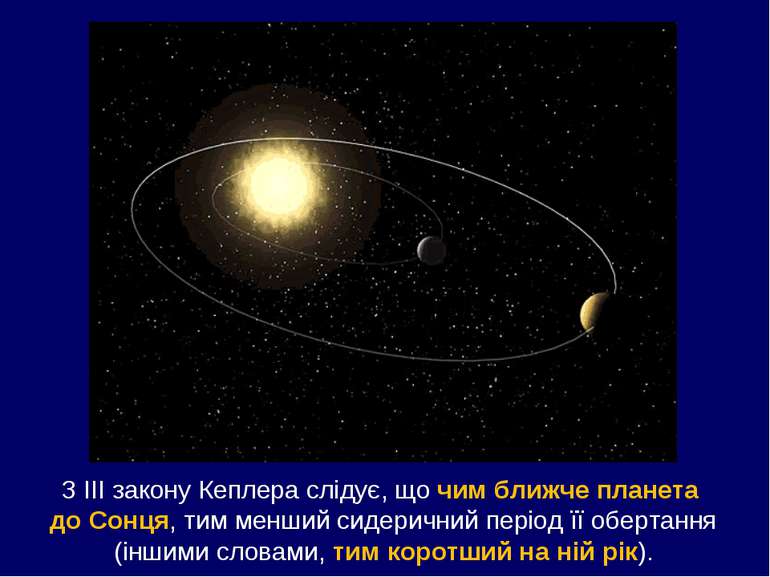
З ІІІ закону Кеплера слідує, що чим ближче планета до Сонця, тим менший сидеричний період її обертання (іншими словами, тим коротший на ній рік).

Квадрати сидеричних періодів обертання двох планет відносяться як куби великих півосей їх орбіт. Кожна планета рухається по еліпсу, в одному з фокусів якого є Сонце. Перший закон Кеплера Радіус-вектор планети за рівні проміжки часу описує рівні площі. Другий закон Кеплера Третій закон Кеплера

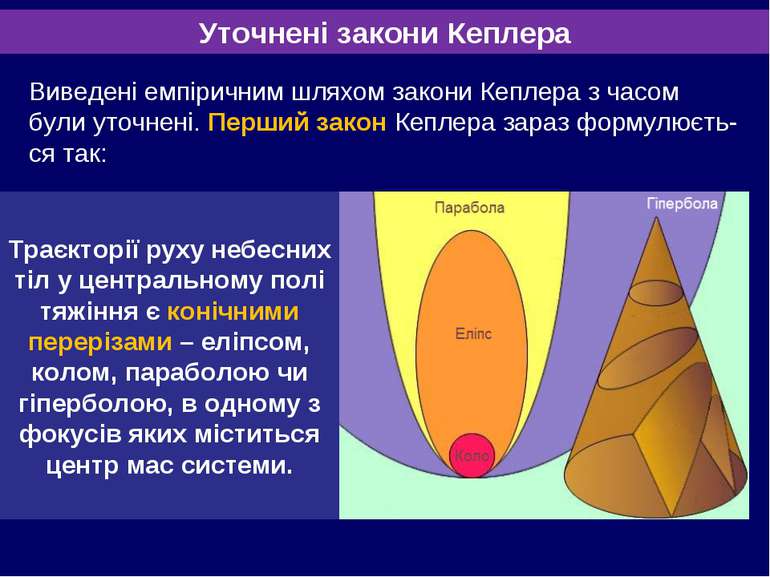
Уточнені закони Кеплера Виведені емпіричним шляхом закони Кеплера з часом були уточнені. Перший закон Кеплера зараз формулюєть-ся так: Траєкторії руху небесних тіл у центральному полі тяжіння є конічними перерізами – еліпсом, колом, параболою чи гіперболою, в одному з фокусів яких міститься центр мас системи.

Уточнені закони Кеплера Піддався уточненню і третій закон Кеплера, який зараз формулюється так: Добуток сум мас небесних тіл і їх супутників із квадратами сидеричних періодів обертання цих супутників відносяться як куби великих півосей їх орбіт. M1, m1 – маса одного небесного тіла та його супутника, M2, m2 – маса іншого небесного тіла та його супутника.