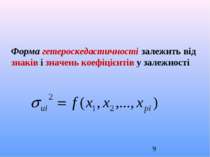Презентація на тему:
ГЕТЕРОСКЕДАСТИЧНІСТЬ У ІНФОРМАТИЦІ

Тема 6 ГЕТЕРОСКЕДАСТИЧНІСТЬ Кафера інформатики та комп‘ютерних технологій доцент Бесклінська О.П.

Зміст Виявлення гетероскедастичності та її природа. 2. Тестування наявності гетероскедастичності. 3. Алгоритм для параметричного тесту Гольдфельда-Квандта. 4. Трансформування початкової моделі. 5. Приклад застосування параметричного тесту Гольдфельда-Квандта.

Передумови МНК (умови Гаусса—Маркова) 1. Математичне сподівання випадкових відхилень ui повинно дорівнювати нулю: М(ui) = 0, (i=1,n). 2. Дисперсія випадкових відхилень ui має бути сталою величиною: 3. Випадкові відхилення ui та uj, i j мають бути незалежними один від одного.

4. Випадкові відхилення повинні бути незалежними від пояснювальних змінних X. 5. Випадкові відхилення ui повинні мати нормальний закон розподілу ui ~ N(0, u) . 6. Економетричні моделі мають бути лінійними відносно своїх параметрів.

1. Виявлення гетероскедастичності та її природа Розглянемо класичну лінійну багатофакторну модель

Означення. Якщо дисперсія залишків стала для кожного спостереження, то це явище називається гомоскедастичністю: Якщо це припущення не задовольняється в якомусь окремому випадку, то маємо гетероскедастичність (помилки ui некорельовані, але мають несталу дисперсію).

Означення. Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, то це явище називається гетероскедастичністю:

Сутність припущення про гомоскедастичність полягає в тому, що варіація кожної випадкової складової ui навколо її математичного сподівання не залежить від значення факторів х:

Форма гетероскедастичності залежить від знаків і значень коефіцієнтів у залежності

Оскільки ui — не спостережувана випадкова величина, ми не знаємо справжньої форми гетероскедастичності. В разі простої лінійної регресії гетероскедастичність має форму (k—const, яку потрібно оцінити)

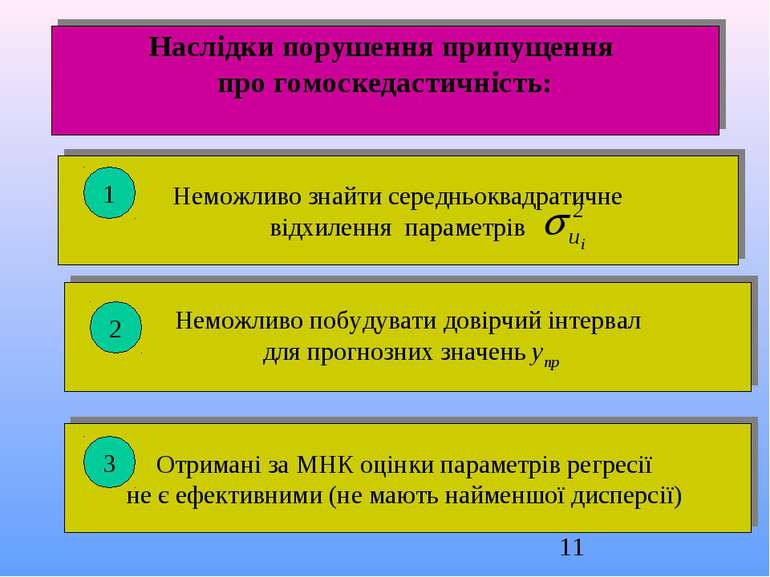
Наслідки порушення припущення про гомоскедастичність: Неможливо знайти середньоквадратичне відхилення параметрів Неможливо побудувати довірчий інтервал для прогнозних значень упр Отримані за МНК оцінки параметрів регресії не є ефективними (не мають найменшої дисперсії) 1 2 3

Тестування наявності гетероскедастичності Критерій Параметричний тест Гольдфельда-Квандта Непараметричний тест Гольдфельда-Квандта Тест Глейзера

Алгоритм для параметричного тесту Гольдфельда-Квандта Спостереження (вихідні дані) впорядкувати відповідно до величини елементів вектора Хi , який може викликати зміну дисперсії залишків 1 Відкинути спостережень, які знаходяться в середині векторів вихідних даних (n – кількість елементів вектора xi ) 2

Побудувати дві моделі на основі звичайного МНК по двох створених сукупностях спостережень за умови що (де m - кількість змінних) 3

Знайти суму квадратів залишків S1 і S2 по першій і другій моделях: де u1 і u2 - залишки відповідно за першою і другою моделями. 4

Розрахувати критерій який при виконанні гіпотези про гомоскедастичність буде відповідати F-розподілу з ступенями свободи 5а

Значення критерію R порівняти з табличним значенням F-критерію при вибраному рівні довіри і відповідних ступенях свободи; якщо R Fтабл , то гетероскедастичність відсутня 5б

4. Трансформування початкової моделі. Припустимо, що за статистичними даними побудовано початкову регресійну модель і на базі будь-якого тесту встановлено наявність гетероскедастичності:

Для усунення гетероскедастичності початкову модель змінюють (трансформують) так, щоб помилки мали сталу дисперсію: Трансформація моделі зводиться до зміни початкової форми моделі методом, який залежить від специфічної форми гетероскедастичності, тобто від форми залежності між дисперсіями залишків і значеннями незалежних змінних:

Нехай початкова модель де компоненти випадкового вектора и гетероскедастичні, але відповідають іншим класичним припущенням лінійної регресії. Припустимо, що гетероскедастичність має форму Трансформація моделі здійснюється діленням її на

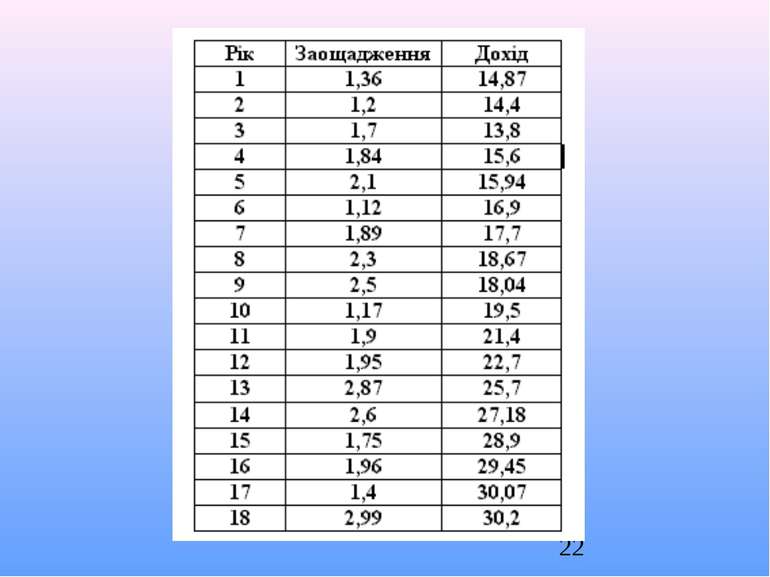
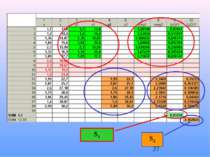
5. Приклад застосування параметричного тесту Гольдфельда-Квандта (1965) Приклад. Перевірити гіпотезу про відсутність гетероскедастичності для побудови моделі, яка характеризує залежність заощаджень від доходів населення. Статистичні дані наведено в таблиці.

Розв'язання. Ідентифікуємо змінні: у — заощадження, х — дохід. Специфікуємо модель у вигляді:

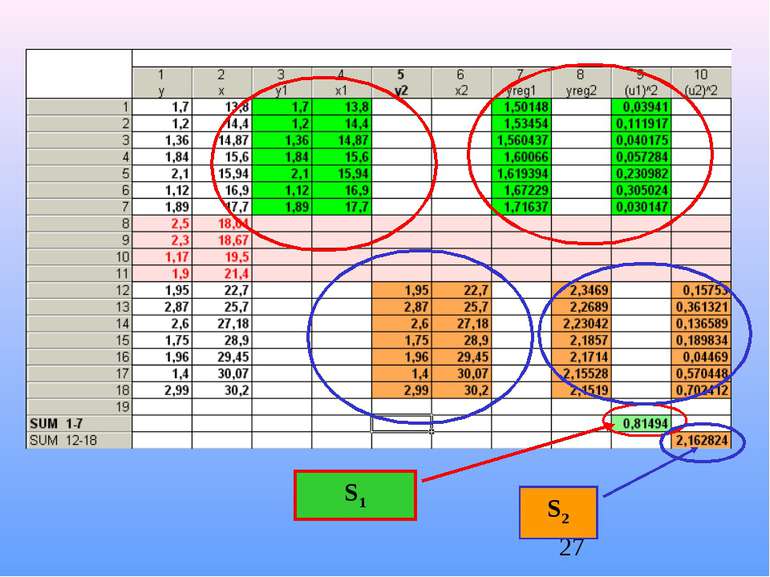
1-й крок: спостереження впорядкуємо відповідно до величини елементів вектора хi , який може викликати зміну дисперсії залишків. 2-й крок: відкинемо с спостережень усередині вектора вихідних даних, де Отримаємо дві сукупності спостережень обсягом (18-4)/2=7

3-й крок: побудуємо дві моделі на основі звичайного МНК по двох створених сукупностях спостережень

4-й крок: знайдемо суму квадратів залишків S1 і S2 по першій і другій моделях:

S1 S2

5-й крок: 5а) розрахуємо критерій який при виконанні гіпотези про гомоскедастичність буде відповідати F-розподілу з

5б) значення критерію R порівняємо з табличним значенням F-критерію при рівні довіри =0,05 і відповідних ступенях свободи: Оскільки R Fтабл., то гетероскедастичність відсутня. Отже МНК-оцінки параметрів регресійної моделі можуть застосовуватися для подальших досліджень

Завідання для самостійної роботи Лугінін О.Є. стор.148-150 Критерій μ (Зробити конспект)