Презентація на тему:
пирпр

Математику вже тому вчити треба, що вона розум у порядок приводить Геометрія - правителька всіх розумових пошуків

Девиз уроку : «Ми – успішні, ми – радісні, ми – обдаровані, ми – кмітливі»

Тема програми № 2 Перпендикулярність прямих і площин у просторі Тема уроку № 24 Розв’язування задач Математика

Мета уроку Формувати вміння застосовувати набуті знання з теми для розв’язування задач, розвивати навички працювати самостійно, активізувати розумову діяльність та виявляти свою компетентність моделювати життєві ситуації і застосовувати в різних галузях знань

Урок – подорож Математичний музей Єгипетські піраміди Білгород-Дністровська фортеця

Приклади перпендикулярів і похилих у навколишньому середовищі

Епіграф уроку : «Головне значення перпендикуляра – це його роль у техніці та у всьому нашому вжитку» Олександр Александров

Математичний музей Зала Теорії Зала Практики Теорія без практики мертва і безплідна, практика без теорії неможлива Рене Декарт

Математичний музей Зала Теорії Повторимо !

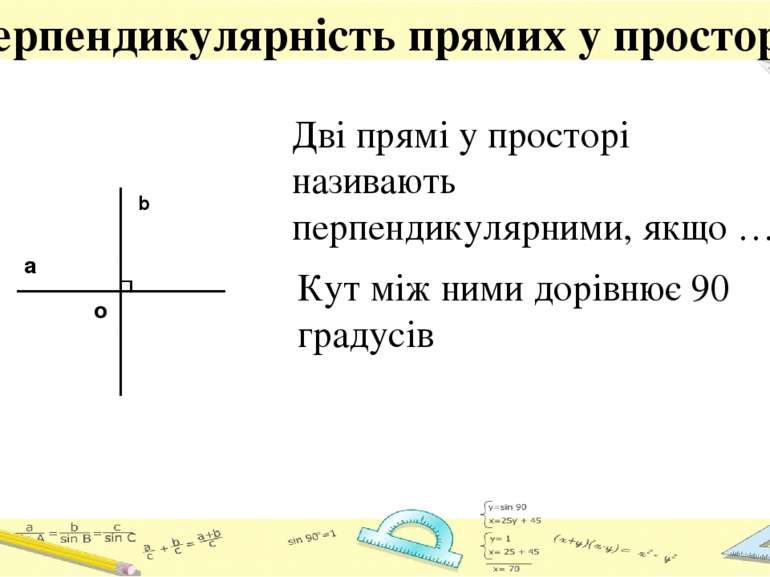
Перпендикулярність прямих у просторі Кут між ними дорівнює 90 градусів a b o Дві прямі у просторі називають перпендикулярними, якщо …

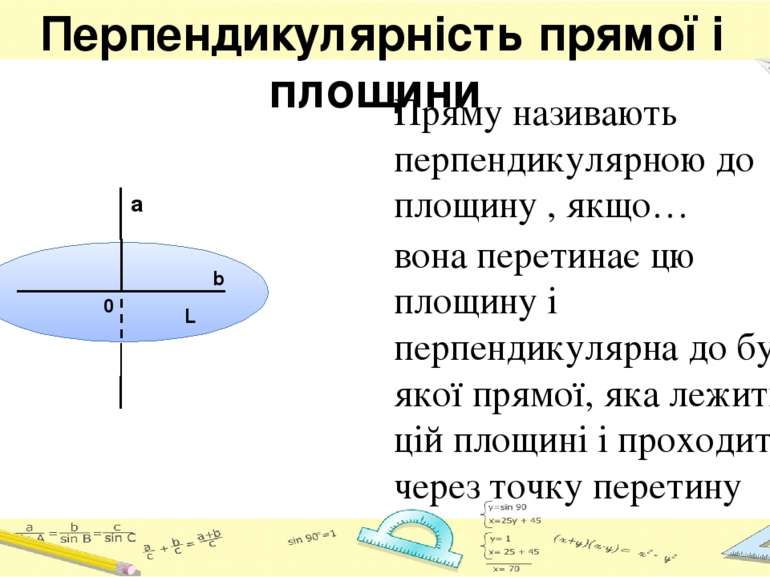
Перпендикулярність прямої і площини вона перетинає цю площину і перпендикулярна до будь-якої прямої, яка лежить у цій площині і проходить через точку перетину a b 0 L Пряму називають перпендикулярною до площину , якщо…

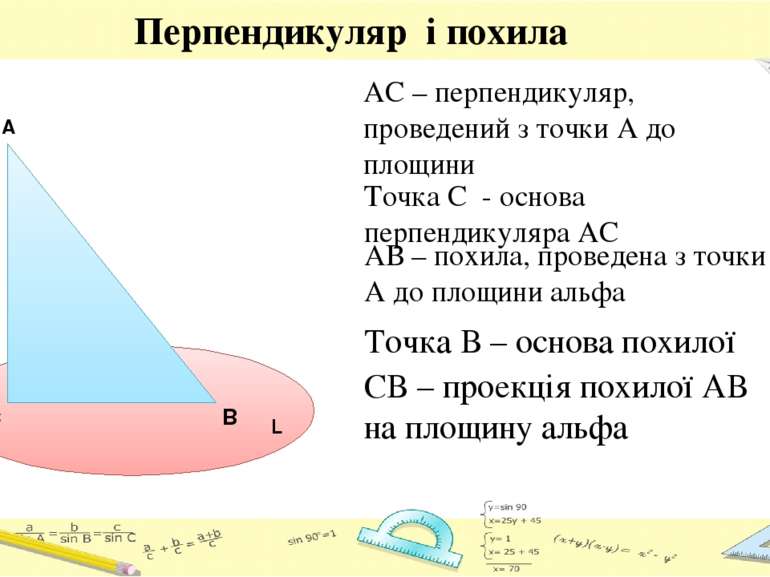
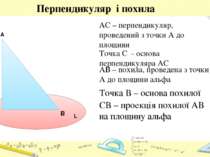
Перпендикуляр і похила АС – перпендикуляр, проведений з точки А до площини A C L B Точка С - основа перпендикуляра АС АВ – похила, проведена з точки А до площини альфа Точка В – основа похилої СВ – проекція похилої АВ на площину альфа

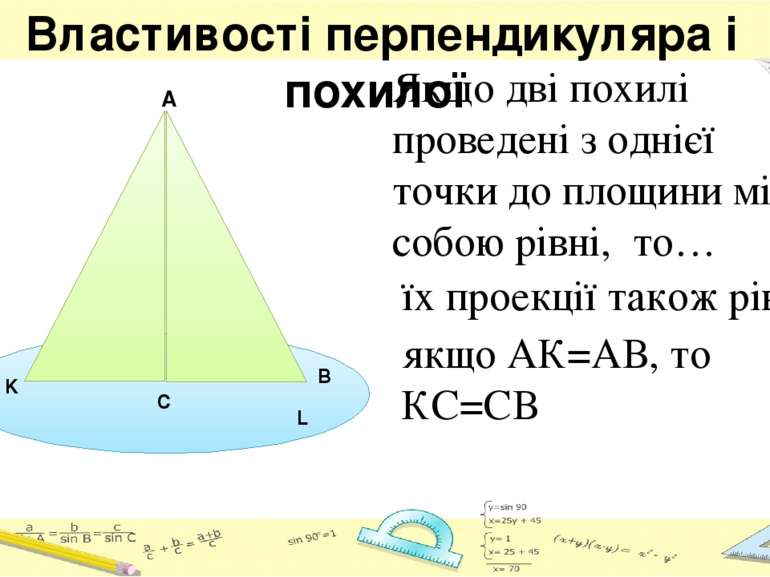
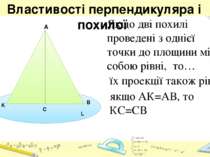
Властивості перпендикуляра і похилої Якщо дві похилі проведені з однієї точки до площини між собою рівні, то… A C L K B їх проекції також рівні: якщо АК=АВ, то КС=СВ

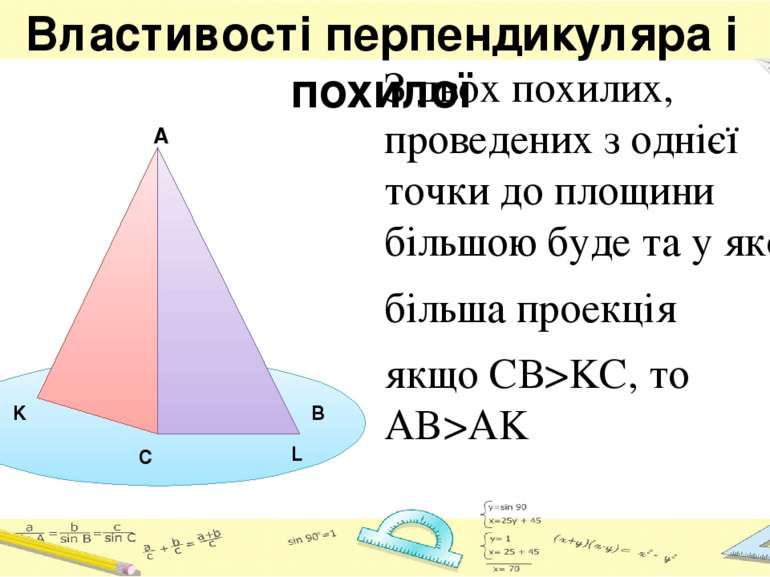
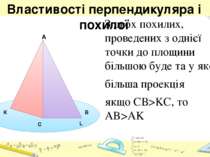
Властивості перпендикуляра і похилої З двох похилих, проведених з однієї точки до площини більшою буде та у якої… більша проекція якщо СВ>KC, то AB>AK A C L K B

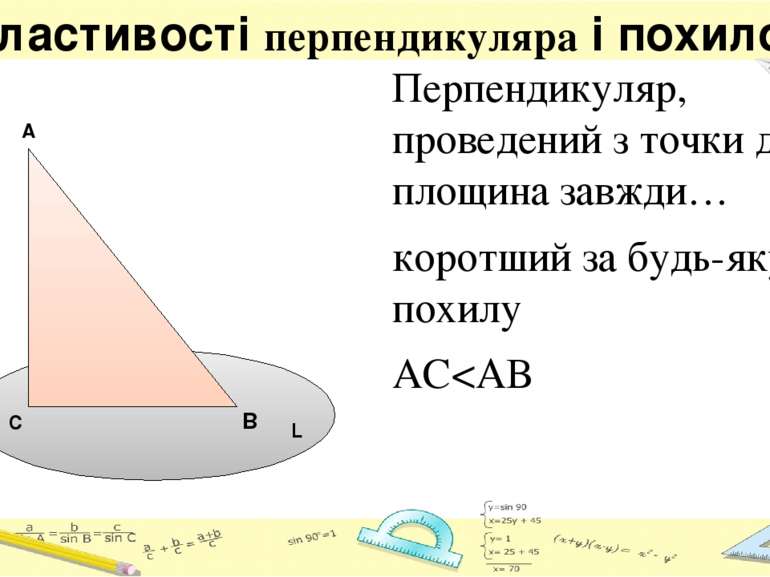
Властивості перпендикуляра і похилої Перпендикуляр, проведений з точки до площина завжди… коротший за будь-яку похилу АС

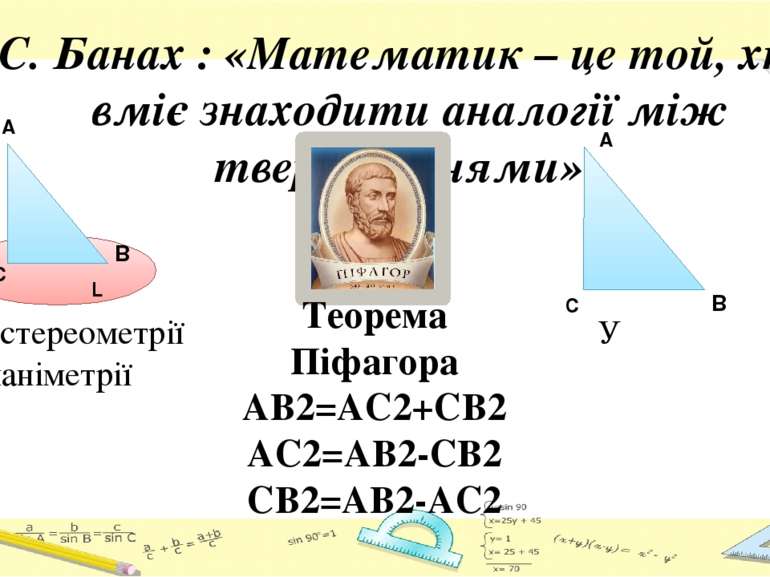
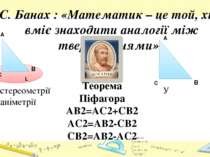
C. Банах : «Математик – це той, хто вміє знаходити аналогії між твердженнями» У стереометрії У планіметрії A C L B B C A Теорема Піфагора AB2=AC2+CB2 AC2=AB2-CB2 CB2=AB2-AC2

Математичний музей Зала Практики Розв’язування задач

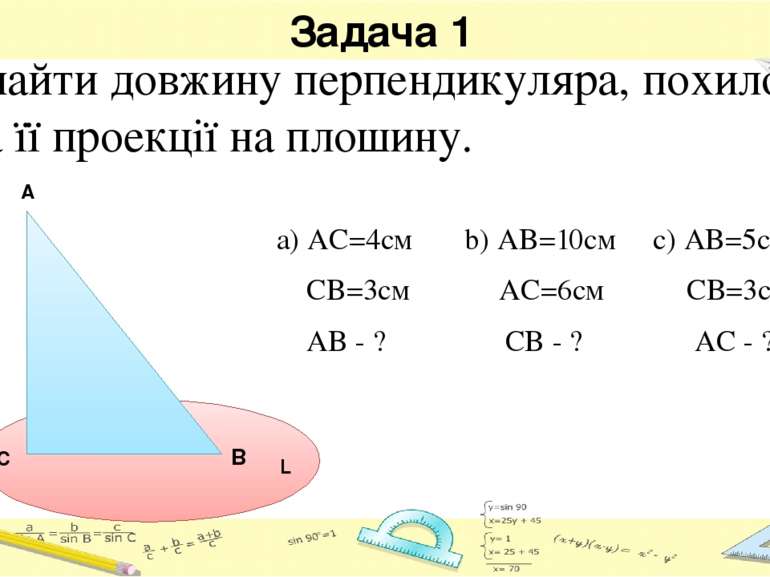
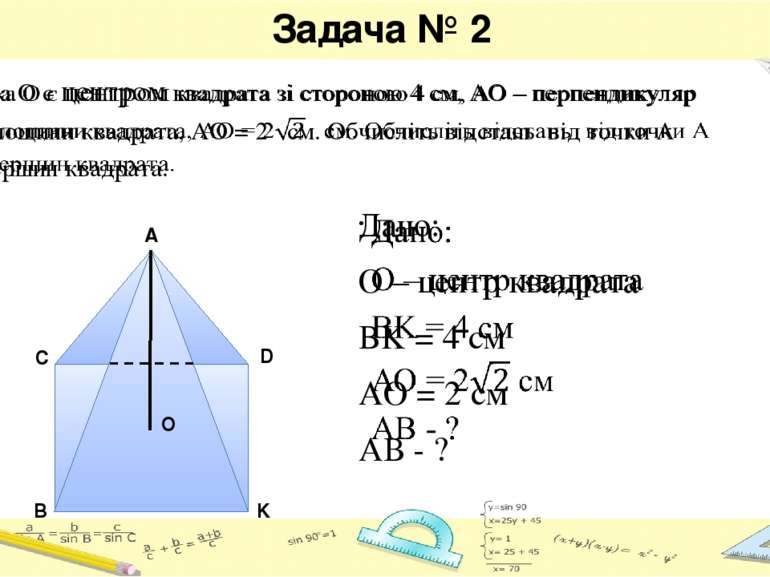
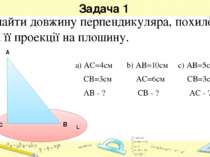
Задача 1 а) АС=4см b) AB=10см c) AB=5см СB=3см AC=6см СB=3см AB - ? CB - ? AC - ? Знайти довжину перпендикуляра, похилої та її проекції на плошину. A C L B

Задача № 2 A O D K B C

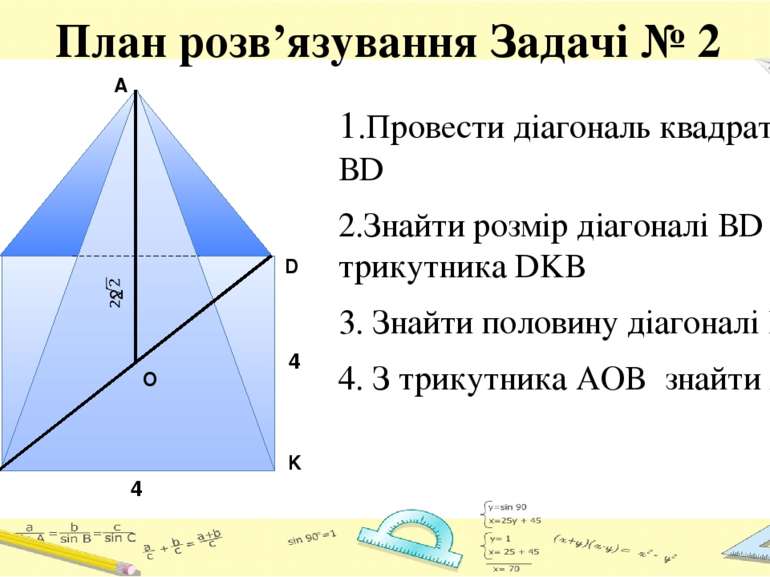
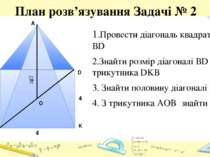
План розв’язування Задачі № 2 1.Провести діагональ квадрату ВD 2.Знайти розмір діагоналі ВD із трикутника DKB 3. Знайти половину діагоналі BD 4. З трикутника AOB знайти AB A O D K B C 4 4 4

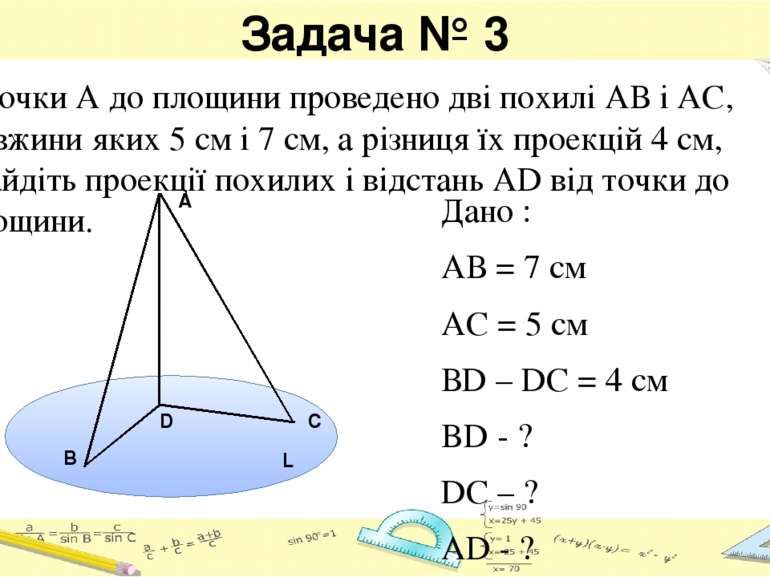
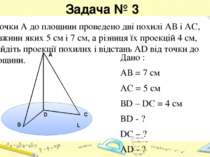
Задача № 3 Дано : АВ = 7 см АС = 5 см ВD – DC = 4 cм BD - ? DC – ? AD - ? З точки А до площини проведено дві похилі АВ і АС, довжини яких 5 см і 7 см, а різниця їх проекцій 4 см, знайдіть проекції похилих і відстань AD від точки до площини. C A L B D

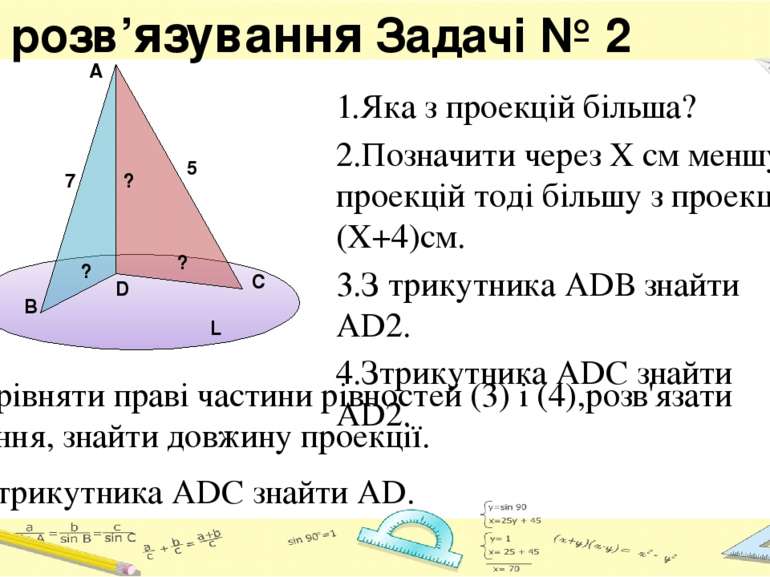
5.Зрівняти праві частини рівностей (3) і (4),розв'язати рівння, знайти довжину проекції. 6.Зтрикутника АDС знайти АD. План розв’язування Задачі № 2 1.Яка з проекцій більша? 2.Позначити через Х см меншу з проекцій тоді більшу з проекції (Х+4)см. 3.З трикутника АDВ знайти АD2. 4.Зтрикутника АDС знайти АD2. C A L B D ? ? ? 7 5

«Добре засвоєна мудрість не забувається ніколи» Піфагор

Рефлексія У мене все вийшло !!! Мені все зрозуміло !!! Потрібно розв’язати ще пару задач ! Ну хто придумав цю математику ? B C L A B C L B C L A A

«Якщо ви хочете, щоб життя посміхалося вам, подаруйте йому спочатку свій гарний настрій» Дякую вам за урок Бажаю всім успіхів та гарного настрою !