Презентація на тему:
ен

Критерії перевірки статистичних гіпотез к.е.н., ст. викладач Воляк Л.Р.

План 1. Перевірка гіпотези про рівність математичних сподівань нормальних генеральних сукупностей 2. Критерій дисперсійного аналізу 3. Критерій узгодження Пірсона

1. Перевірка гіпотези про рівність математичних сподівань нормальних генеральних сукупностей

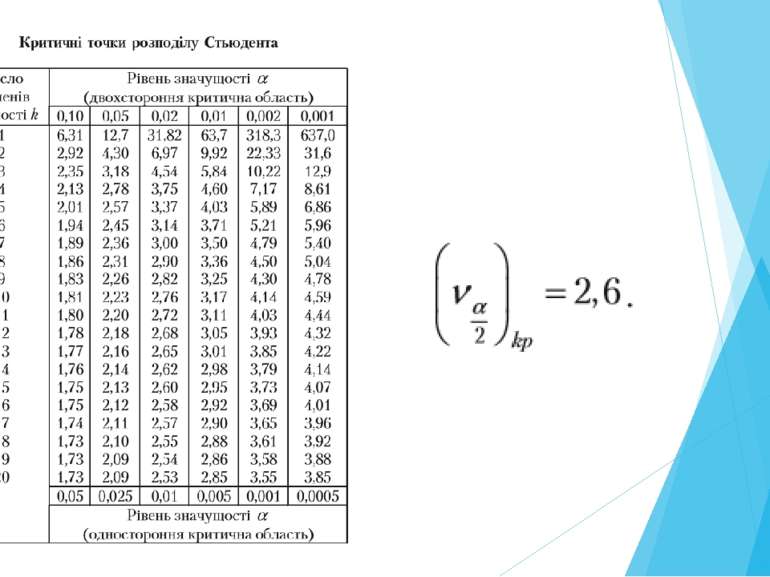
Альтернативна гіпотеза : Для перевірки гіпотези в якості статистичної характеристики (вибіркової функції) використовують функцію, яка розподілена за законом Стьюдента з степенями вільності, що дорівнюють :

2. Критерій дисперсійного аналізу Нехай є N нормально розподілених генеральних сукупностей з рівними дисперсіями та, можливо, з різними математичними сподіваннями. Із кожної сукупності робимо вибірку об’єму Тоді об’єм усієї вибірки Позначимо j варіанту випадкової величини X з і-тої сукупності ijx. Тоді середня арифметична вибірки із і-тої сукупності буде

а середня усієї вибірки буде При рівні значущості треба перевірити основну гіпотезу про рівність математичних сподівань розглядаємих сукупностей При рівності дисперсій статистична характеристика буде мати розподіл Фішера з N-1 та n-N степенів вільності. Тому в якості статистичної характеристики для перевірки цієї гіпотези використовують функцію

Критичну область у цьому випадку знаходять з урахуванням умови де fa – критичне (і табульоване) значення розподілу Фішера.

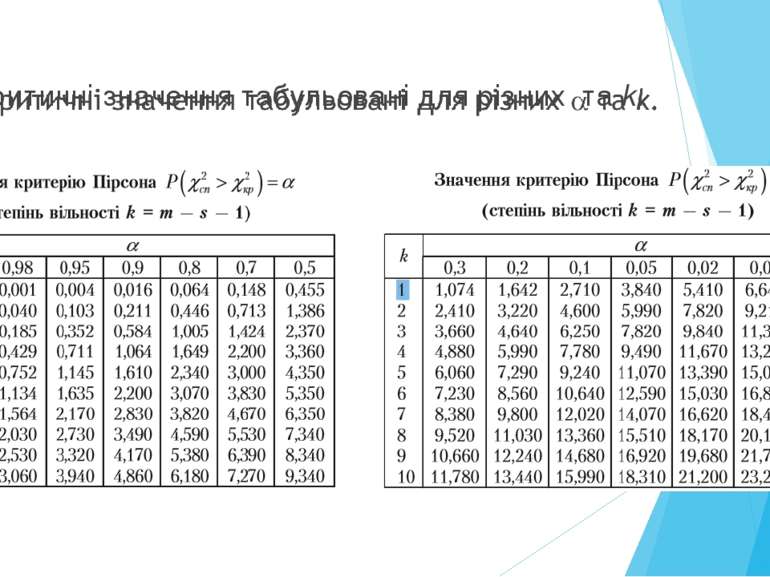
3. Критерій узгодження Пірсона Критерій узгодження Пірсона (xі-квадрат) ефективно використовують для перевірки гіпотези про розподіл генеральної сукупності, тобто що розподіл випадкової величини має певний функціональний вираз. Нехай вибірка має такий розподіл об’єму п

Для розподілу генеральної сукупності за нормальним законом степінь вільності буде де т – кількість варіант вибірки або часткових інтервалів варіант.

Правило Пірсона. Щоб при заданому рівні значущості перевірити основну гіпотезу H0 : генеральна сукупність розподілена нормально, треба обчислити теоретичні частоти для варіант вибірки; обчислити спостережене значення критерія знайти степінь вільності знайти з таблиці критичну точку порівняти зробити висновок