Презентація на тему:
Вписані й описані чотирикутники. Центральні та вписані кути. Середня лінія трикутника і трапеції.

Тема. Вписані й описані чотирикутники. Центральні та вписані кути. Середня лінія трикутника і трапеції.

Мета уроку: узагальнити й систематизувати знання учнів по вивчених темах; формувати вміння застосовувати набуті знання під час розв’язування задач; розвивати навички колективної роботи в поєднанні з самостійністю учнів; виховувати інтерес до вивчення математики, любов до рідного краю, шанування національних святинь.

ДЕВІЗ УРОКУ: КОНФУЦІЙ « Від того настрою, з яким ви вступаєте в день,  або в якусь справу залежать ваші успіхи, а можливо, і невдачі».

: Вписані й описані чотирикутники

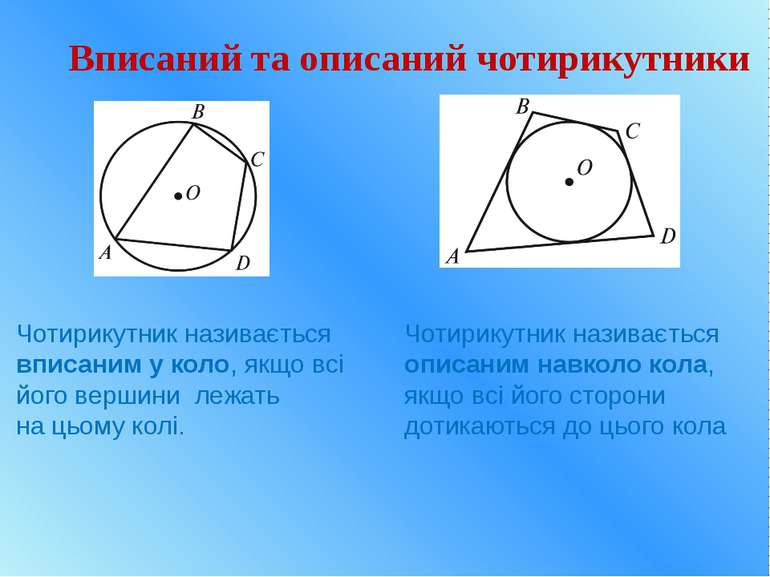
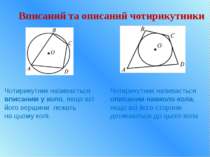
Вписаний та описаний чотирикутники Чотирикутник називається вписаним у коло, якщо всі його вершини лежать на цьому колі. Чотирикутник називається описаним навколо кола, якщо всі його сторони дотикаються до цього кола

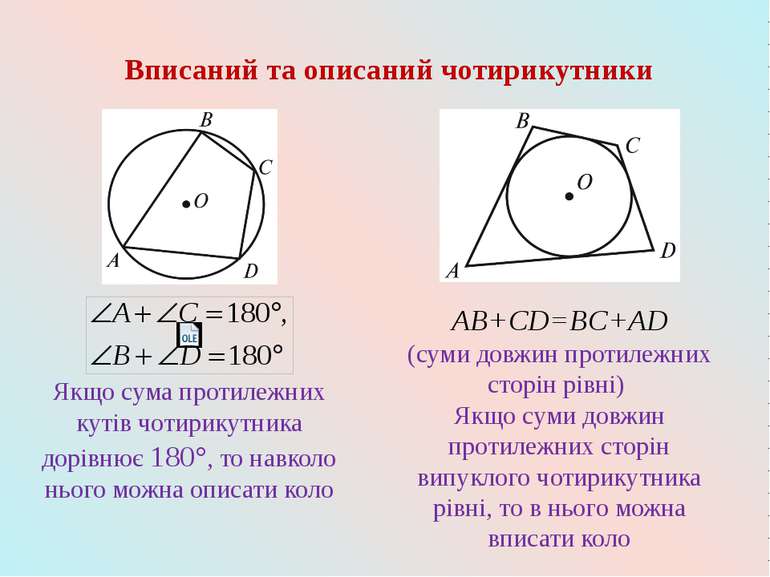
Вписаний та описаний чотирикутники AB+CD=BC+AD (суми довжин протилежних сторін рівні) Якщо суми довжин протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло Якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло

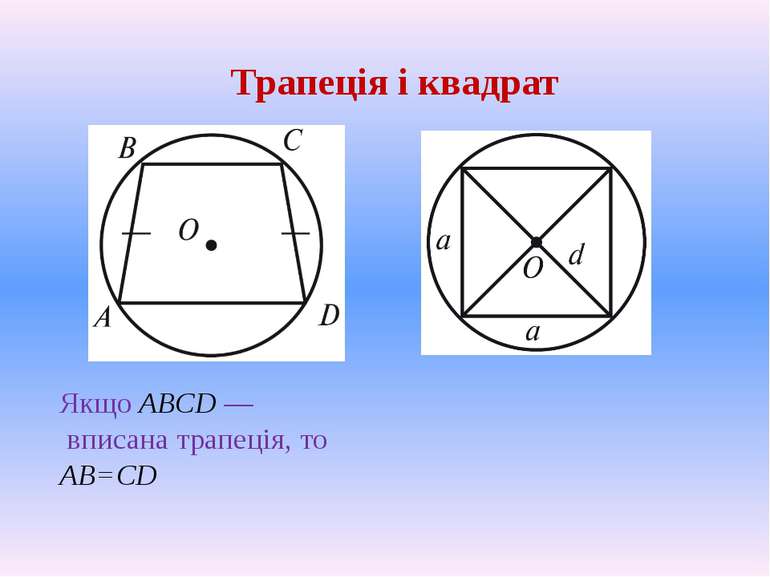
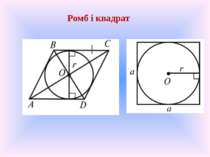
Прямокутник 1. Якщо паралелограм вписано в коло, то він прямокутник. 2. Центр кола, описаного навколо прямокутника, — точка перетину діагоналей

Трапеція і квадрат Якщо ABCD — вписана трапеція, то AB=CD

Ромб і квадрат

м е і д а т р и с а о п и с н а е 1 р а і у 2 с д а б і с е к т р и с 3 4 о л о 5 в п и с а н е 6

Чи можна описати коло, навколо чотирикутника ABCD , кути якого A, B, C, D відповідно пропорційні до чисел 3, 7, 6, 2 Задача №1 Дано:

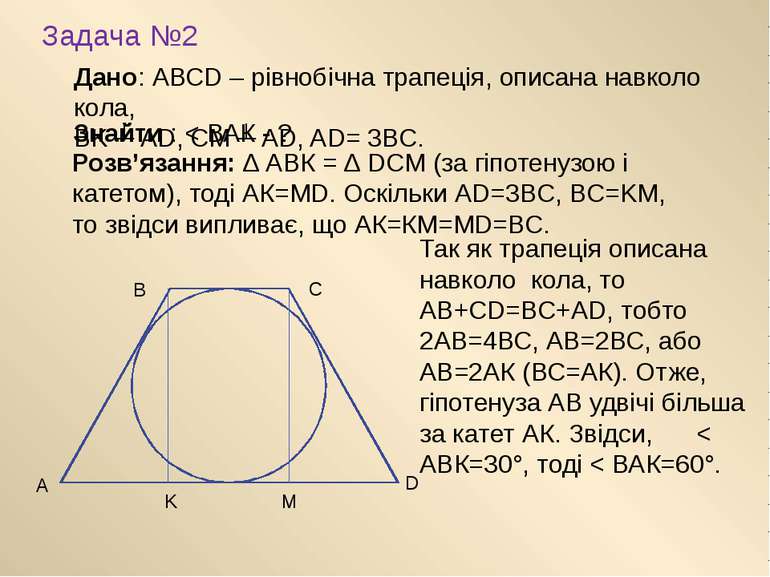
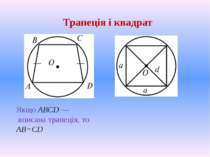
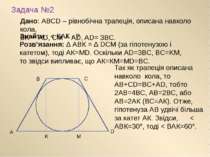
Задача №2 Дано: АВСD – рівнобічна трапеція, описана навколо кола, ВK ┴ АD, СМ ┴ AD, AD= 3BC. Так як трапеція описана навколо кола, то АВ+СD=BC+AD, тобто 2АВ=4ВС, АВ=2ВС, або АВ=2АК (ВС=АК). Отже, гіпотенуза АВ удвічі більша за катет АК. Звідси, < АВК=30°, тоді < ВАК=60°. Знайти : < ВАК - ? Розв’язання: ∆ АВК = ∆ DCM (за гіпотенузою і катетом), тоді АК=МD. Оскільки АD=3BC, BC=KM, то звідси випливає, що АК=КМ=MD=BC. А D В С K М

Вписані та центральні кути

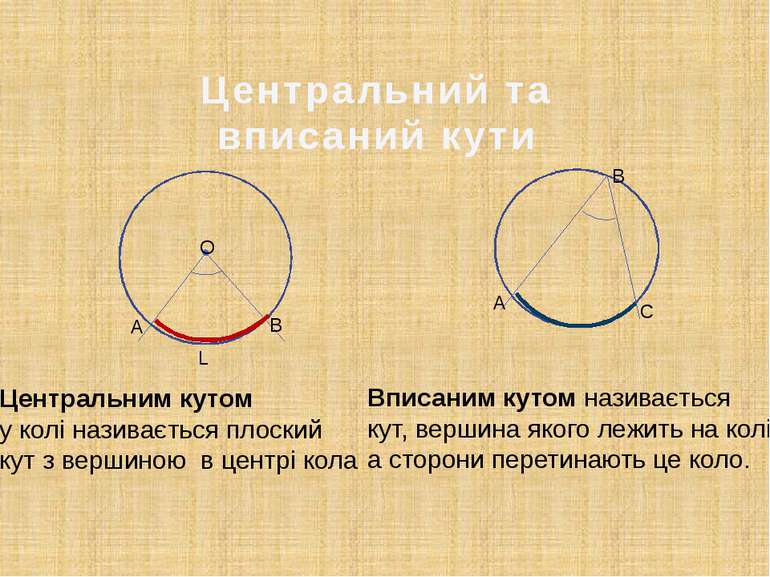
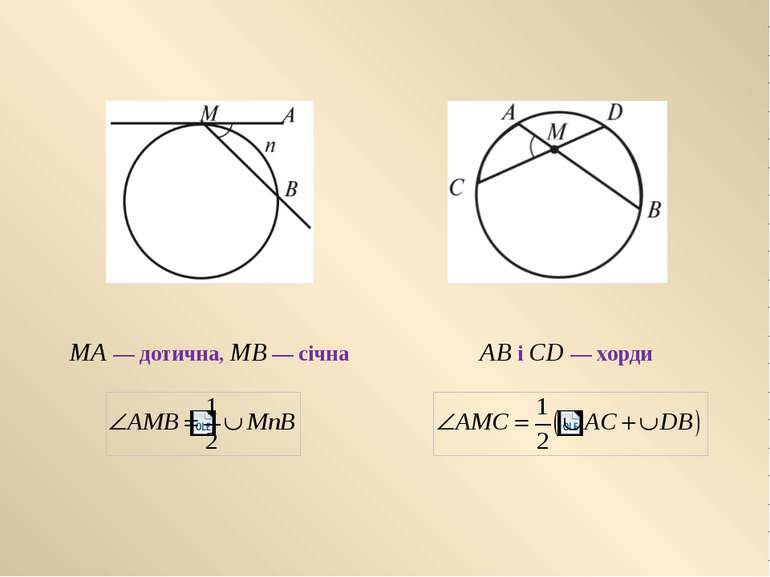
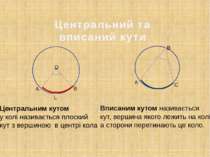
Центральний та вписаний кути Центральним кутом у колі називається плоский кут з вершиною в центрі кола Вписаним кутом називається кут, вершина якого лежить на колі, а сторони перетинають це коло. L

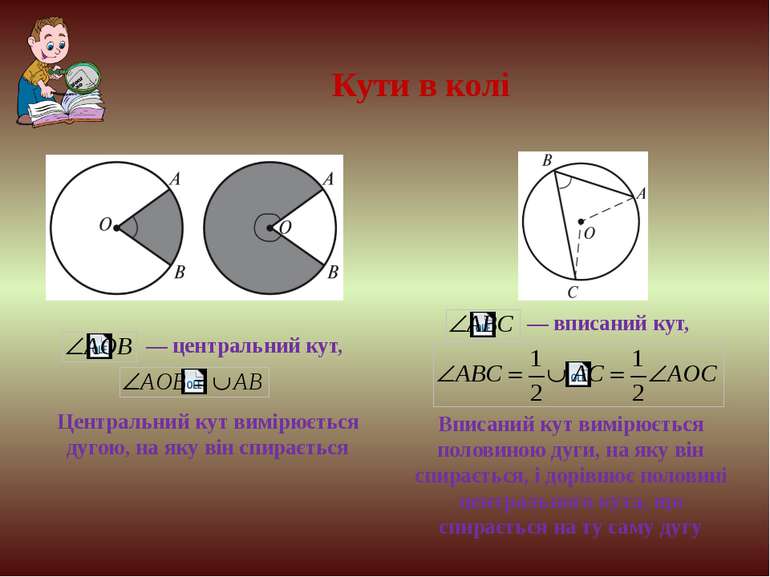
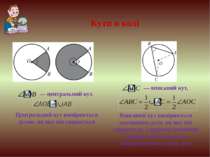
Центральний кут вимірюється дугою, на яку він спирається Кути в колі Вписаний кут вимірюється половиною дуги, на яку він спирається, і дорівнює половині центрального кута, що спирається на ту саму дугу — вписаний кут, — центральний кут,

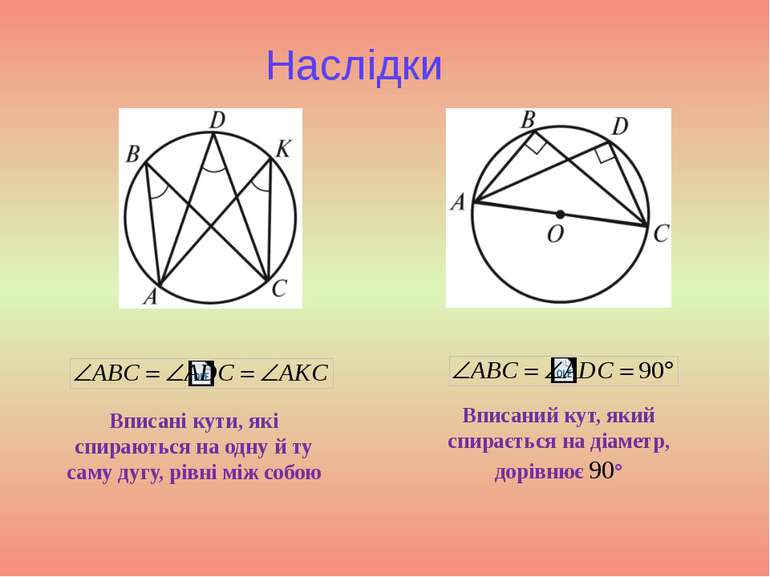
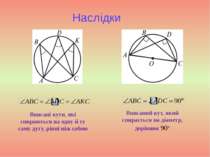
Наслідки Вписані кути, які спираються на одну й ту саму дугу, рівні між собою Вписаний кут, який спирається на діаметр, дорівнює 90°

MA — дотична, MB — січна AB і CD — хорди

Задачі за готовими рисунками Перша група Друга група Третя група к

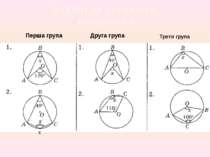
ПЕРЕВІР СЕБЕ! I – група: 1) 60° ; 2) 140° II – група: 1) 80° ; 2) 125° III – група: 1) 90° ; 2) 160°

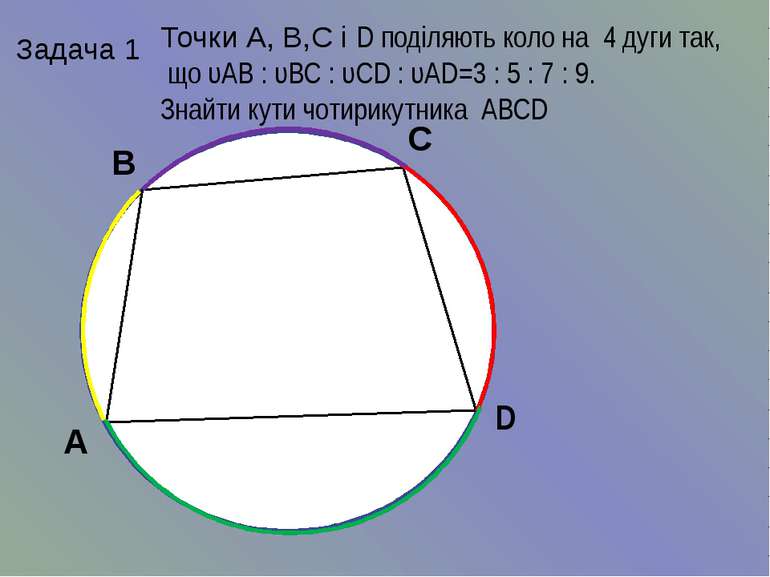
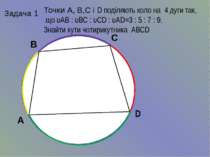
Задача 1 Точки А, В,С і D поділяють коло на 4 дуги так, що υАВ : υВС : υСD : υАD=3 : 5 : 7 : 9. Знайти кути чотирикутника АВСD А В С D

Задача 2. Довести, що гострий кут між хордою кола та дотичною до кола у кінці хорди дорівнює половині кута між радіусами проведеними до кінців хорди. Дано: АС – дотична, АВ – хорда, АО=ОВ=R. α Нехай < АОВ=α, тоді

Середня лінія трикутника і трапеції.

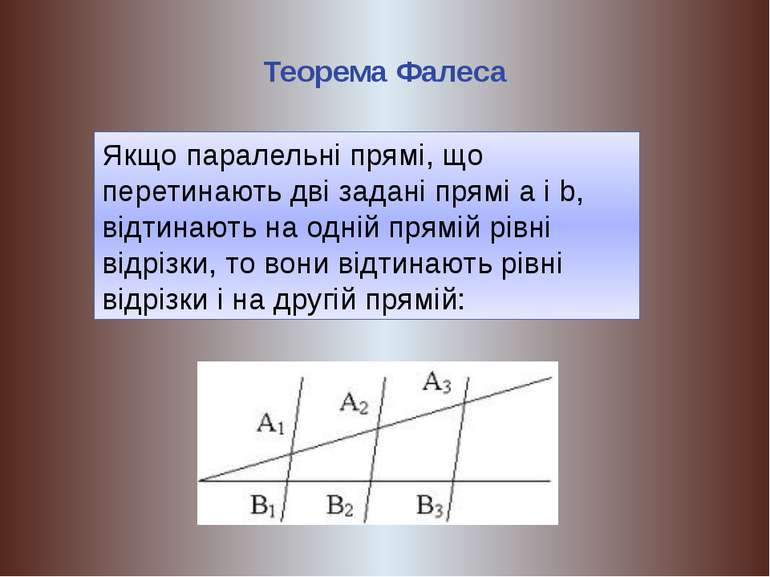
Теорема Фалеса Якщо паралельні прямі, що перетинають дві задані прямі а і b, відтинають на одній прямій рівні відрізки, то вони відтинають рівні відрізки і на другій прямій:

В одному з міст, у Мілеті, жив Фалес (близько 640—548 pp. до н. в.), якого вважають родоначальником грецької математики. Торговельні спра ви привели Фалеса до Єгипту, де він познайомився з єгипетською наукою. Геометрія зацікавила Фалеса найбільше. Решту життя вій присвятив не лише засвоєнню створеного єгиптянами в галузі геометрії, але і її розробці. Вважають, що Фалесу належить перше доведення теореми про рівність кутів при основі рівнобедреного трикутника, рівность вертикальних кутів і теореми. Історична довідка про Фалеса Мілетського

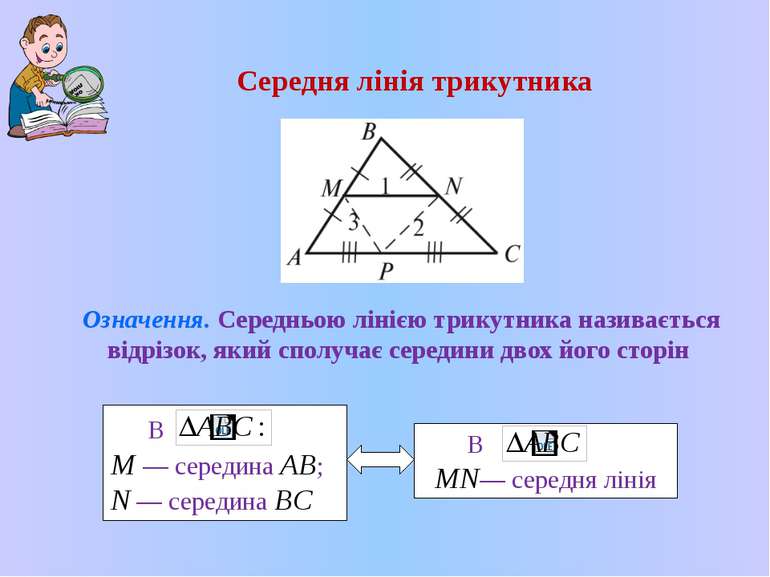
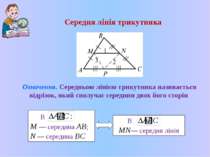
Середня лiнiя трикутника Означення. Середньою лiнiєю трикутника називається вiдрiзок, який сполучає середини двох його сторін

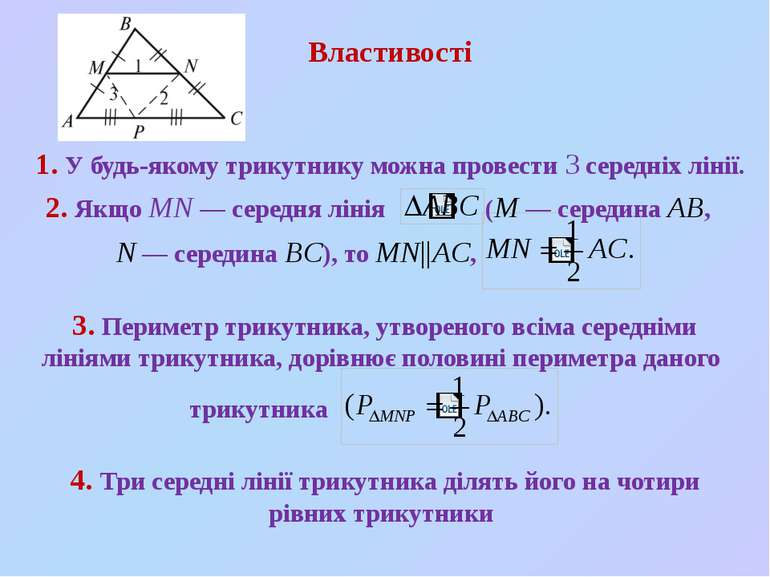
1. У будь-якому трикутнику можна провести 3 середнiх лiнiї. N — середина BC), то MN||AC, 3. Периметр трикутника, утвореного всiма середнiми лiнiями трикутника, дорiвнює половинi периметра даного 4. Три середнi лiнiї трикутника дiлять його на чотири рiвних трикутники Властивостi 2. Якщо MN — середня лiнiя (M — середина AB, трикутника

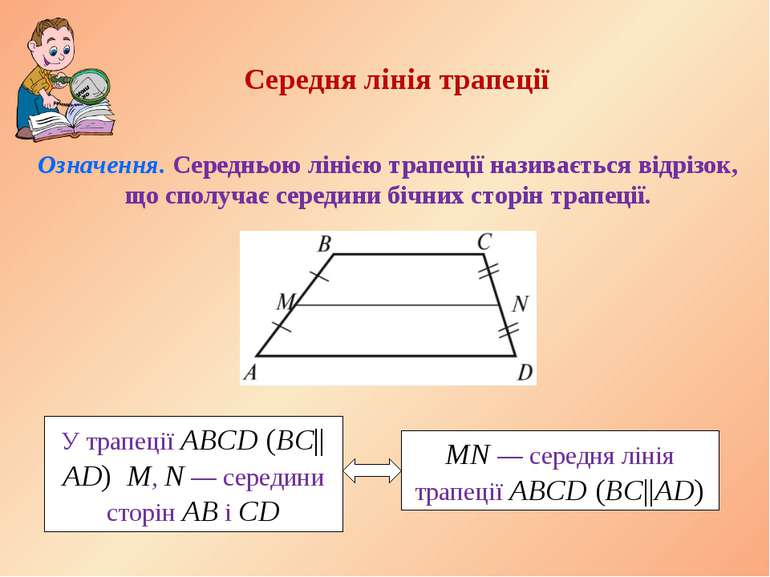
Середня лiнiя трапецiї Означення. Середньою лiнiєю трапеції називається вiдрiзок, що сполучає середини бiчних сторiн трапецiї.

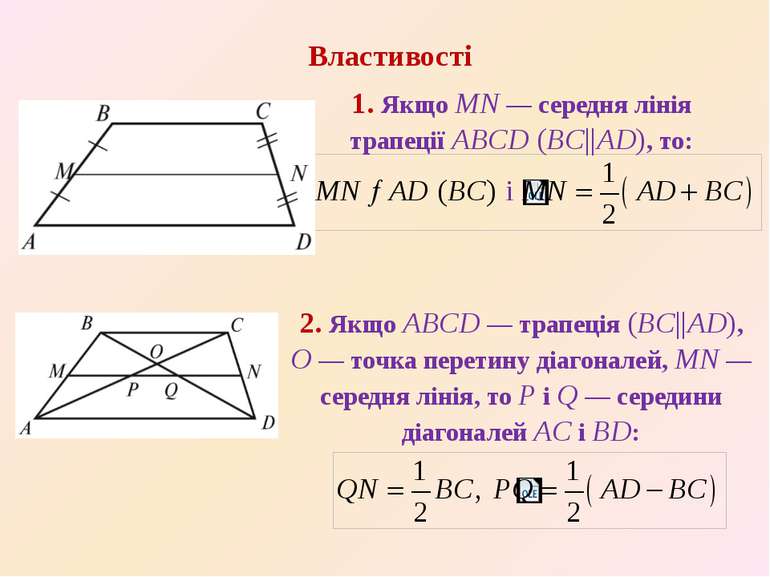
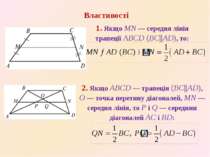
1. Якщо MN — середня лiнiя трапеції ABCD (BC||AD), то: Властивостi 2. Якщо ABCD — трапецiя (BC||AD), O — точка перетину дiагоналей, MN — середня лiнiя, то P i Q — середини дiагоналей AC i BD:

Тестові завдання: 1). MN – середня лінія трикутника АВС. Знайти довжину сторони АСIIMN, якщо MN=6см. А) 3см; Б) 18см; В) 12см; Г) 15см. 2). Середня лінія трапеції 12см, одна з основ трапеції – 8см. Знайти довжину іншої основи. А) 16см; Б) 10см; В) 8см; Г) 20см. 3). Чому дорівнює периметр рівностороннього трикутника, середня лінія якого дорівнює 4см? А) 8см; Б) 12см; В) 24см; Г) 4см. 4). Сторони трикутника дорівнюють 5см, 6см, 9см. Знайти периметр трикутника, вершинами якого є середини сторін даного трикутника. А) 10см; Б) 19см; В) 6см; Г) 20см.

ПЕРЕВІР СЕБЕ! 1). В; 2). А ; 3). В; 4). А.

Задача. У рівнобічній трапеції діагональ ділить гострий кут навпіл. Периметр трапеції дорівнює 132 см. Знайти середню лінію трапеції, якщо основи відносяться як 2:5. А В С Дано: АВ=СD, < 1= < 2 (АС - бісектриса), ВС: АD= 2:5, ВС=2х, АD= 5х, P= 132 см. Розв’язання:

Дякую за урок!