Презентація на тему:
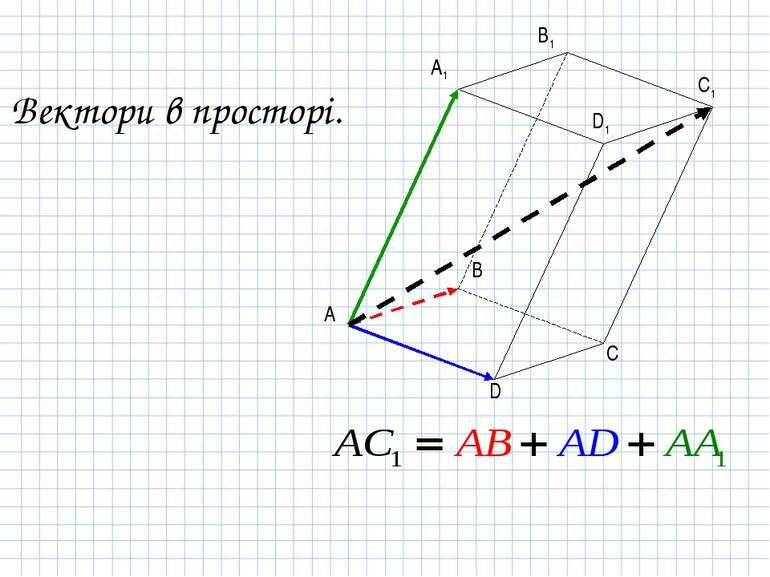
Вектори в просторі.

Вектори в просторі. A B C D A1 B1 C1 D1

Як і на площині, в просторі вектор визначається як направлений відрізок: A B Точка А – початок вектора, В – кінець вектора. Записують: або . a Довільну точку в просторі ми також можемо вважати вектором, у якого початок співпадає з кінцевою точкою. Такий вектор називається нульовим і позначається: . або A Довжина відрізка, що зображає вектор, називається модулем (або абсолютною величиною) вектора, тобто Відповідно, що I. Визначення вектора. Основні поняття, звязані з векторами. A B Вектори і являються протилежними. Очевидно, що:

Два вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих: a b c Колінеарні вектори, в свою чергу, бувають однаково направленими (або співнаправленими) і протилежно направленими. В нашому випадку: Позначення колінеарних векторів: – співнаправлені вектори, , – протилежно направлені вектори. m n Два вектори називаються рівними, якщо: 1) вони співнаправлені; і 2) їх модулі рівні, тобто

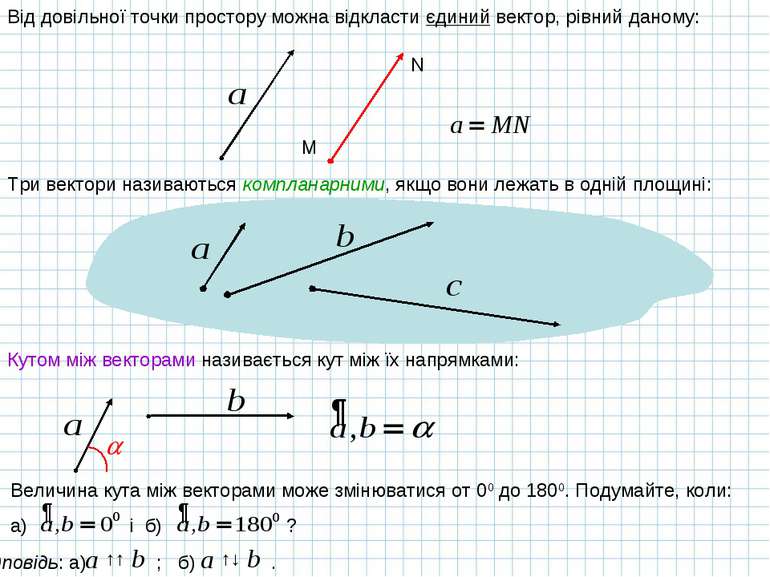
Від довільної точки простору можна відкласти єдиний вектор, рівний даному: M N Три вектори називаються компланарними, якщо вони лежать в одній площині: Кутом між векторами називається кут між їх напрямками:

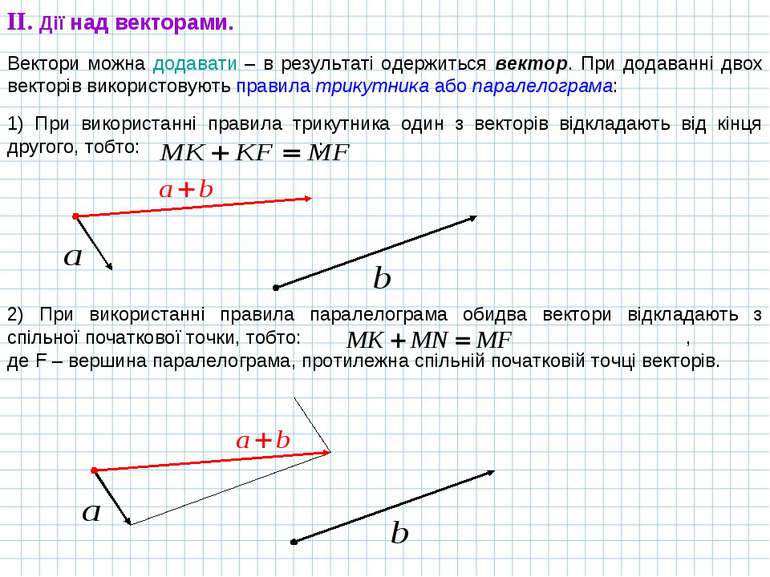
II. Дії над векторами. Вектори можна додавати – в результаті одержиться вектор. При додаванні двох векторів використовують правила трикутника або паралелограма: 1) При використанні правила трикутника один з векторів відкладають від кінця другого, тобто: : 2) При використанні правила паралелограма обидва вектори відкладають з спільної початкової точки, тобто: , де F – вершина паралелограма, протилежна спільній початковій точці векторів.

При додаванні трьох і більше векторів використовують правило многокутника: Звернемо увагу, що при додаванні співнаправлених векторів одержується вектор, співнаправлений с даними і його модуль рівний сумі модулів векторів, які додаються: При додаванні протилежно направлених векторів одержується вектор, співнаправлений з вектором, який має більшу довжину і його модуль рівний … (подумайте, чому?):

Також можна знайти різницю двох векторів – в результаті одержиться вектор. При відніманні двох векторів використовують видозмінене правило трикутника – спочатку обидва вектори будуються з спільною початковою точкою, потім зєднуються кінці цих векторів з вибором напряму до «зменшуваного» вектора: Або: так як , то можна спочатку побудувати вектор, протилежний вектору , а потім обидва вектори додати по правилу трикутника. –

Додавання векторів, як ідодавання чисел підпорядковується законам: Слідуюча дія з векторами –множення вектора на число k. В результаті цієї дії одержується вектор, причому: якщо k>0, то і ; якщо k

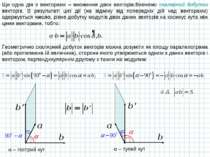
Ще одна дія з векторами – множення двох векторів.Вивчемо скалярний добуток векторів. В результаті цієї дії (на відміну від попередніх дій над векторами) одержується число, рівне добутку модулів двох даних векторів на косинус кута між цими векторами, тобто: Геометрично скалярний добуток векторів можна розуміти як площу паралелограма (або протилежна їй величина), сторони якого утворюються одним з даних векторів і вектором, перпендикулярним другому з таким же модулем: – гострий кут – тупий кут

Тепер розглянемо всі ці поняття і дії з точки зору координатного простору. Згадаємо, що люба точка простору задається трьома координатами А(x;y;z). A(x1;y1;z1) B(x2;y2;z2) Якщо прийняти вектор за паралельне перенесення початкової точки A(x1;y1;z1) в кінечну точку B(x2;y2;z2), то координати вектора показують: на скільки змінюються відповідні координати початкової точки при паралельному перенесенні в кінечну, тобто: Так як, модуль вектора рівний довжині відрізка, що його зображає , то: III. Координати вектора. Дії над векторами в координатах.

Для додавання двох векторів, заданих координатами, потрібно просто додати їх відповідні координати, тобто: При відніманні векторів, заданих координатами, потрібно знайти різницю їх відповідних координат, тобто: Множення вектора, заданого координатами, на число виконується так: Скалярний добуток двох векторів, заданих координатами, рівний сумі добутків відповідних координат, тобто: Умовою колінеарності двох векторів, заданих координатами, буде пропорціональність їх відповідних координат: Самостійно розберіться, коли і .

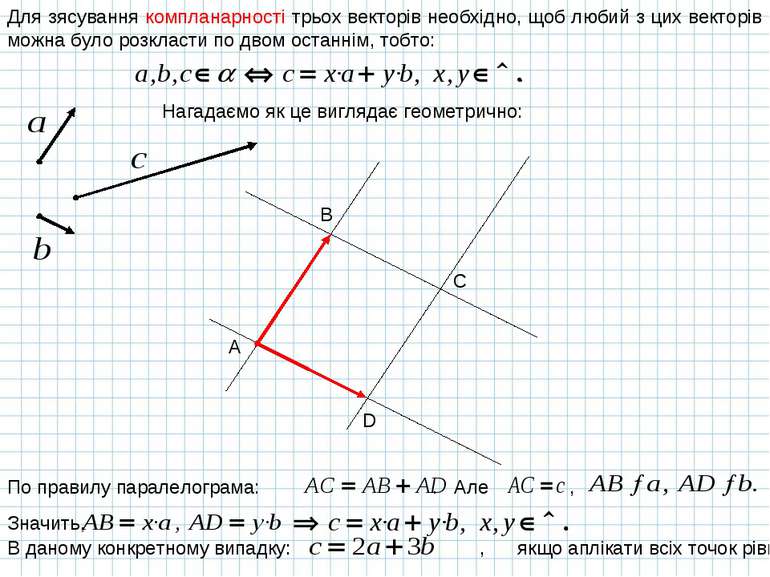
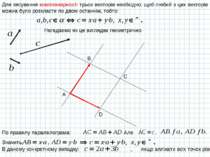
Для зясування компланарності трьох векторів необхідно, щоб любий з цих векторів можна було розкласти по двом останнім, тобто: A B C D Нагадаємо як це виглядає геометрично:

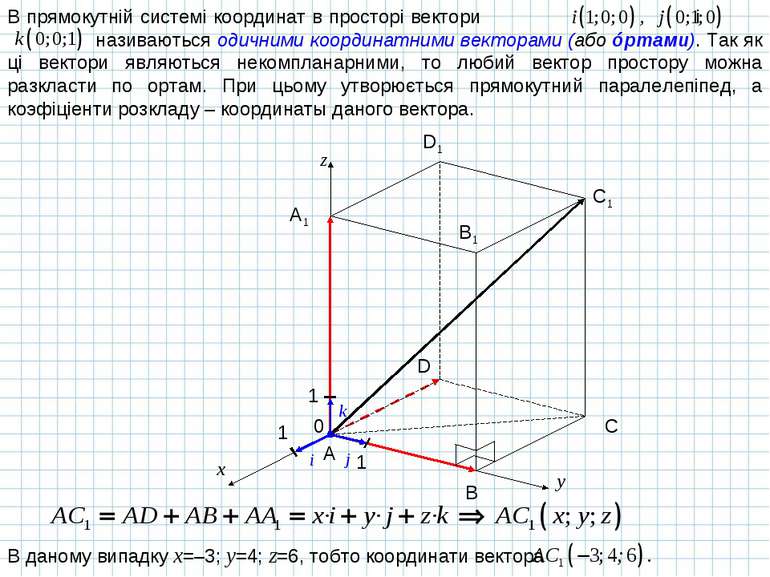
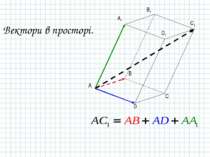
В прямокутній системі координат в просторі вектори і називаються одичними координатними векторами (або óртами). Так як ці вектори являються некомпланарними, то любий вектор простору можна разкласти по ортам. При цьому утворюється прямокутний паралелепіпед, а коэфіціенти розкладу – координаты даного вектора. x y z A B C D A1 B1 C1 D1 0 1 1 1

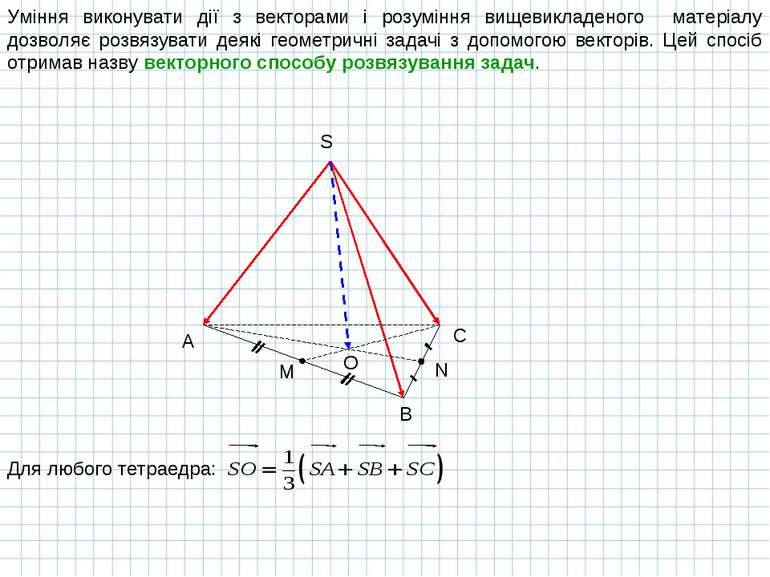
Уміння виконувати дії з векторами і розуміння вищевикладеного матеріалу дозволяє розвязувати деякі геометричні задачі з допомогою векторів. Цей спосіб отримав назву векторного способу розвязування задач. A B C M N S O