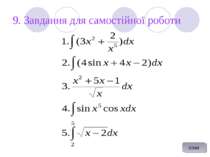Презентація на тему:
Математична обробка
Завантажити презентацію
Математична обробка
Завантажити презентаціюПрезентація по слайдам:
“Медична і біологічна фізика” під загальною редакцією член-кореспондента АПН України професора О.В.Чалого том 1
Роботу виконав учень 11-Б класу ІV групи УМЛ НМУ ім. О.О.Богомольця Михальчук Дмитрій під керівництвом Лялько Віри Іванівни
ЗМІСТ Розділ 1. Математична обробка медико-біологічної інформації 1.1.Елементи диференціального числення. 1.1.1. Похідна та диференціал функції. 1.1.2. Основні правила диференціювання. 1.1.3. Таблиця похідних основних елементарних функцій. 1.1.4. Правило диференціювання складної функції. 1.1.5. Похідні вищого порядку. 1.1.6.Дослідження функцій на монотонність. Максимуми та мінімуми. 1.1.7. Випуклість та увігнутість графіка функції. Точки перегину. 1.1.8. Побудова графіків функцій. 1.1.9. Практичне заняття 1.1.10.Завдання для самостійної роботи 1.1.11.Питання по матеріалу 1.2.Функції декількох змінних 1.1.1.Частинні похідні і диференціали функції декількох змінних. 1.2.2.Повний диференціал . 1.2.3.Застосування диференціала функції для обчислення похибок. 1.2.4.Практичне заняття. 1.2.5.Завдання для самостійної роботи. 1.2.6.Питання по матеріалу.
1.3. Елементи інтегрального числення. 1.3.1.Первісна. Невизначений інтеграл. 1.3.2.Властивості невизначеного інтеграла. 1.3.3.Таблиця найпростіших інтегралів. 1.3.4.Оновні методи інтегрування. 1.3.5.Визначений інтеграл. 1.3.6.Властивості визначеного інтеграла. 1.3.7.Формула Ньютона-Лейбніца. 1.3.8.Практичне заняття. 1.3.9.Завдання для самостійної роботи. 1.3.10.Запитання по матеріалу. 1.4.Елементи теорії звичайних диференціальних рівнянь. 1.4.1.Поняття про диференціальні рівняння. 1.4.2.Лінійні диференціальні рівняння. 1.4.3.Диференціальні рівняння зі змінними, що розділяються. 1.4.4.Лінійні диференціальні рівняння другого порядку з постійними коефіцієнтами. 1.4.5.Практичне заняття. 1.4.6.Завдання для самостійної роботи. 1.4.7.Запитання по матеріалу.
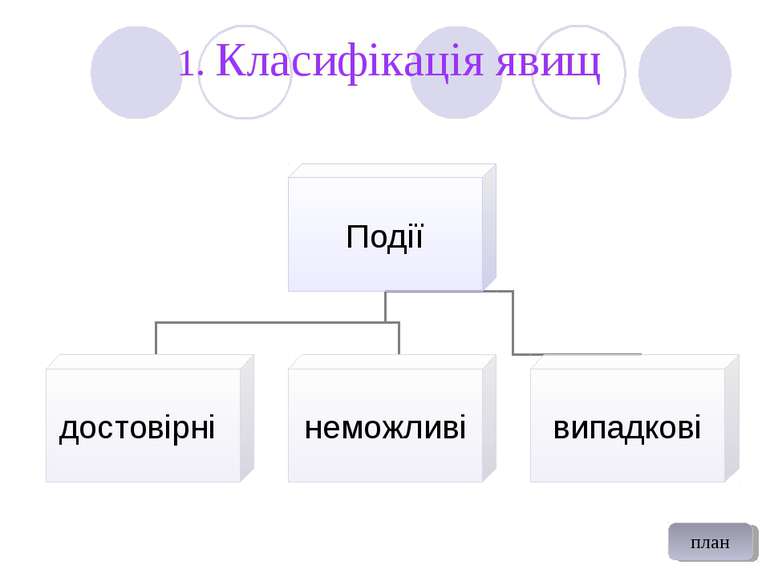
1.5. Особливості теорії ймовірностей та математичної статистики. 1.5.1. Класифікація явищ . Частота та ймовірність події. 1.5.2. Теорема додавання ймовірностей. 1.5.3. Теорема множення ймовірностей. 1.5.4. Формула повної ймовірності . Формули Байєса. 1.5.5. Повторні випробування . Формула Бернуллі . 1.5.6. Випадкова величина , дискретні та неперервні випадкові величини. 1.5.7. Інтегральна та диференціальна функції розподілу. 1.5.8. Основні кількісні характеристики розподілу випадкових величин. 1.5.9. Основні закони розподілу випадкових величин. 1.5.10. Кореляційна залежність. 1.5.11.Практичне заняття. 1.5.12.Завдання для самостійної роботи. 1.5.13.Запитання по матеріалу. Томас Байєс Дені Пуассон Карл Фрідріх П'єр – Сімон Ланлас
“ ...В наступні роки я не міг пробачити собі той недолік витримки, який не дозволив мені подолати математику, щоб розібратися в її великих керівних принципах. У людей, що засвоїли ці принципи, на один орган почуттів більше, ніж у звичайних смертних.” Чарльз Дарвін
1.Похідна та диференціал функції Похідною у’ від функції у = f (x) по аргументу х називається границя відношення приросту функції Δу до приросту аргументу Δх за умови, що приріст аргументу нескінченно малий Δх →0 план
Диференціал dy – це лінійна частина приросту функції, оскільки добуток ∞( Δх) Δх – величина нелінійна відносно Δх.
Звідси: тобто диференціал незалежної змінної дорівнює її приросту. Остаточно маємо: диференціал функції дорівнює добутку похідної функції на диференціал незалежної змінної:
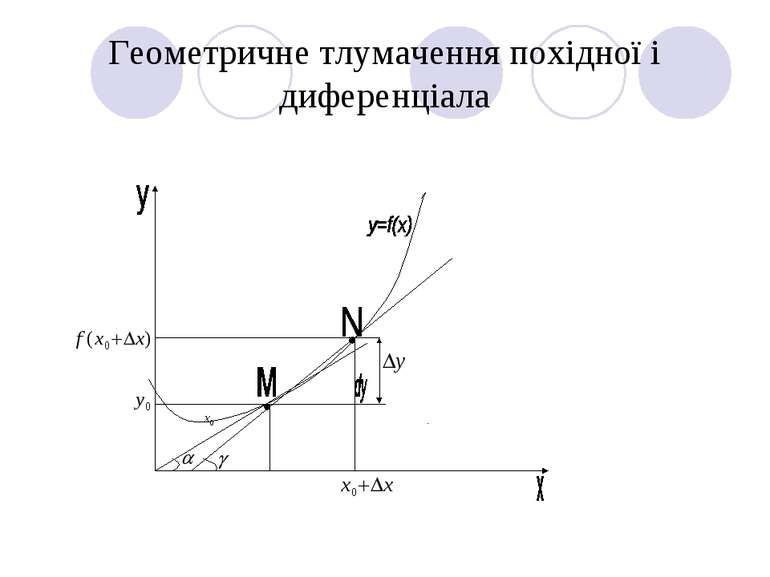
Геометричне тлумачення похідної тісно пов’язане з поняттям дотичної Якщо точка N прямує до М, то січна МN займе граничне положення, для якого в при . Таким чином, значення похідної у точці х0 визначає кутовий коефіцієнт дотичної, проведеної до графіка функції у = f (x) у точці М (х0, у0), тобто
Фізичне тлумачення похідної і диференціала У кожній точці, де функція у = f (x) диференційована, похідна y’ = f’(x0) являє собою швидкість зміни функції у цій точці відносно аргументу х. Заміна приросту функції її диференціалом дозволяє вважати процес зміни функції лінійним відносно достатньо малих змін аргументу.
2.Основні правила диференціювання 1) похідна суми двох функцій дорівнює сумі похідних цих функцій: 2) похідна добутку визначається за формулою: 3) Похідна частки: 4) Постійний множник можна вивести за знак похідної: план
4. Правило диференціювання складної функції Якщо у = f (u), а u = b (x), тобто у = f [b (x)] – складна функція і функції y(u) та u(x) – диференційовані, то складна функція y = f [b (x)] також диференційована, причому план
Це правило поширюється на ланцюжок із будь-якого числа диференційованих функцій. Наприклад, якщо , то
5. Похідні вищого порядку Похідною другого порядку чи другою похідною функції називається похідна від її першої похідної: Визначення (математичне) другої похідної в точці х = х0 план
Монотонні функції Функції, в яких перша похідна на деякому проміжку не змінює знак, називаються монотонними на цьому проміжку. Монотонні функції часто зустрічаються у різних дослідженнях. Наприклад, освітленість – монотонно спадна функція відстані від джерела світла.
Максимуми та мінімуми функцій Функція f (x) має у точці х0 максимум (мінімум), якщо існує такий окіл цієї точки (х0 – δ, х0 + δ), що для всіх х із цього околу виконується нерівність: f (x) < f (x0) (f (x) > f (x0)). Максимум чи мінімум функції називається екстремумом функції.
Необхідна умова існування екстремуму Якщо диференційована в деякому інтервалі (a; b) функція має в точці х0 є (a; b) екстремум, то її похідна в цій точці дорівнює нулю: f’ (x0) = 0. Точки, в яких похідна перетворюється в нуль, називаються критичними.
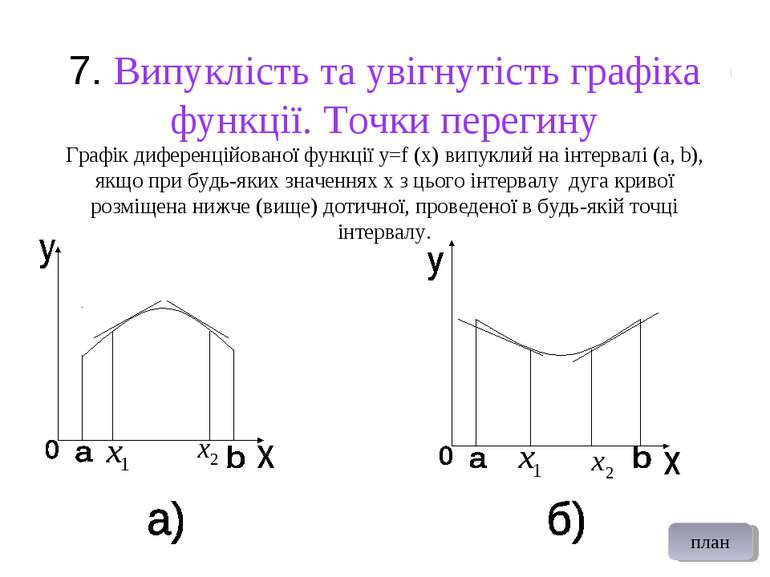
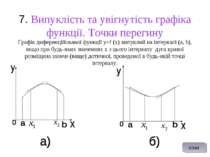
7. Випуклість та увігнутість графіка функції. Точки перегину Графік диференційованої функції y=f (x) випуклий на інтервалі (a, b), якщо при будь-яких значеннях х з цього інтервалу дуга кривої розміщена нижче (вище) дотичної, проведеної в будь-якій точці інтервалу. план
Якщо при будь-яких значеннях х в інтервалі a і b дуга кривої розміщена нижче (вище) дотичної, проведеної в будь-якій точці інтервалу (мал. а - випуклий, мал. б - увігнутий).
8. Побудова графіків функцій Повне дослідження функції проводиться за схемою: знаходять області визначення функції, точки розриву, множину значень функції; знаходять асимптоти графіка; досліджують функцію на парність, непарність, періодичність; досліджують функцію на монотонність і знаходять її; визначають напрямок випуклості графіка, точки перегину; знаходять точки перетину з осями координат; будують графік. план
9. Практичне заняття ПРИКЛАД Знайти похідну функції Розв'язок : запишемо функцію у вигляді і використаємо правило знаходження похідної степеневої функції план
Запитання по матеріалу Що називається похідною у’ від функції у = f (x) по аргументу х? Як інакше можна розтлумачити формулу f (x + +Δx) ≈ f (x) + f’ (x) dx? Назвіть основні правила диференціювання? Що таке похідна другого порядку? Що таке монотонні функції? план
1. Частинні похідні і диференціали функції декількох змінних Поняття функції однієї змінної не охоплює всі залежності , що існують у природі. У багатьох прикладних задачах доводиться мати справу з функціями декількох змінних y=f (x, t) u=f (x, y, z, t,). Наприклад, чисельність популяції бактерій є функцією часу, температури і концентрації поживних речовин. Зменшення кров'яного тиску залежить від кількості введеного лікарського препарату, маси тіла пацієнта, часу тощо. план
Для спрощення розглядатимемо функцію двох незалежних змінних z=f (x, t). Способи задання функції двох змінних, які у випадку однієї змінної, можуть бути різними. Ми найчастіше будемо використовувати аналітичний спосіб задання. Областю визначення функції у цьому випадку вважається множина усіх точок площини, для яких формула має зміст. Зафіксуємо t = , тоді z – функція лише однієї змінної х. Її приріст ∆z дорівнює: Утворимо відношення та знайдемо границю цього відношення при Ця величина називається частинною похідною від функції z=f (x, t) за змінною х у точці
2. Повний диференціал Розглянемо u= f (x, y, z) – функцію трьох незалежних змінних, яка є визначеною і диференційованою у деякому інтервалі. Головна, лінійна відносно ∆x, ∆y, ∆z, частина приросту функції називається повним диференціалом du функції трьох змінних : план
3. Застосування диференціала функції для обчислення похибок Для знаходження похибок використовують метод заміни простору функції її диференціалом. Точність вимірювання характеризується похибкою. Абсолютна похибка – це різниця між вимірюваним та точним значенням величини (i = 1, 2, …n). Відносна похибка – відношення абсолютної похибки до точного (істинного) значення вимірюваної величини: план
4. Практичне заняття Приклад. Знайти частинні похідні функції: Розв'язок: розглядаючи у як постійну величину, знайдемо частинну похідну функцію z (x, y) за зміною х Аналогічно знайдемо частинну похідну за змінною у, при цьому змінну х вважатимемо константою план
6.Запитання по матеріалу З якою метою у фізику введене поняття “диференціал функції декількох змінних”? Що називається частинною похідною від функції z = f (x, t)? Записати формулу повного диференціала функції трьох змінних. Яким чином визначають похибку вимірювання? Що називається відносною похибкою? план
1.Первісна. Невизначений інтеграл Потрібно вміти знаходити функцію f (x) за її похідною f‘ (x), тобто виконати дію, обернену до диференціювання. Наприклад: Знайти закон, за яким змінювалась швидкість v (t), якщо залежність прискорення від часу a (t) відома. Шуканою функцією буде така v (t), для якої виконується формула Знайти закон руху матеріальної точки за відомою залежністю швидкості від часу план
Функція F (x) називається первісною для функції f (x), якщо F (x) має свою похідною функцію: Теорема про існування первісної: Кожна неперервна функція має нескінченну кількість первісних, які відрізняються одна від одної на постійний додаток. Визначення: сукупність усіх первісних F (x) + C для даної функції f (x) називається невизначеним інтегралом функції f (x). Згідно з означенням:
2. Властивості невизначеного інтегралу Постійний множник можна винести за знак інтегралу: Інтеграл від алгебраїчної суми скінченого числа функції дорівнює алгебраїчній сумі інтегралів від цих функції: Похідна від невизначеного інтегралу дорівнює підінтегральній функції: Невизначений інтеграл від диференціалу неперервно диференційованої функції дорівнює, з точністю до сталого додатка, самій цій функції: Якщо дві функції тотожно рівні, то їх первісні можуть відрізнятися лише постійним додатком. план
4.Основні методи інтегрування Безпосереднє інтегрування – проводиться за допомогою таблиць без додаткових перетворень. Метод розкладання – базується на розкладанні підінтегральної функції на суму функцій, кожна з яких є табличною. Інтегрування підстановкою – полягає у заміні змінної в інтегралі. Інтегрування частинами – полягає в отриманні добутку двох неперервних функцій. план
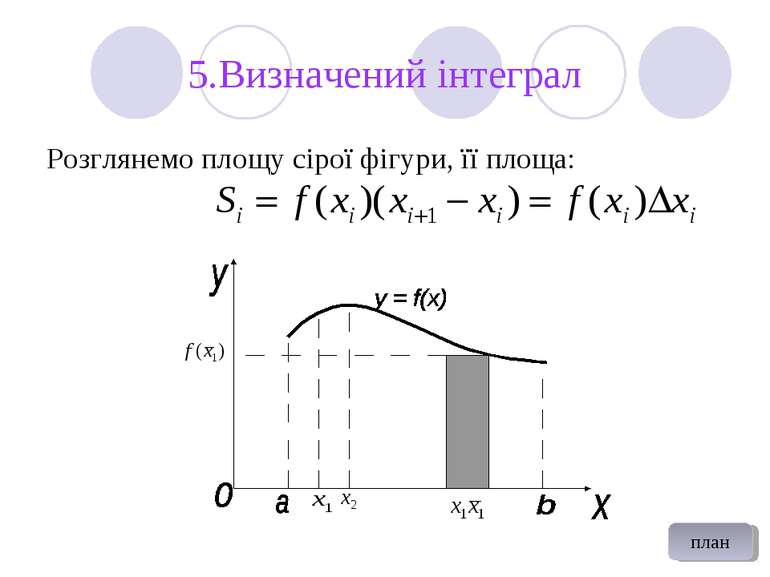
Визначений інтеграл Ця величина буде тим точніше давати площу криволінійної трапеції, чим менше . Точне значення площі дається границею: Величина називається інтегральною сумою, або сумою Дарбу. Визначення: якщо границя інтегральної суми існує при всіх , то ця границя називається визначеним інтегралом від функції на відрізку і починається символом:
6.Властивості визначеного інтеграла Постійний множник можна виносити за знак інтеграла: Інтеграл від алгебраїчної суми функцій дорівнює сумі визначених інтегралів від додатків: план
Якщо відрізок [a, b] = [c, b] + [c, b], то Теорема про середнє. Якщо функція f (x) неперервна на [a, b], то у межах [a, b] існує точка така, що
При перестановці меж інтегрування інтеграл змінює знак на протилежний Якщо межі інтегрування нескінченно мало відрізняються одна від одної, то
Похідна по х від інтеграла зі змінною верхньою межею ч дорівнює підінтегральній функції при значенні змінної, рівна значенню верхньої межі (t = x): інтеграл зі змінною верхньою межею є однією із первісних для підінтегральної функції.
7. Формула Ньютона-Лейбніца Знаючи, що , знайдемо С. Прийнявши х = а, матимемо . Звідси F (a) + C, Тобто C = -F (a). Отже, Перейдемо до означеного інтеграла, прийнявши. Остаточно будемо мати Ця формула називається формулою Ньютона-Лейбніца. Задача обчислення визначеного інтеграла зводиться до знаходження первісної, потім треба обчислити значення первісної при x = b i x = a та знайти різницю цих чисел. план
8. Практичне заняття Приклад. Обчислити визначений інтеграл. Розв'язок: використовуючи властивості 1 і 2 невизначеного інтеграла, даний інтеграл можна записати у вигляді: Використавши формулу 1 з таблиці невизначених інтегралів, отримаємо план
10. Питання по матеріалу Як звучить визначення теореми про існування похідної? Назвати основні властивості невизначеного інтегралу. Назвати основні методи інтегрування. Яка різниця між визначеним та невизначеним інтегралом? У чому полягає теорема Ньютона-Лейбніца? план
1.Поняття про диференціальні рівняння Диференціальним називається рівняння, в яке, крім функції у і незалежної змінної х, входять похідні функції (або диференціали dx i dy). Загальний вигляд диференціального рівняння у випадку функції однієї змінної: план
Найбільш поширені у фізиці диференціальні рівняння в частинних похідних: Рівняння дифузії: де шукана функція – концентрація речовини є функцією часу і координати c = f (x, t), D – коефіцієнт дифузії. Рівняння теплопровідності для температури Т = f (x, t): Χ – коефіцієнт температуропроводності.
Рівняння вільних гармонічних коливань: де ω – власна величина, s – зміщення тіла від положення рівноваги. Хвильове рівняння: де s = f (x, t) – зміщення точок середовища від положення рівноваги, v – швидкість поширення хвилі.
2. Лінійні диференціальні рівняння Лінійне диференціальне рівняння має вигляд: Теорема про існування єдиного частинного розв'язку диференціального рівняння Якщо функція і її частинна похідна неперервні у деякій області, то існує в даній області єдиний розв'язок у = φ (х) цього рівняння, для якого справедливо: якщо , то . план
3. Диференціальні рівняння зі змінними, що розділяються Даний метод розв'язання лінійних рівнянь базується на інтегруванні лівої та правої частин почергово. Після цього легко знайти незалежну змінну. Прикладом може бути рівняння, яку описує процес розчинення лікарського препарату в організмі: де m – маса препарату в момент часу t, k – константа елімінації. план
Розв'язок: враховуючи, що , отримаємо Проінтегрувавши ліву і праву частини, маємо: Позначивши сталу через С, отримаємо загальний розв'язок рівняння: Щоб визначити константу С, треба лише знати початкові умови.
4. Лінійні диференціальні рівняння другого порядку з постійними коефіцієнтами Звичайне диференціальне рівняння другого порядку має вигляд: Загальний вигляд неоднорідного диференціального рівняння другого порядку: де f (x) – доданок, вільний від невідомої функції план
5. Практичне заняття Приклад: розв'язати диференціальне рівняння Розв'язок: складаємо характеристичне рівняння Його корені: Отже розв'язок має вигляд: план
7. Запитання по матеріалу Яке рівняння називається диференціальним? Назвіть найбільш поширені диференціальні рівняння в частинних похідних. У чому полягає суть теореми про існування єдиного частинного розв'язку? Який основний метод розв'язку диференціальних рівнянь із змінними, що розділяються? Зобразіть вигляд звичайного диференціального рівняння другого порядку. план
Частота та ймовірність події Частота події – це відношення числа випробувань , в яких дана подія реалізується, до повного числа випробувань : Частота події при великому числі випробувань втрачає випадковий характер Ймовірність Р(А) випадкової події А називається границя , до якої наближається частота події А при необмеженому зростанні повного числа випробовувань , тобто Ймовірність будь-якої події задовольняє подвійну нерівність 0≤P(A)≤1
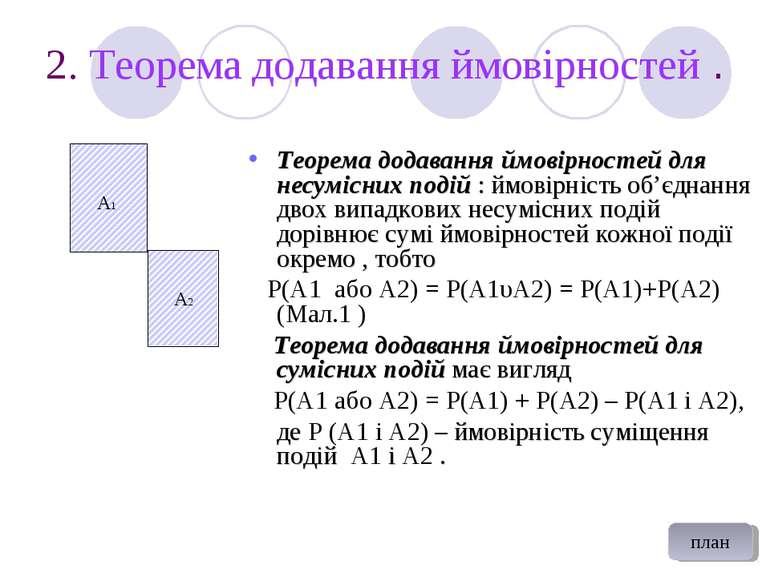
2. Теорема додавання ймовірностей . A1 A2 Теорема додавання ймовірностей для несумісних подій : ймовірність об’єднання двох випадкових несумісних подій дорівнює сумі ймовірностей кожної події окремо , тобто P(A1 або A2) = P(A1υA2) = P(A1)+P(A2) (Мал.1 ) Теорема додавання ймовірностей для сумісних подій має вигляд P(A1 або A2) = P(A1) + P(A2) – P(A1 і A2), де Р (А1 і А2) – ймовірність суміщення подій А1 і А2 . план
3.Теорема множення ймовірностей. Теорема множення ймовірностей для незалежних подій : ймовірність суміщення (перетину) двох незалежних подій дорівнює добутку ймовірностей цих подій , тобто P(A1 і A2) = P(A1 חA2) = P (A1) P (A2). Теорема множення ймовірностей для залежних подій: ймовірність суміщення (перетину) двох залежних подій дорівнює добутку умовної ймовірності РА(В) на ймовірність реалізації події А-Р(А) P(A і B) = P(A)PА(В) у випадку незалежних подій А і В РА (В) = P(B) план
4.Формула повної ймовірності . Формули Байєса . Якщо подія А може реалізуватись тільки при виконанні однієї з подій В1 , В2 , …, Вп , які утворюють повну групу несумісних подій , то ймовірність події А обчислюється за формулою : P(A) =P(B1)PB1(A) + P(B2)PB2(A) +…+P (Bn) Pn (A) – формула повної ймовірності . Формули Байєса : PA (Bi)= план
5.Повторні випробування . Формула Бернуллі . Припустимо , що проводиться декілька випробувань , причому ймовірність події А у кожному випробуванні не залежить від результатів інших випробувань . Знайдемо ймовірність того , що подія А реалізується рівно m разів у серії з n випробувань . Ця ймовірність визначається формулою : де р – ймовірність появи події А в одному досліді ; – ймовірність того , що подія А не з’явиться в одному досліді ; - число можливих комбінацій із n елементів по m . план
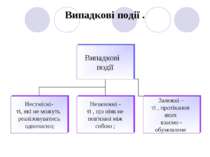
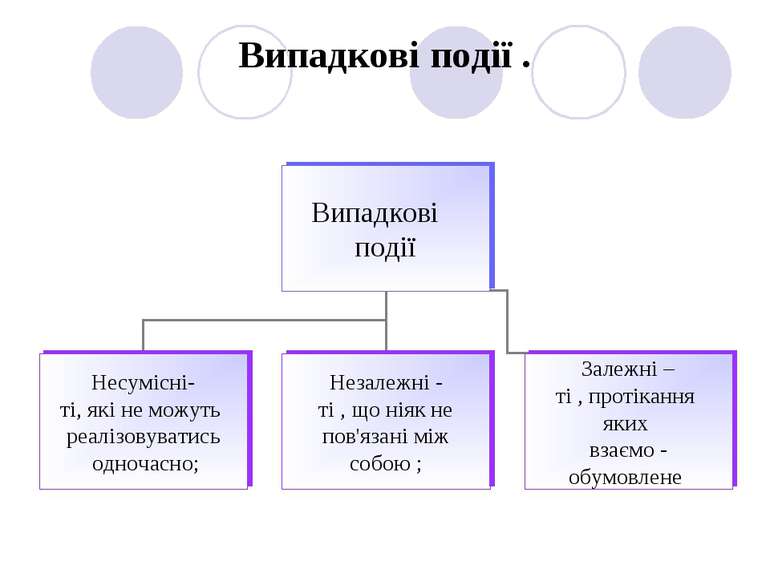
6.Випадкова величина , дискретні та неперервні випадкові величини . Випадковими називаються величини , які у результаті випробувань можуть набувати різних числових значень за однакових умов випробувань. Випадкові величини бувають : 1. Дискретними , тобто такими , які набувають скінченну множину значень і їх можна пронумерувати. 2. Неперервними , тобто такими , які набувають будь-які значення всередині заданого інтервалу. план Х1 Х1 Х2 … Хn-1 Xn P1 P1 P2 … Рn-1 Pn
Розподілом дискретної випадкової величини Х називається множина її можливих значень Х1 , Х2 ,Х3 , …, Хn і ймовірностей Р1 , Р2 , Р3 , …, Рn , які відповідають цим значенням випадкової величини . Як правило , розподіл випадкової дискретної величини характеризується таблицею Х1 Х1 Х2 … Хn-1 Xn P1 P1 P2 … Рn-1 Pn
7(а). Інтегральна функція розподілу. Інтегральна функція розподілу(інтегральним законом розподілу) випадкової величини Х називається функція F (x) , яка дорівнює ймовірності того , що випадкова величина Х прийме значення менше , ніж х : F (x) = P(Xх2, то F (х1) ≤F (х2) 3. P (a ≤X< b) = F (b) –F (a) 4. F (X=x0) = 0 5. P (a< X
7(б). Диференціальна функція розподілу Диференціальною функцією розподілу називається функція f (x) , яка дорівнює похідній інтегральної функції розподілу Ймовірність того , що неперервна випадкова величина Х набуватиме значення з деякого інтервалу (a ; b) , дорівнює визначеному інтервалу від її щільності розподілу f (x) з межами інтегрування a і b: (а
8.Основні кількісні характеристики розподілу випадкових величин . 1. Математичне сподівання або середнє значення випадкової величини 2. Дисперсія D (X) випадкової величини Х : Інший вираз для дисперсії має вигляд : D (X) = M (X ) – M (X) Таким чином , дисперсія – це різниця математичного сподівання квадрата випадкової величини і квадрата математичного сподівання цієї величини. 3. Середнє квадратичне відхилення ơ (Х) пов’язане з дисперсією формулою : Видно , що розмірність ơ збігається з розмірністю самої випадкової величини Х . план
9.Основні закони розподілу випадкових величин Основні закони розподілу випадкових величин : 1. Біноміальний розподіл . 2. Розподіл Пуассона . 3. Нормальний розподіл ( розподіл Гаусса) . 4. Функція Лапласа . Біноміальний розподіл Біноміальний розподіл – це розподіл імовірностей , які визначається формулою Бернуллі Подаємо біноміальний розподіл у вигляді таблиці план X 0 1 … m … n P … …
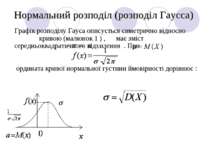
Нормальний розподіл (розподіл Гаусса) Графік розподілу Гауса описується симетрично відносно кривою (малюнок 1 ) , має зміст середньоквадратичного відхилення . При ордината кривої нормальної густини ймовірності дорівнює :
При зменшенні ця ордината необмежено зростає . При цьому крива пропорційно витягується вздовж осі ординат , так що її площа залишається рівною одиниці (малюнок 2 ) . Нормальний розподіл з параметрами та називають нормованим . Щільність розподілу в такому випадку дорівнює :
Функція Лапласа . Функція називається функцією Лапласа , за її допомогою можна знайти ймовірність потрапляння значень нормально розподіленої випадкової величини у будь-який відрізок числової осі . Для функції Лапласа складені таблиці , схожі з широко відомими таблицями логарифмів чи тригонометричних функцій.
10.Кореляційна залежність . Для характеристики кореляційного ефекту між випадковими величинами використовують коефіцієнт r кореляції , який є мірою залежності між цими величинами. Визначається формулою: Якщо випадкові величини не залежать одна від одної , то r = 0 . Коефіцієнт кореляції може набувати максимальне значення , рівне +1 та -1 . Тісна кореляція ( 0.7< r r >0.4 ) ; практична відсутність кореляції ( r < 0.4 ) . план
11. Практичне заняття Приклад: за статистичними даними, групу крові А мають 36,9% осб всіх європейців, групу В – 23,5%, групу АВ – 0,6%, групу О – 39%. Знайти ймовірність того, що у довільно взятого донора-європейця група крові А або В. Розв'язок: згідно із статистичним визначенням імовірностей, P (A) = 0,369, P (B) = 0,235. використовуючи теорему додавання ймовірностей для несумісних подій, одержимо
12.Завдання для самостійної роботи В ящику знаходиться 10 кульок: 3 білих та 7 чорних. З нього навздогад витягають одну кульку. Яка ймовірність того, що ця кулька буде білою? Чорною? Знайти ймовірність сумісної появи герба при одному киданні двох монет. Яка ймовірність того, що в сім'ї чотирма дітьми будуть діти різної статі?
13.запитання по матеріалу Розтлумачте поняття про частоту події . Поясніть теорему додавання ймовірностей. Для чого використовуються формули Байєса? Розповісти про величини та класифікацію явищ. у чому суть функції Лапласа?
Томас Байєс Томас Байєс ( 1702 – 1761рр.) англійський математик , член Лондонського об’єднання . Народився в Лондоні . Отримав домашню освіту . Математичні дослідження Байєса відносяться до теорії ймовірностей (теорія Байєса). Перша робота була опублікована у 1763р. Друга його робота “Нотатки по вирішенню проблеми доктрини шансів” була опублікована у 1958р. Збереглась термінологія : байєвський підхід до статичних законів, байєвська оцінка рішення та інші . план
Д. Пуассон . Пуассон Сімеон Дені ( 1781 – 1840 рр.) – французький математик, фізик, механік. Член Паризької академії наук (1812 р.). Народився в Пітів’є. В 1798 р. Поступив в політехнічну школу. По закінченню курсу був залишений при цьому навчальному закладі. З 1816 р. –професор в Сорбоні. Пуассон розробив багато розділів математичної фізики, дав вирішення багатьох задач електростатики. В 1829 р. Пуассон започаткував теорію девіації. В його дослідженнях прикладного характера важливе місце займають роботи по зовнішній балістиці та гідродинаміці. Важливе значення мають роботи Пуассона, посвячені інтегралам, теорії ймовірності, рядам. Покращив способи використання теорії ймовірності взагалі і до питань статистики, а також довів теорему, яка відносилась до закону великих чисел, вперше використавши термін “закон великих чисел”. В загальній теорії рівнянь Пуассону належить оригінальний метод виключення перемінних. В диференціальній геометрії йому належить робота про кривизну поверхностей . план
Карл Фрідріх Йоганн Фрідріх Карл Гаусс ( 1777 – 1855 рр. ) народився 30 квітня 1777 р. В три роки він вже вмів рахувати і виконувати елементарні обчислення. Одного разу в обчисленнях свого батька його трьохрічний син помітив помилку. У 1784 р. Карл пішов в школу. Карл залишив батьківський дім у 1788 р. , коли поступив до школи наступного ступеню. В новій школі він добре вивчив латинську мову. В 1791 р. Гаусс, в якості талановитого молодого громадянина, був представлений царю. У 1792-1795 рр. навчався в Колегії Карла . В 1795 р. Поступив у Геттингенський університет. Восени 1798 р. залишив університет і 16 червня наступного року Гаусс отримав ступінь доктора філософії. 9 жовтня 1805р. Гаусс одружився на Йоганні Остгроф. У 1809 р. Йоганна померла і через деякий час Карл заручився з Фредерикою Вальдек. Але другий шлюб не був щасливим і після довгої хвороби дружина померла в 1831 р. Сини Карла емігрували в Америку і Філадельфію. Гаусс помер 23 лютого 1855 р. план
П’єр – Сімон Лаплас П’єр – Сімон Лаплас ( 1749 – 1827 рр. ) – французький математик, фізик, член багатьох академій і інститутів. Народився в Нормандії. Вчився в школі ордену ченців - бенедиктів. Досконало вивчив давні мови, літературу і мистецтво, вивчав математику і астрономію. В сфері математики Лаплас створив роботи по теорії диференціальних рівнянь. Ще при житті вченого тричі видавалась його “ Аналітична теорія вірогідностей” (1812 р.) . Лаплас розвинув методи небесної механіки і завершив пояснення руху тіл Сонячної системи на основі закону всесвітнього тяжіння Ньютона. В 1780 р. Лаплас запропонував новий спосіб обчислення орбіт небесних тіл. Довів, що кільце Сатурна не може бути суцільним. Лаплас розробив теорію руху супутників Юпітера (1789 р.) , відкрив причини прискорення Місяця (1787 р.), виявив причину стиснення Землі біля полюсів. Результати дослід-жень в області небесної механіки виведені в класичному трактаті “Трактаті про небесну механіку” (1798 – 1825 рр. ) план
Схожі презентації
Категорії














































![Якщо відрізок [a, b] = [c, b] + [c, b], то Теорема про середнє. Якщо функція ... Якщо відрізок [a, b] = [c, b] + [c, b], то Теорема про середнє. Якщо функція ...](https://svitppt.com.ua/images/10/9741/770/img48.jpg)

















































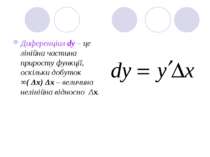
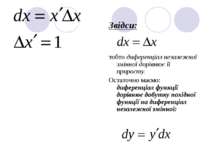
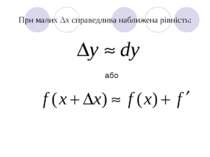



































![Якщо відрізок [a, b] = [c, b] + [c, b], то Теорема про середнє. Якщо функція ... Якщо відрізок [a, b] = [c, b] + [c, b], то Теорема про середнє. Якщо функція ...](https://svitppt.com.ua/images/10/9741/210/img48.jpg)