Презентація на тему:
“Функція”

“Функція” 10 клас (академічний рівень) Підготувала: Кряжева Олена Петрівна вчитель математики Боровиківського НВК Звенигородської районної ради Черкаської області

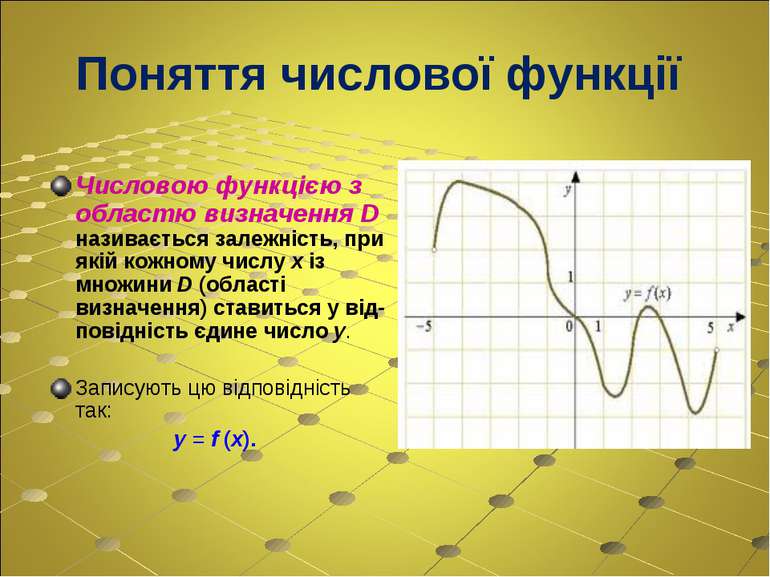
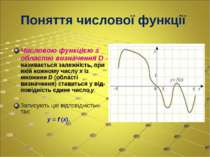
Поняття числової функції Числовою функцією з областю визначення D називається залежність, при якій кожному числу x із множини D (області визначення) ставиться у від- повідність єдине число y. Записують цю відповідність так: y = f (x).

Позначення і терміни D (f) — область визначення E (f) — область значень x — аргумент (незалежна змінна) y — функція (залежна змінна) f — функція f (x0) — значення функції f у точці x0

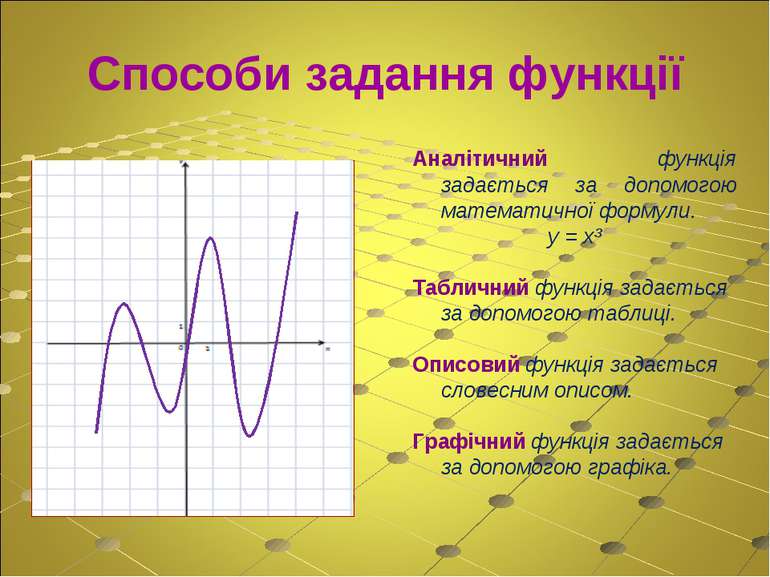
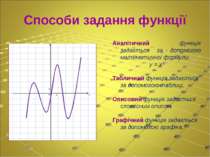
Способи задання функції Аналітичний функція задається за допомогою математичної формули. у = х³ Табличний функція задається за допомогою таблиці. Описовий функція задається словесним описом. Графічний функція задається за допомогою графіка.

Приклад 1 Знайдіть область визначення функції: 1) y = x² + x; 2) у = 3) у =

Приклад 2 Знайдіть область значень функції: 1) y = x² – 3. 2) у = –3х + 1; 3) у =

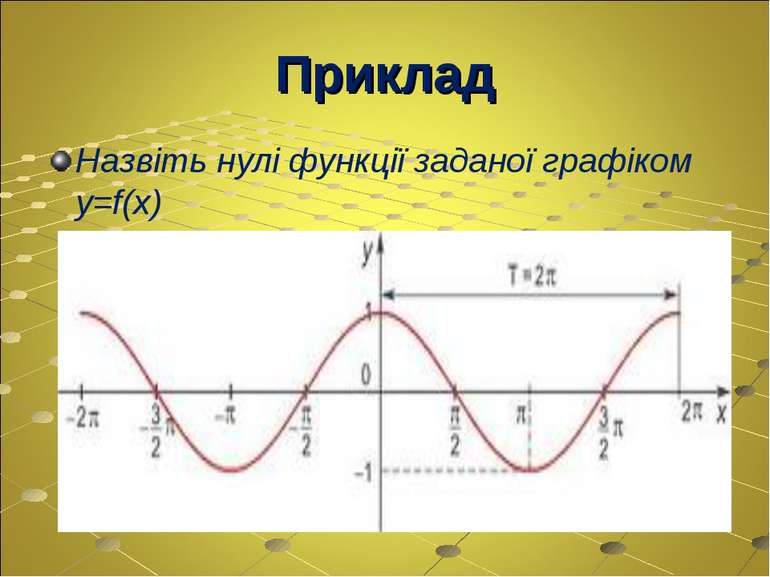
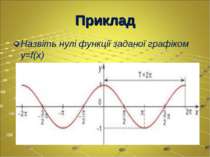
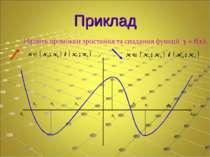
Нулі функції Якщо для функції y=f(x) виконується умова f(x0)=0 (х0 є D(f)), то х0 – нуль функції. х1, х2, х3 – нулі функції (f(x1)=f(x2)=f(x3)=0) проміжки знакосталості функції - - + +

Приклад Назвіть нулі функції заданої графіком y=f(x)

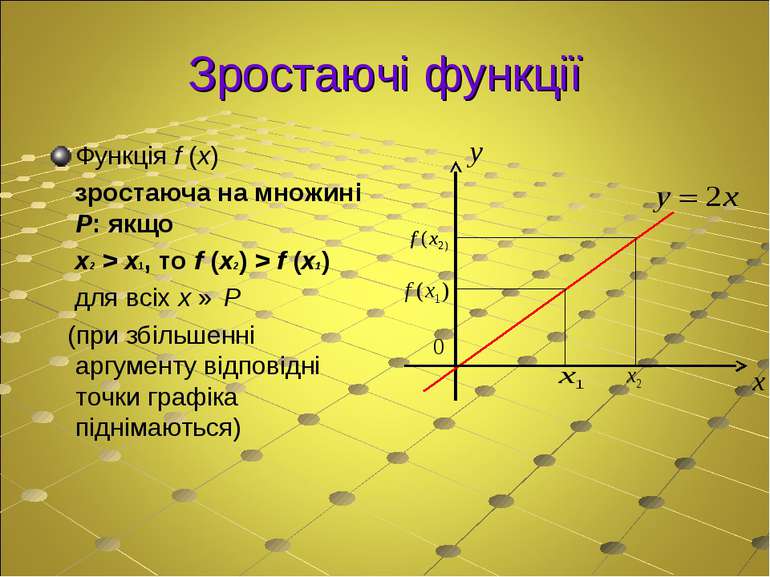
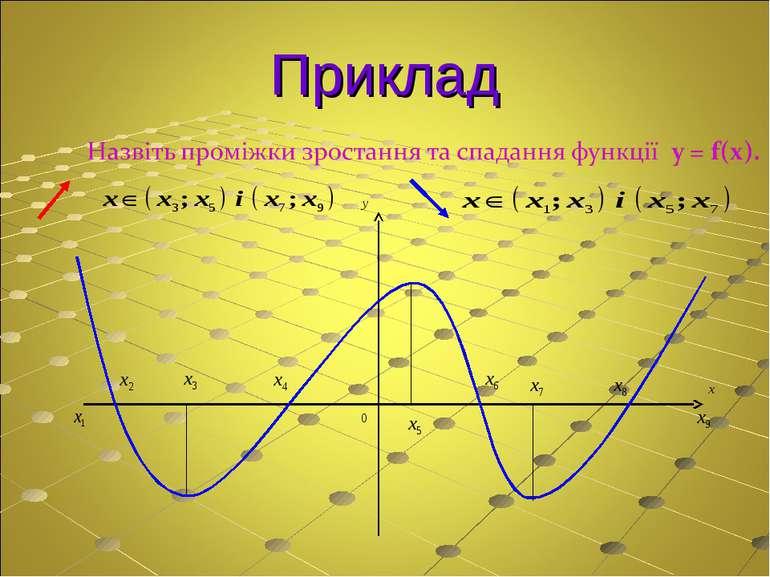
Зростаючі функції Функція f (x) зростаюча на множині P: якщо x2 > x1, то f (x2) > f (x1) для всіх x ∈ P (при збільшенні аргументу відповідні точки графіка піднімаються)

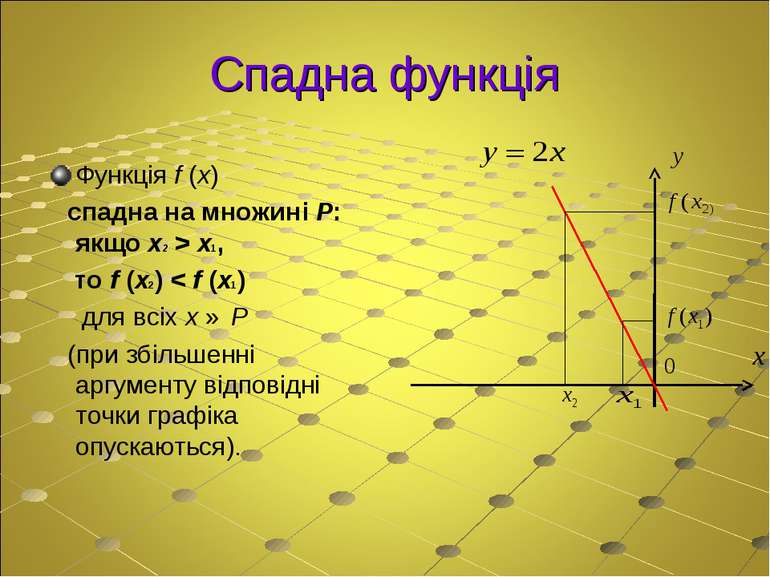
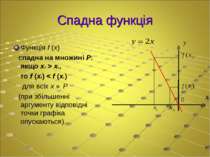
Спадна функція Функція f (x) спадна на множині P: якщо x2 > x1, то f (x2) < f (x1) для всіх x ∈ P (при збільшенні аргументу відповідні точки графіка опускаються).

Приклад

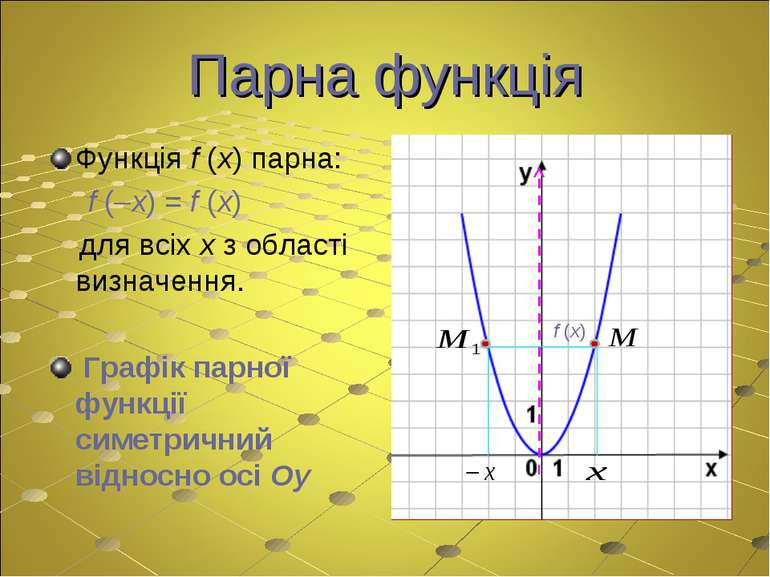
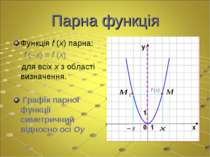
Парна функція Функція f (x) парна: f (–x) = f (x) для всіх x з області визначення. Графік парної функції симетричний відносно осі Oy f (x)

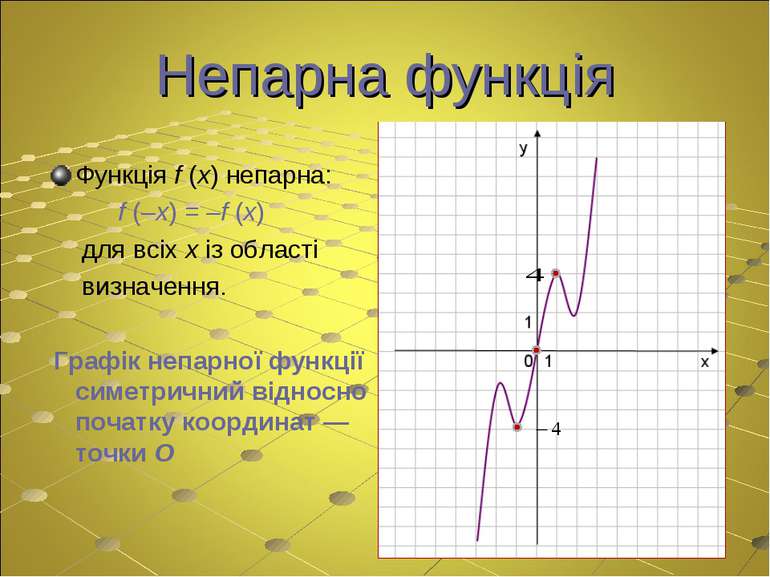
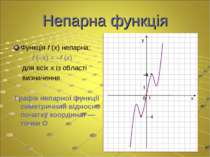
Непарна функція Функція f (x) непарна: f (–x) = –f (x) для всіх x із області визначення. Графік непарної функції симетричний відносно початку координат — точки О

Приклад Доведіть, що при k ≠ 0 областю значень лінійної функції y = kx + b є множина всіх дійсних чисел. РОЗВ’ЯЗАННЯ: Якщо kx + b = a (де k ≠ 0), то розв’язок цього рівняння x . а, b ,k − існує для будь-якого a ∈ R (k ≠ 0 за умовою). Таким чином, значенням заданої функції може бути будь-яке дійсне число, отже, її область значень E (f) = R. КОМЕНТАР Позначимо значення заданої функції f (x) (тобто kx + b) через a і з’ясуємо, для яких a можна знайти відповідне значення x, таке, що f (x) = a. Множина всіх таких значень a і буде складати область значень функції f (x).

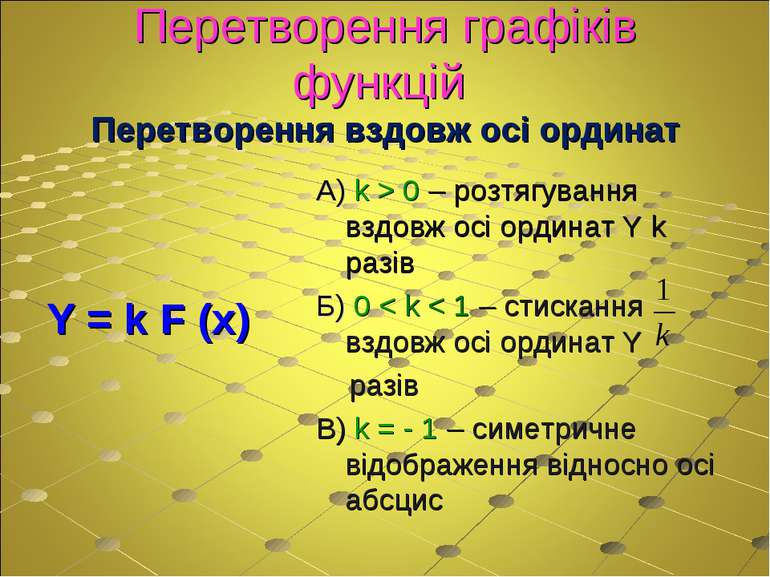
Перетворення графіків функцій Перетворення вздовж осі ординат Y = k F (x) А) k > 0 – розтягування вздовж осі ординат Y k разів Б) 0 < k < 1 – стискання вздовж осі ординат Y разів В) k = - 1 – симетричне відображення відносно осі абсцис

Перетворення вздовж осі ординат Y = F (x) + b Паралельне перенесення осі ординат на І b І одиниць: А) вгору, якщо b > 0; Б) вниз, якщо b < 0

Перетворення вздовж осі ординат Y = І F (x) І Збереження частин графіка, які лежать над віссю Ох і симетричне відображення відносно осі Ох тих частин графіка, які розташовані нижче від осі Ох.

Перетворення вздовж осі абсцис Y = F (x + a) Паралельне перенесення вздовж осі абсцис на І а І одиниць: А) ліворуч, якщо а > 0; Б) праворуч, якщо а < 0

Перетворення вздовж осі абсцис Y = F ( n x ) А) n > 0 – стискання вздовж осі абсцис у n разів Б) 0 < n < 1 –розтягування вздовж осі абсцис у разів В) n = - 1 – симетричне відображення відносно осі ординат

Перетворення вздовж осі абсцис Y = F І x І Відкидання частин графіка, які лежать ліворуч від осі Оу і збереження та відображення симетрично осі Оу тих частин графіка, які розташовані у правій напівплощині

Математичний термін функція вперше з’явився в 1692р у Лейбніца, як зв’язок різних відрізків з довільною кривою

Початкове поняття функції, як функціональну залежність та її графічне зображення ввів Ферма .

Перше загальне визначення функції зустрічається у Іоанна Бернуллі (1718р).

Сучасне визначення числової функції, як довільної відповідності чисел вводе Ейлер (1755р)

Література 1. Мерзляк А.Г.,Номіровський Д.А.,Полонський В.Б., Якір М.С. Алгебра і початки аналізу. (Академічний рівень) 10 клас .- Х.: Гімназія, 2010. 2.Нелін Є.П. Алгебра і початки аналізу.(Академічний рівень) 10 клас. - Х.: Гімназія, 2010. 3. Бевз Г.П. Алгебра. (Академічний рівень)10 клас. – Х.: Гімназія, 2010

Інтернет ресурси http://formula.co.ua http://college.ru http://wikipedia.org