Презентація на тему:
Історія розвитку інтегралів

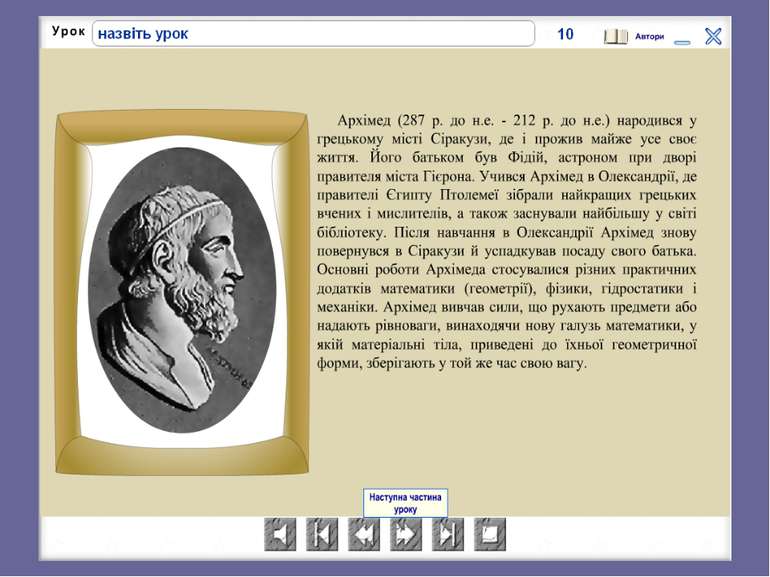
Історія розвитку понять інтеграла й інтегрального обчислення Історія розвитку понять інтеграла й інтегрального обчислення пов’язана з потребою в обчисленні площ фігур, а також поверхонь і об’ємів довільних тіл. Передісторія інтегрального обчислення сягає глибокої давнини: ідеї інтегрального обчислення можна знайти в роботах давньогрецьких учених Евдокса Кнідського (бл.408-355 до н.е.) і Архімеда (бл.287-212 до н.е.).

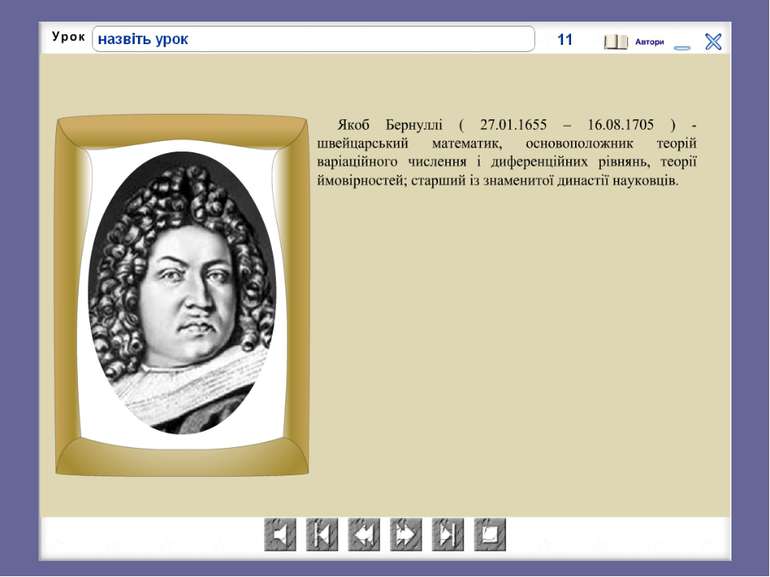
Математики XVII ст.. училися на працях Архімеда. Німецький астроном Й.Кеплер застосував подібні методи. Італійський математик Б.Кавальєрі, уявивши кожну фігуру утвореною з відрізка, а тіло із плоских фігур, сформулював принципи, які вважав очевидними й приймав без доведення. Символ ∫ - змінену латинську букву S (summa) – запровадив Г.Лейбніц, слово «інтеграл» - швейцарець Я.Бернуллі. Більш раннє поняття «примітивна функція», уведене Ж.Лагранжем, пізніше було замінено на поняття «первісна для функції», що його застосовують і зараз. Позначення визначеного інтеграла увів К.Фурьє.

Й.Кеплер К.Фур’є Ж.Лагранж

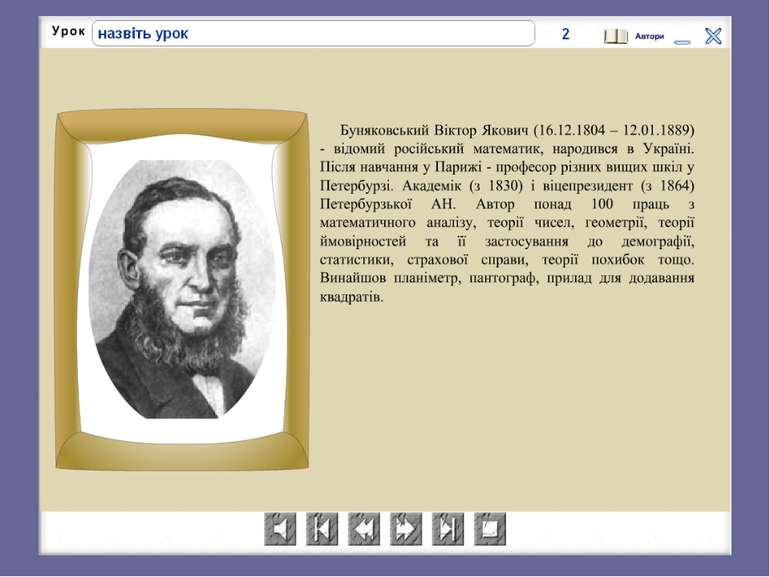
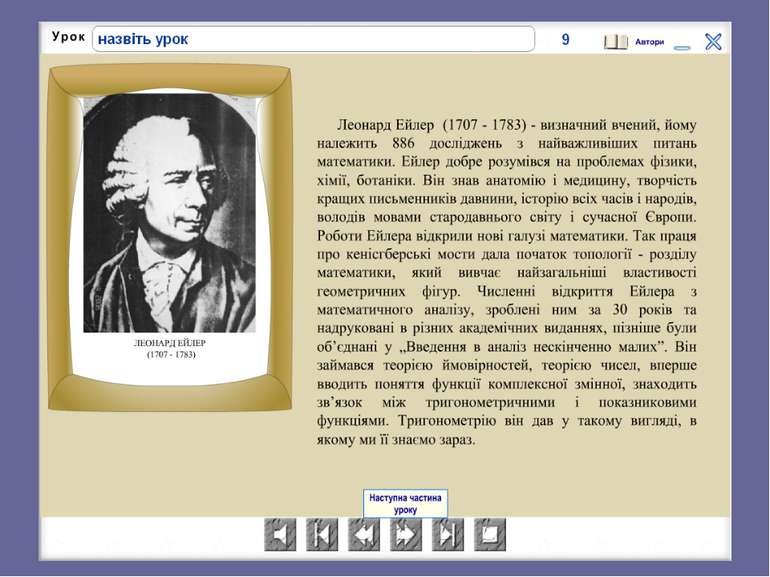
Слід зазначити, що в XVII ст.. інтегрального обчислення як такого ще практично не було. Зв’язок між операціями диференціювання й інтегрування, узагальнення ідей, на яких ґрунтується розв’язання багатьох задач, було знайдено І.Ньютоном і Г.Лейбніцем: незалежно один від одного учені відкрили вираз, відомий зараз як формула Ньютона – Лейбніца. У XIX ст. методи інтегрального обчислення активно розвивав Л.Ейлер, також значний внесок зробили російські математики М.В.Остроградський, В.Я.Буняковський та П.Л.Чебишев.

У XX ст. теорія інтегралів була суворо викладена в роботах О.Коші, Б.Рімана, Г.Дарбу. Відповіді на низку питань, пов’язаних з обчисленням площ і об’ємів фігур, були отримані разом зі створенням К.Жорданом (1838-1922) теорії міри.