Презентація на тему:
Теорема Піфагора. Розв’язування задач прикладного та практичного направлення.

Теорема Піфагора. Розв’язування задач прикладного та практичного направлення.

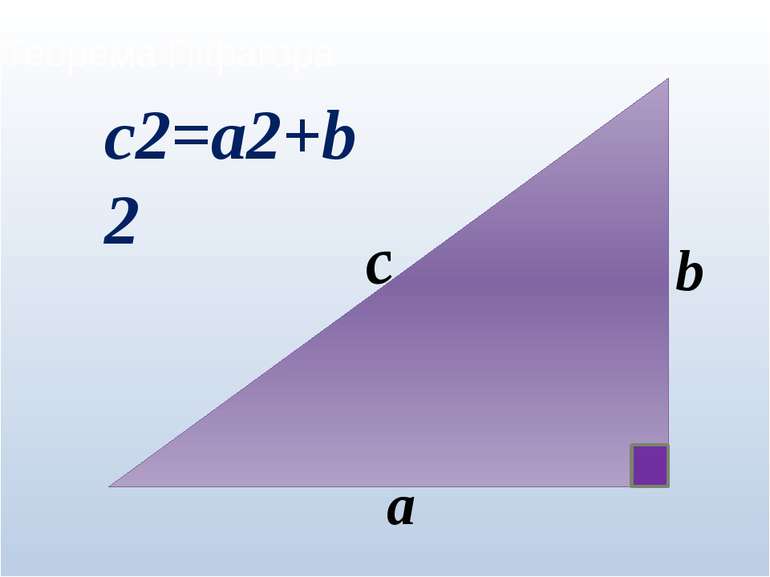
П Р Я М О К У Т Н И Й Г О С Т Р І П І Ф А Г О Р І Й С Ь К А К А Т Е Т И Г А Р М О Н І Я Г І П О Т Е Н У З А С Т О Р О Н И Ч О Т И Р И 1 2 3 4 5 6 7 8 П І Ф А А Г О Р Кросворд Як називається трикутник, для якого можна застосувати теорему Піфагора? Які ще кути, крім прямого, може мати прямокутний трикутник? Як називалась школа, яку заснував Піфагор? Як називаються сторони прямокутного трикутника, що утворюють прямий кут? Як називається найбільша сторона прямокутного трикутника? Скільки наук вивчалося в Піфагорійській школі? Що можна знайти в прямокутному трикутнику за допомогою теореми Піфагора? Піфагор вважав, що в основі всього лежать числа і ….. Теорема Піфагора c2=a2+b2 b c а

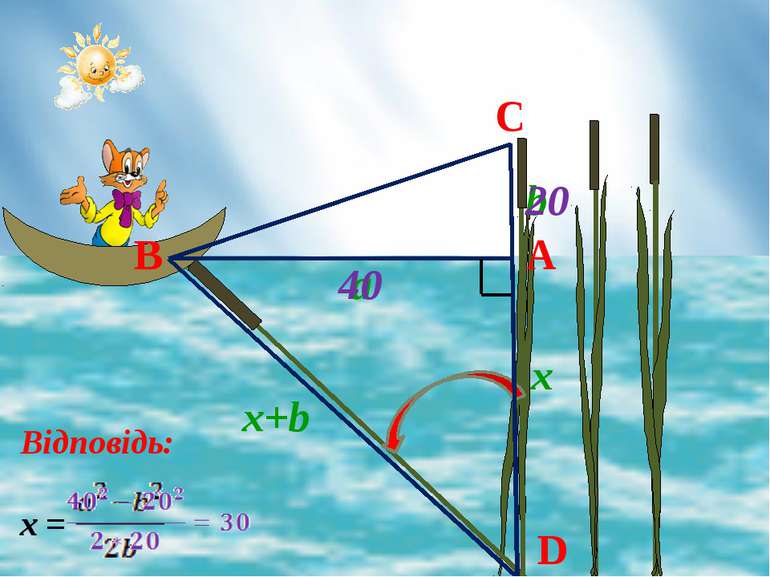
Мета: забезпечити під час уроку закріплення основних понять по темі "Теорема Піфагора"; продовжити формування вміння будувати математичні моделі при розв’язуванні задач практичного змісту; розвивати пізнавальний інтерес учнів.

«Зближення теорії з практикою дає найбільш вигідні результати, і не одна тільки практика від цього виграє ". П.Л. Чебишев

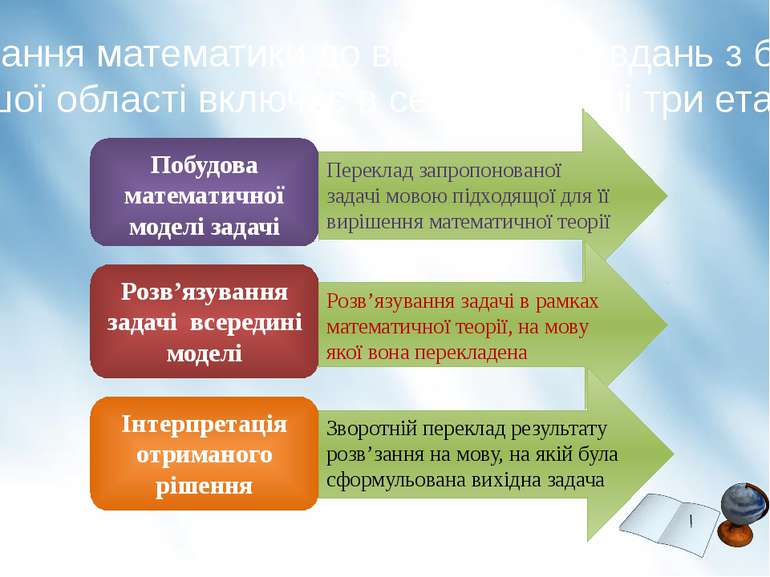
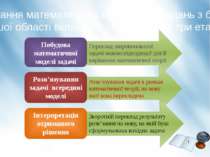
Побудова математичної моделі задачі Розв’язування задачі всередині моделі Інтерпретація отриманого рішення Переклад запропонованої задачі мовою підходящої для її вирішення математичної теорії Розв’язування задачі в рамках математичної теорії, на мову якої вона перекладена Зворотній переклад результату розв’зання на мову, на якій була сформульована вихідна задача Застосування математики до вирішення завдань з будь-якої іншої області включає в себе наступні три етапи

B А C D b a x x+b Відповідь: x = 40 20

«Причина популярності теореми Піфагора триєдина – це краса, простота і значущість".

Підсумок уроку За що ти можеш себе сьогодні ПОХВАЛИТИ? Що тобі ВДАЛОСЯ сьогодні на уроці? Над чим ще потрібно ПОПРАЦЮВАТИ? Навіщо нам був потрібний цей урок?

Дякую за урок!