Презентація на тему:
Перпендикулярність прямої та площини

Перпендикулярність прямої і площини Викладач вищої категорії, старший викладач Ларіонова О.М. Міністерство освіти і науки України Департамент освіти, науки та молоді Миколаївської облдержадміністрації Навчально-методичний центр професійно-технічної освіти в Миколаївській області Вознесенський професійний аграрний ліцей

І. Організаційний момент уроку: привітання, перевірка готовності до уроку (робочих зошитів, підручників, письмового приладдя). Мета уроку: Сформувати в учнів поняття про пряму, перпендикулярну до площини, ознайомити з ознакою перпендикулярності прямої і площини, сформувати вміння застосовувати означення прямої, перпендикулярної до площини, ознаку перпендикулярності прямої і площини при розв'язуванні задач. Розвивати просторову уяву та логічне мислення учнів. Виховувати розуміння ролі математики в житті, розуміння важливості математичних знань. Тип уроку: урок засвоєння нових знань Обладнання: персональний комп'ютер; мультимедійний проектор; екран; авторська презентація, підготовлена за допомогою Microsoft Power

2. Подивіться на мал.2 Чи буде пряма а перпендикулярною до прямої с? Відповідь обґрунтуйте. а а с с В С Мал.1 Мал.2 в в Задача на розпізнавання 1. Подивіться на мал.1 Чи будуть прямі а і с перпендикулярні? Відповідь обґрунтуйте. ІІ. Перевірка домашнього завдання Запитання до класу 1. Дано пряму в просторі, на ній узято точку. Скільки можна побудувати прямих, що проходять через цю точку і є перпендикулярними до даної прямої? А на площині? 2. Дано пряму в просторі й точку поза нею. Скільки можна побудувати прямих, що проходять через цю точку і є перпендикулярними до даної прямої? А на площині?

m n k Завдання на конструювання поняття m і n – перпендикулярні Яке має бути взаємне розташування прямих n і k, щоб m і k були перпендикулярні? 2. Яке має бути взаємне розташування прямих m і k, щоб n і k були перпендикулярні?

Змоделюйте в кабінеті таку ситуацію: три променя ОМ, ОК, ОТ попарно перпендикулярні. Як розміщений кожен промінь по відношенню до площини, яка визначена двома другими променями? Завдання на моделювання О М К Т

ІІІ. Актуалізація опорних знань Запитання до класу Яким може бути взаємне розміщення прямої і площини? Які прямі називаються перпендикулярними? Чи завжди перпендикулярні прямі лежать в одній площині? В планіметрії ми вивчали перпендикулярність прямих. А які об'єкти, крім прямих, можуть бути перпендикулярні в просторі? IV. Формулювання теми, мети й завдань уроку. Первинна мотивація Сьогодні ми маємо дати відповідь на три запитання : «що вчити» , «як вчити», і «для чого вчити» і перевірити просту істину визначену ще Конфуцієм : «Три шляхи ведуть до знань : шлях міркувань – він найблагородніший, шлях наслідування - він найлегший і шлях досвід - він найгіркіший». Кожен із вас повинен поставити перед собою мету, над досягненням якої буде працювати на уроці. Подумайте, яка це може бути мета.

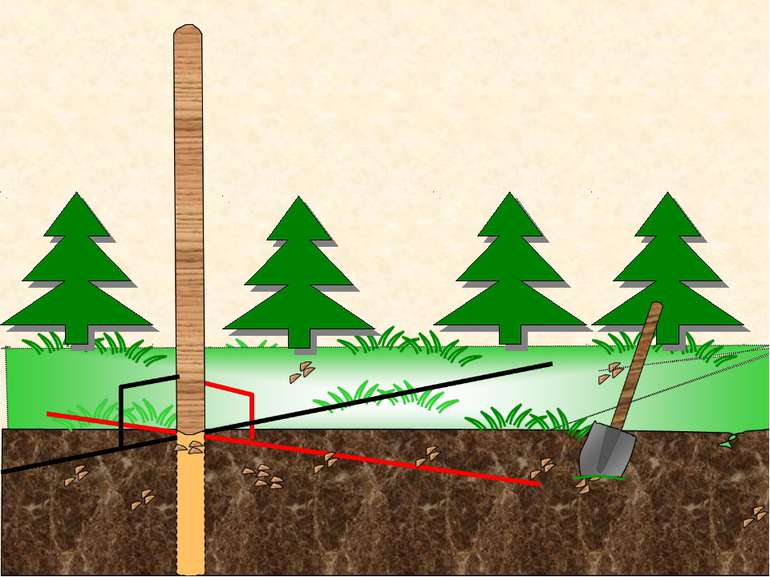
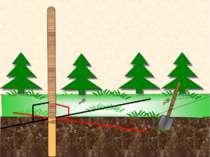
Необхідність перевіряти перпендикулярність прямої і площини на практиці виникає доволі часто. В яких об’єктах реального життя можна зустріти перпендикулярність прямої та площини?(учні дають відповіді). В житті ви, безперечно, мали змогу спостерігати, як кріпляться телевізійні вишки і антени, щогли вітрильників. Це наочні приклади перпендикулярів до площини ґрунту, палуби тощо.

Стереометричному матеріалу присвячено останні три книги «Початків» Евкліда, які написані близько 300 р. до н.е. XI книга містить теорію перпендикулярності прямої і площини. Цей матеріал в більшій своїй частині входить в даний час до підручника по стереометрії. Евклід дає таке означення: «Пряма перпендикулярна до площини, якщо вона перпендикулярна до всіх прямих, проведених в площині в точці, в якій вона цю площину зустрічає». V. Формування знань. Закріплення і підсилення мотивації.

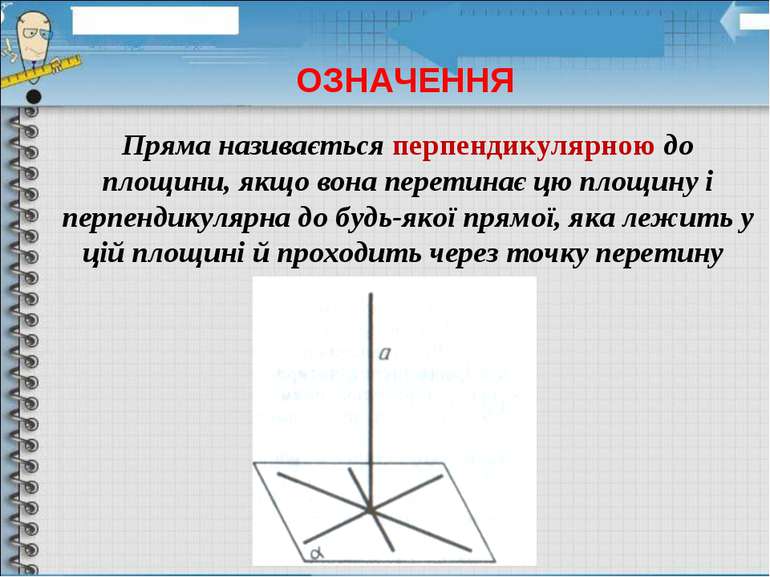
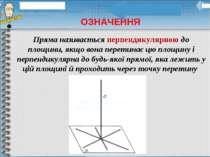
Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, яка лежить у цій площині й проходить через точку перетину ОЗНАЧЕННЯ

Постановка проблеми Потрібно зазначити, що перевірити в кожному випадку перпендикулярність прямої до всіх прямих площини неможливо. Життєва ситуація: як поставити стовп перпендикулярно поверхні Землі. Ваші дії. Відповідь: Дивлюся на стовп з двох сторін. Доб'юся того, щоб з обох сторін були прямі кути. Запитання до класу: 1. Як перевірити перпендикулярність прямої до даної площини? 2. Скільки прямих достатньо взяти, щоб відповісти на задане запитання?

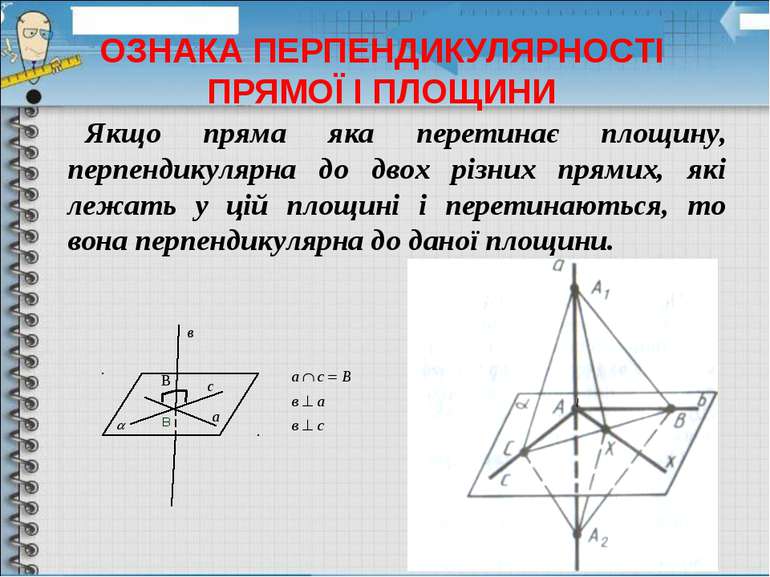
Якщо пряма яка перетинає площину, перпендикулярна до двох різних прямих, які лежать у цій площині і перетинаються, то вона перпендикулярна до даної площини. ОЗНАКА ПЕРПЕНДИКУЛЯРНОСТІ ПРЯМОЇ І ПЛОЩИНИ В с а в В

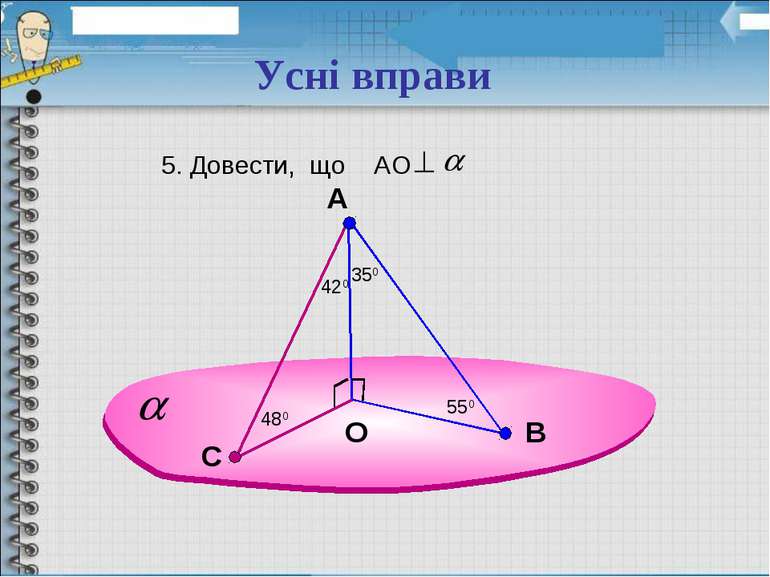
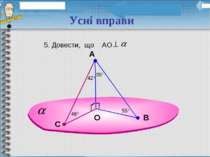
VІ. Формування вмінь і відпрацьовування навичок Усні вправи 1.Чи можна стверджувати, що пряма, яка проходить через центр круга і перпендикулярна до його діаметра, буде перпендикулярна до площини круга? 2. Чи можна стверджувати, що пряма, яка проходить через центр круга перпендикулярно двом радіусам, буде перпендикулярна до площини круга? 3. Чи можна стверджувати, що пряма, яка проходить через центр круга перпендикулярно двом діаметрам, перпендикулярна площині круга?

4. Дано: ABCD – куб Заповніть пропуски про взаємне положення прямих та площин: СС1…(DCB); AA1…(DCB); D1C1…(DCB); B1C1…(DD1C1); B1C1…DC1; A1D1…DC1; BB1…AC; A1B…BC; A1B…DC1 А D C B А1 D1 C1 B1 Формування вмінь і відпрацьовування навичок Усні вправи

O 350 420 С A В 550 480 5. Довести, що АО Усні вправи

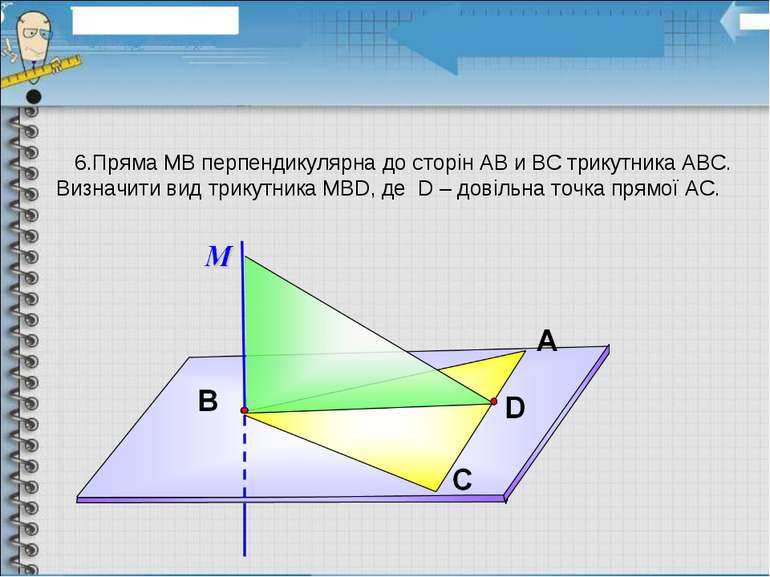
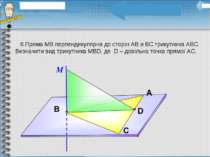
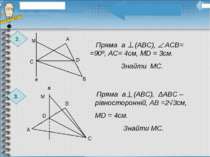
6.Пряма МВ перпендикулярна до сторін АВ и ВС трикутника АВС. Визначити вид трикутника МВD, де D – довільна точка прямої АС.

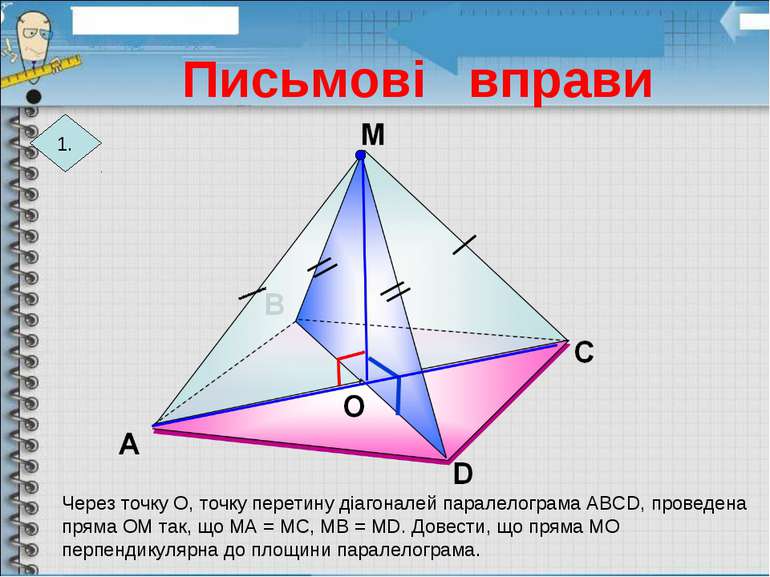
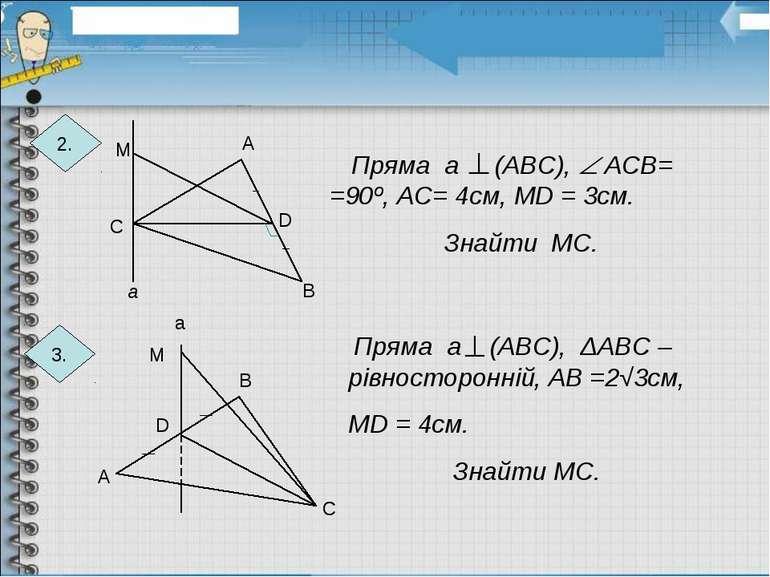
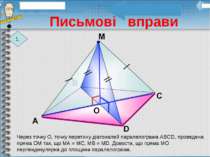
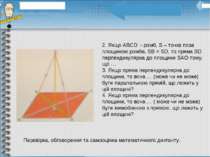
Через точку О, точку перетину діагоналей паралелограма АВСD, проведена пряма ОМ так, що МА = МС, МВ = МD. Довести, що пряма МО перпендикулярна до площини паралелограма. 1. Письмові вправи

2. 3.

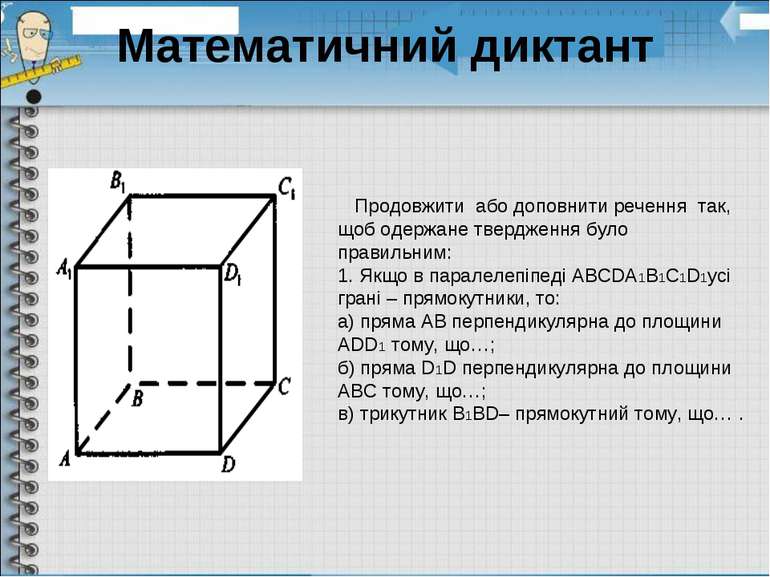
Математичний диктант Продовжити або доповнити речення так, щоб одержане твердження було правильним: 1. Якщо в паралелепіпеді АВСDА1В1С1D1усі грані – прямокутники, то: а) пряма АВ перпендикулярна до площини АDD1 тому, що…; б) пряма D1D перпендикулярна до площини АВС тому, що…; в) трикутник В1ВD– прямокутний тому, що… .

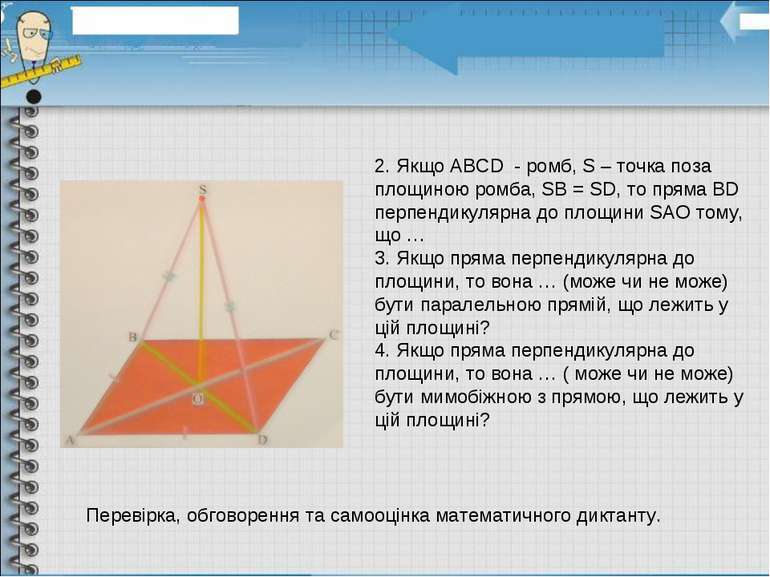
Перевірка, обговорення та самооцінка математичного диктанту. 2. Якщо АВСD - ромб, S – точка поза площиною ромба, SB = SD, то пряма ВD перпендикулярна до площини SAO тому, що … 3. Якщо пряма перпендикулярна до площини, то вона … (може чи не може) бути паралельною прямій, що лежить у цій площині? 4. Якщо пряма перпендикулярна до площини, то вона … ( може чи не може) бути мимобіжною з прямою, що лежить у цій площині?

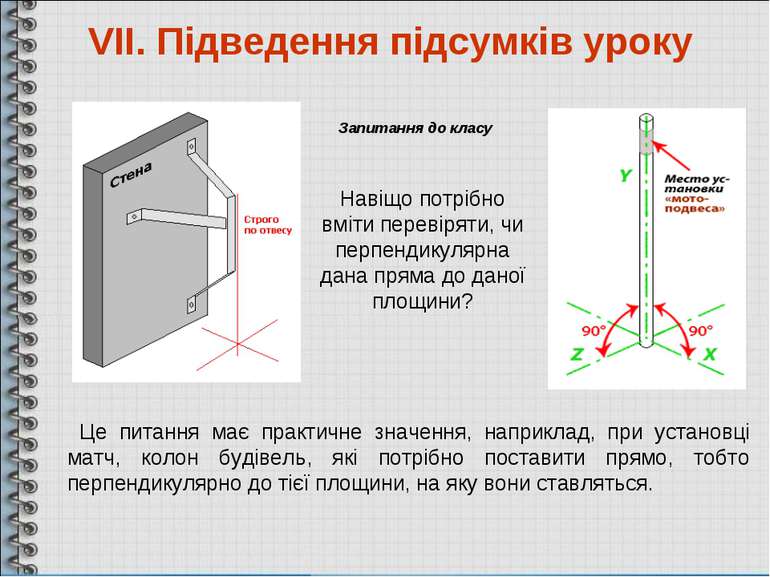
Навіщо потрібно вміти перевіряти, чи перпендикулярна дана пряма до даної площини? VІІ. Підведення підсумків уроку Запитання до класу Це питання має практичне значення, наприклад, при установці матч, колон будівель, які потрібно поставити прямо, тобто перпендикулярно до тієї площини, на яку вони ставляться.

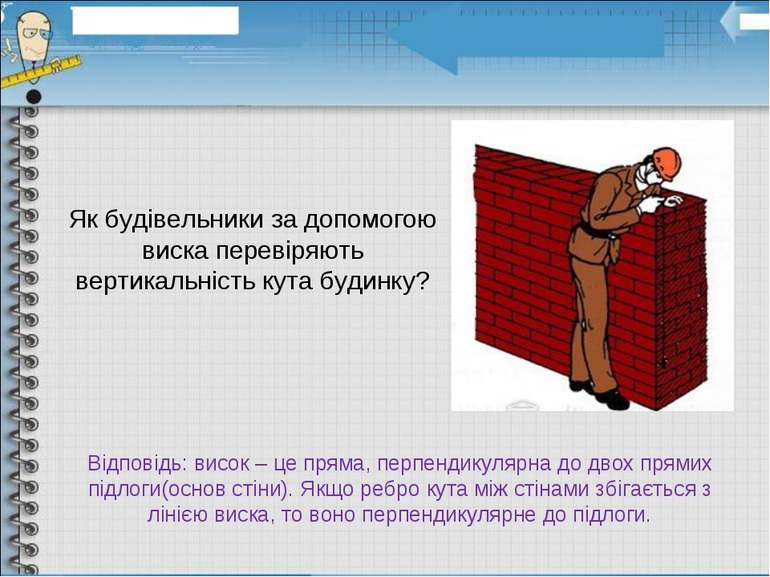
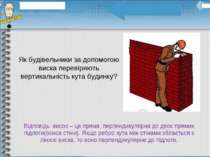
Як будівельники за допомогою виска перевіряють вертикальність кута будинку? Відповідь: висок – це пряма, перпендикулярна до двох прямих підлоги(основ стіни). Якщо ребро кута між стінами збігається з лінією виска, то воно перпендикулярне до підлоги.

VІІІ. Рефлексія ІX. Підсумок уроку Ми закінчили урок, дуже б хотілося побачити ваш настрій, емоції після проведеного уроку. Покажіть смайлик, який підходить вашому емоційному настрою. Метод «Похвали себе» Чи з’явилося почуття самоповаги від своєї роботи на уроці? Чи досягли ви мети, яку поставили на початку уроку? Чи необхідний вивчений матеріал в повсякденному житті? Похвали себе одним реченням. Метод «Чотири Що?» Учні відповідають на запитання: Що нового дізнався на уроці? Що сподобалося найбільше? Що було найскладнішим при виконанні завдань? Що треба ще зробити для досягнення кращих результатів? Дати розгорнуту диференційовану оцінку діяльності учнів на уроці.

X. Домашнє завдання 1. § 29, № 1009, №1027 2. Практичне завдання: виготовити з цупкого паперу і дроту моделі для демонстрації різних розміщень прямих та площин у просторі. 3. Творче завдання: скласти слоган. Наприклад: «Теореми добре будеш знати, будь-які задачі зможеш розв’язати»

Успіхів у навчанні!