Презентація на тему:
Обчислювальна геометрія

Тема «Обчислювальна геометрія» Найпростіші геометричні фігури, їх представлення та властивості Інформатика. 11 клас Лінія АТП

Найпростіші геометричні фігури, їх представлення та властивості Геометрія - наука про властивості геометричних фігур. Починаючи вивчати геометрію, ми знайомилися з різними геометричними фігурами, розглядаючи їхні малюнки. Однак алгоритмізація відмінна тим, що не дає можливості розглядати й аналізувати малюнки. Для виконання алгоритму вхідна інформація задається лише в числовому або символьному вигляді.

Представлення геометричних фігур на площині Серед геометричних фігур на площині можна назвати трикутник, багатокутник, коло тощо. Але найпростішими вважаються точка й пряма. Точка на площині задається двома координатами (х; у), де перший параметр - положення точки відносно осі абсцис Ох, а другий - відносно осі ординат Оу. Обидва параметри задаються цілими або дійсними числами.

Як відомо з математики, пряму на площині можна задати у вигляді загального рівняння: ах + by + с = 0 У деяких задачах обчислювальної геометрії, які передбачають обробку інформації у вигляді прямих на площині, вхідна інформація задається у вигляді трійок чисел (аi, bi, сi) для і = 1, 2, 3, .... n, що визначають коефіцієнти заданих n прямих. Задання прямої

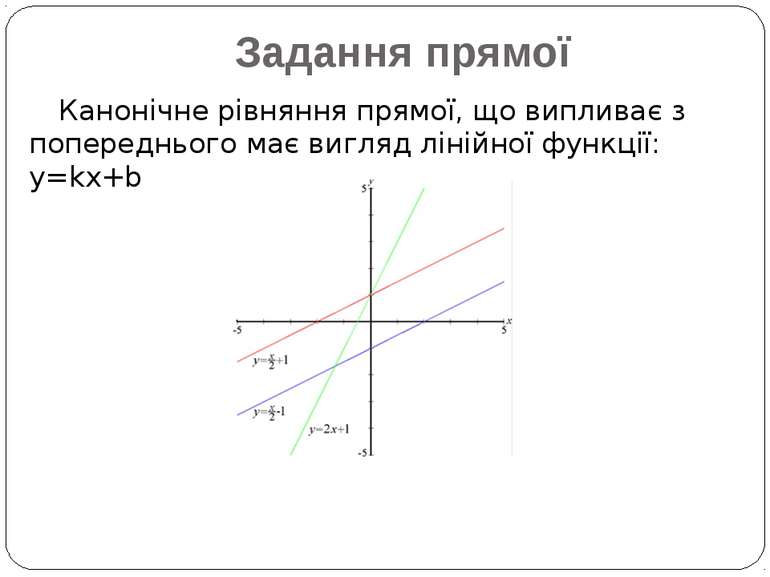
Канонічне рівняння прямої, що випливає з попереднього має вигляд лінійної функції: y=kx+b Задання прямої

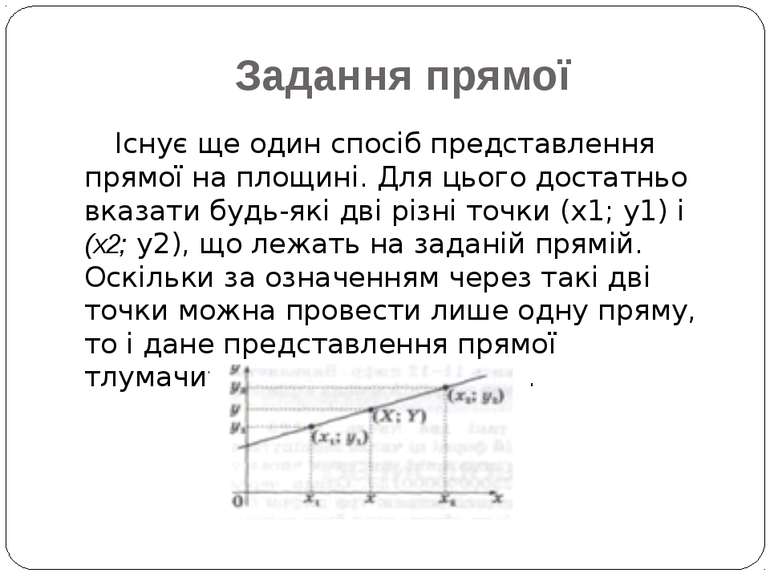
Задання прямої Існує ще один спосіб представлення прямої на площині. Для цього достатньо вказати будь-які дві різні точки (x1; y1) і (х2; y2), що лежать на заданій прямій. Оскільки за означенням через такі дві точки можна провести лише одну пряму, то і дане представлення прямої тлумачитиметься однозначно.

Рівняння прямої Як виглядатиме рівняння прямої, заданої двома точками? Для цього розглянемо задані дві точки (x1; y1) і (х2; y2), і деяку довільну точку (x;y), які лежать на одній прямій (мал. 1). Відповідно до умови подібності можна записати таке відношення: . Звідси рівняння прямої, що проходить через дві задані точки, виглядатиме так:

Розглянемо питання представлення коефіцієнтів a, b, c через координати двох точок (x1; y1) і (x2; y2), розміщених на прямій, яка проходить через них. Це буде корисним для проведення аналізу взаємного розташування заданих точок і прямих, де необхідно буде мати справу з коефіцієнтами загальних рівнянь прямих. Звівши подібні члени в наведеному вище рівнянні, отримаємо:

Відрізок прямої Відрізок прямої на площині задається координатами двох точок (x1; y1) і (х2; y2), що є кінцями цього відрізка. Маючи таку інформацію, можна знайти довжину відрізка за формулою: Координати середини О(x,y) відрізка AB: Координати вектора, що визначається даними точками, можна визначити за формулами: тощо.

Довжина відрізка Варто звернути увагу на обчислення довжини відрізка за цією формулою. Залежно від точності вхідних даних, які можуть бути отримані як результат попередніх обчислень, значення обчисленого квадратного кореня в деяких випадках може дещо відрізнятися. У цьому разі варто не добувати квадратний корінь, а порівнювати квадратні значення довжин відрізків: Такий підхід дасть змогу зменшити кількість виконуваних операцій, що інколи також не менш важливо для покращення оптимізації розв'язання задачі.

Взаємне розміщення двох точок Стосовно заданих відрізків проаналізуємо інформацію щодо їх взаємного розташування на площині дещо пізніше. Про взаємне розміщення двох точок (x1; y1) і (х2; y2) можна говорити для таких випадків:

Взаємне розміщення двох прямих

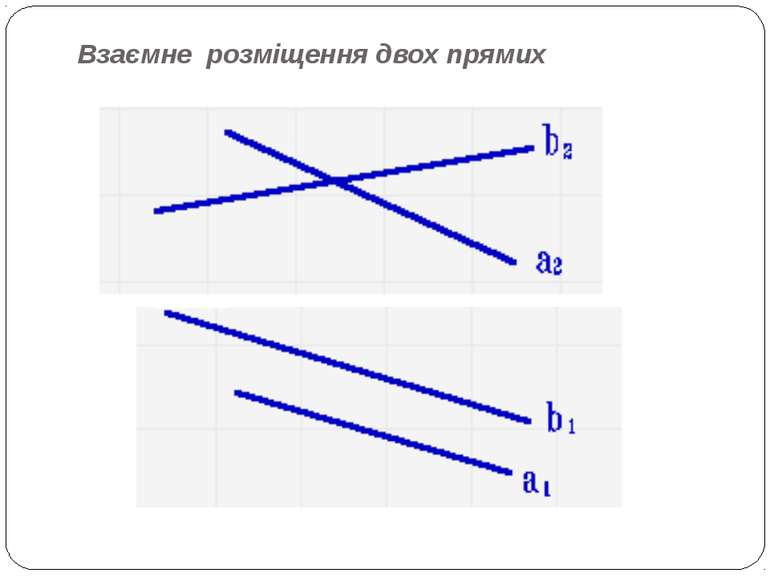
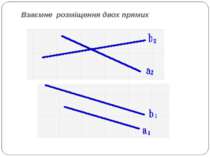
Взаємне розміщення двох прямих Розглянемо взаємне розміщення двох прямих. Розглянемо, чи перетинаються ці прямі, чи вони паралельні, чи обидва ці рівняння представляють одну і ту саму пряму. Знаючи коефіцієнти загальних рівнянь двох заданих прямих (а1, b1, с1) та (а2, b2, с2), можна дати відповідь на всі поставлені запитання. Оскільки при діленні дійсних чисел можна втратити правильну відповідь на точності отриманих результатів, то краще перевірити одночасне виконання таких умов:

Якщо умови збігу та паралельності заданих двох прямих не виконуються, то можна стверджувати, що вони перетинаються. А в цьому разі може виникнути необхідність визначення координат точки перетину таких прямих. Їх можна знайти, розв'язавши систему лінійних рівнянь: На першому кроці з першого рівняння визначимо змінну х через у: Підставимо отриманий вираз у друге рівняння, визначивши значення у через коефіцієнти (а1, b1, с1) та (а2, b2, с2) двох зада них рівнянь прямих: Отриманий вираз для у дасть змогу вивести й аналогічний вираз для х:

Цікавий випадок, коли необхідно проаналізувати взаємне розміщення трьох заданих прямих. Можна почати такий аналіз із будь-яких двох із них і перевірити можливість їх збігання або паралельності. Якщо це так, то розміщення будь якої з них проаналізувати з третьою заданою прямою і зробити відповідний висновок. У випадку, коли перші дві прямі не збігаються і не паралельні, то кожну з них необхідно перевірити на збігання і паралельність з третьою. Тільки після цього можна зробити остаточний висновок щодо їхнього взаємного розміщення. Інколи буває необхідною перевірка умови можливого перетину трьох заданих прямих в одній точці. Для цього необхідно визначити координати точки перетину будь-яких двох із заданих прямих, а потім однієї з них із третьою прямою. Якщо координати обох перетинів, визначені з однаковою точністю, збігаються, то можна з певною ймовірністю стверджувати, що всі три задані прямі перетинаються в одній точці.

Взаємне розміщення точок і прямої Нехай задана пряма загальним рівнянням ах + by + с = 0 та дві точки (x1; y1) і (х2; y2). Ознакою того, що точка (х0; у0) лежить на прямій, є ах0 + bуо + с =0. Якщо точка не лежить на прямій, то зрозуміло, що ах0 + bуо + с 0. А це означає, що значення ах0 + bу0 + с або додатне, або від'ємне. Оскільки пряма ах0 + bу0 + с = 0 ділить координатну площину на дві півплощини, то виявляється, що всі точки (xi; yi), які лежать одній з них, дають однаковий знак виразу ах0 + bу0 + с. Таким чином, можна підбити підсумок наведених міркувань. Якщо для двох заданих точок (x1; y1) і (х2; y2) має місце вираз (ах1 + bу1 + с)(ах2 + bу2 + с)>0, то це означатиме, що ці дві точки лежать по один бік від заданої прямої ах + by+с=0, а якщо (ах1 + bу1 + с)(ах2 + bу2 + с)< 0, то по різні.  

Взаємне розміщення точки і відрізка

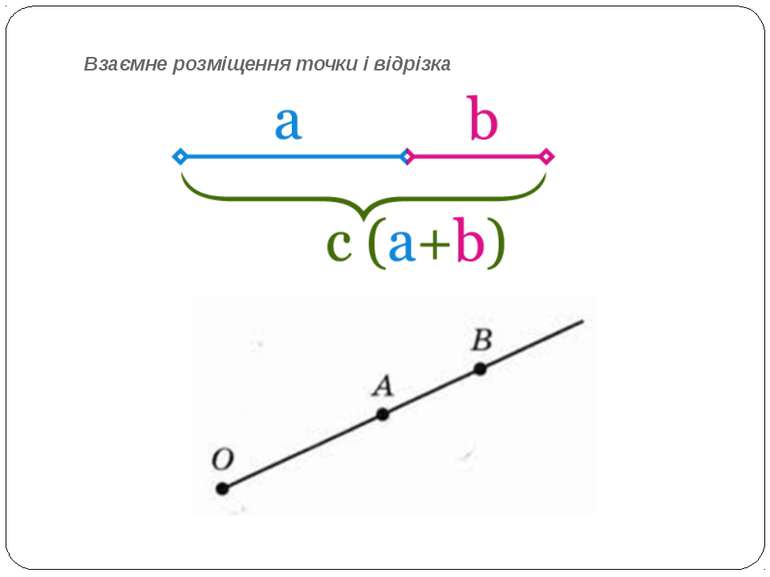
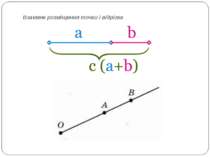
Взаємне розміщення точки і відрізка Нехай задана деяка точка (X; Y) і відрізок прямої з координатами своїх кінців (x1; y1) і (х2; y2). Аналіз взаємного розміщення точки і відрізка полягає в отриманні відповіді на запитання: чи належить точка задано му відрізку? Позитивну відповідь можна отримати лише за на явності виконання таких двох умов: 1). Задана точка (X; Y) належить прямій, що проходить через точки (x1; y1) і (х2; y2); 2). Координати точки (X; Y) належать діапазону, що визначається відповідними координатами кінців заданого відрізка (достатньо перевірити, наприклад, ). Оскільки нам невідомо, де знаходиться координата X заданої точки по відношенню до відповідних координат кінців заданого відрізка x1 , x2, та ще й невідомо, яким чином задано його кінці, то найкращим виходом є порівняння довжин відрізків . На малюнку наведено три можливі варіанти розміщення координат звідки видно, що тільки в разі, коли точка X знаходиться між точками , сума довжин відрізків дорівнює довжині відрізка . .

Надалі переважно розглядатимемо алгоритми, що дають змогу розв'язувати цікаві геометричні задачі на площині. Оскільки вони найчастіше носять практичний характер, то координати точок мають цілочислові та додатні значення. Хоча реалізація обробки вхідної інформації з дійсними значеннями також не виключена, лише варто зазначити, що арифметичні операції з такими числами виконуються дещо повільніше. Щодо від'ємних значень, то, зробивши певні перетворення на площині, а саме перенісши початок координат у точку з найменшим значенням по осі абсцис та найменшим значенням по осі ординат серед відповідних значень усіх заданих точок, можна перейти до обробки додатних значень вхідної інформації. Але це можна робити, лише коли такі перетворення не впливають на результат поставленої задачі.

Практикум  Створити форми для реалізації завдань обчислювальної геометрії усіх розглянутих теоретичних положень. Відредагувати програмний код, виконати програму для різних контрольних значень. Програмний код та контрольні приклади записати у зошит.