Презентація на тему:
Деякі важливі криві на площині

Деякі важливі криві на площині Виконали: Мельник Ірина та Юхименко Інна

Сьогодні математика залишається важливою не тільки як наука, а й знайшла своє місце у нашому повсякденному житті

В наш час математика інтенсивно розвивається. Вона використовує масштабні комп'ютерні методи і знаходить інші об'єкти; проблеми, які здавались важкими, знаходять своє вирішення. І зараз ми познайомимо вас з лише однією частинкою математики – криві четвертого порядку:кардіоїдою, спіраллю Архімеда та лемніскатою Бернуллі.

Кардіоїда Плоска лінія, яка описується фіксованою точкою кола, що котиться по нерухомому колі з таким же радіусом. Отримала свою назву через схожість своїх обрисів зі стилізованим зображенням серця.

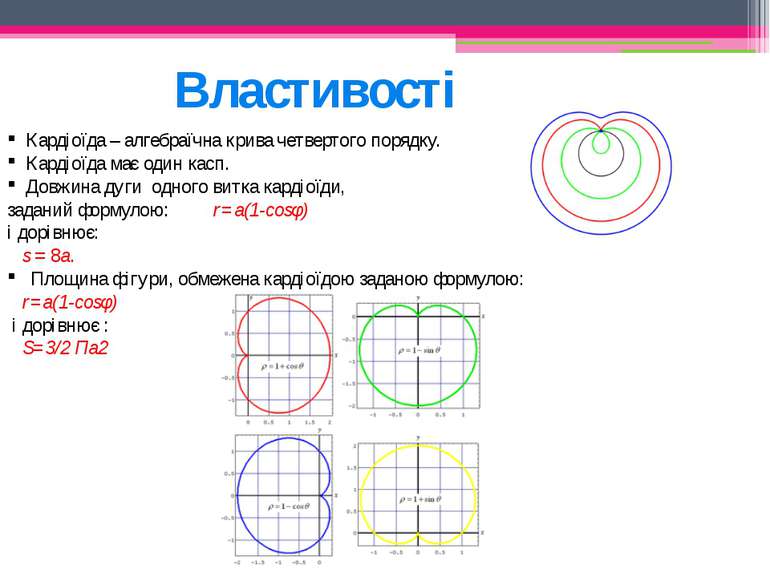
Рівняння прямої у прямокутних координатах: (х2+у2)2-2ах(х2+у2)-а2у2=0 у прямокутних координатах(параметричний запис): x = 2rcost(1 + cost) y = 2rsint(1 + cost) В полярних координатах: r=a(1-cosφ) рівняння в декартових координатах: (х2+у2+2rх)2=4r2(x2+y2)

Кардіоїда – алгебраїчна крива четвертого порядку. Кардіоїда має один касп. Довжина дуги одного витка кардіоїди, заданий формулою: r=a(1-cosφ) і дорівнює: s = 8a. Площина фігури, обмежена кардіоїдою заданою формулою: r=a(1-cosφ) і дорівнює : S=3/2 Па2 Властивості

Кардіоїда є окремим випадком равлика Паскаля та епіциклоїди. Епіциклоїда – це плоска крива, утворена фіксованою точкою кола, яке котиться по зовнішній стороні іншого кола. Равлик Паскаля – це плоска алгебраїчна крива четвертого порядку, конхоїда кола відносно точки на колі.

Історія Кардіоїда вперше зустрічається в працях французького вченого Луї Карре (Louis Carrè, 1705 р.). Назву кривої дав Джованні Сальвеміні ді Кастіллоне (Giovanni Salvemini di Castiglione) в 1741 р. Також незалежно описав кардіоїду голландський математик Й. Коерсма (J. Koersma, 1741 р.). Надалі до кривої виявляли цікавість багато видатні математики XVIII-XIX століть.

«Випрямлення», тобто обчислення довжини кривої, виконав Ла Ір (Philippe de La Hire), який відкрив криву незалежно в 1708 р.   Французький математик і астроном. Опубліковано його праці із зоології, дослідження дихання і фізіологічної оптики. Філіп де Ла Ір ( 1640 - 1718) Історія

Застосування кардіоїди: Кардіоїда використовується у створенні студійних мікрофонів. Скоріше можна сказати, що діаграми напрямленості мікрофона будуть змальовувати це “ серце ”.

Кардіоїда в природі та в повсякденному житті Каустика – складна картинка, світлова фігура (кардіоїда) всередині порожнього, відкритого зверху циліндра при віддзеркаленні світла від його внутрішньої поверхні.

Спіраль Архімеда це траєкторія точки, що рівномірно рухається (з швидкістю V ) вздовж прямої, яка рівномірно обертається (з кутовою швидкістю w) навколо заданої точки – полюса.  

Рівняння Якщо в початковий момент руху точки М і О збігаються і полярна вісь збігається з початковим положенням рухомої прямої, то рівняння спіралі Архімеда у полярних координатах має вигляд ρ = аω.

Історія відкриття спіралі Траєкторія жучка буде мати вигляд даної спіралі, яку в свою чергу відкрив Архімед Уявімо нескінченно довгу секундну стрілку, за якою, починаючи від центру циферблату, невтомно біжить маленький жучок з постійною швидкістю v см / с. Через хвилину жучок буде на відстані 60v см від центру, через дві - 120v і т.д. Взагалі, через t секунд після початку пробігу відстань жучка від центру буде дорівнює vt см.

Основні наукові досягнення вченого — закон Архімеда, принцип важеля (дайте мені точку опори і я поверну Землю) та вчення про центр ваги. Займався оптикою й астрономією. Архімед був також визначним інженером, конструктором низки машин і механічних апаратів. Серед них важіль, клин, блок, нескінченний гвинт і лебідка. Винахід нескінченного гвинта підштовхнув до створення болта, сконструйованого з гвинта і гайки. Архімед ( 287 до н. е.— 212 до н.е.) давньогрецький математик, фізик та інженер, один з найвидатніших вчених античності. Архімедів гвинт

Де в природі ми зустрічаємо Спіраль архімеда? 1 Алое багато листове 2 Броколі романеско 3 Соняшник 4 ..і якщо придивитися, то можна розгледіти її і в неосяжних галактиках

Бачення спіралі в мистецтві Володимир Анатолійович Долгов - російський ІТ менеджер. Генеральний директор Google Russia. Кандидат фізико-математичних наук – змалював її так у своїй картині: “Спираль Архимеда в экстазе Красного петуха”

Застосування спіралі Архімеда: застосування ножів з формою леза у вигляді спіралі Архімеда доцільне при подрібненні м'яса з низьким умістом; Гвинтова поверхня шнекового дозатора,використовується для дозування та порошкоподібних продуктів, наприклад, муки, має форму спіралі Архімеда; Важливим також є той факт, що при обертанні спіралі, вона має гіпнотичні властивості, тому є доцільним її використання в медицині.

Лемніската Бернуллі Плоска алгебраїчна крива. Визначається як геометричне місце точок, добуток відстаней від яких до двох заданих точок (фокусів) незмінне і дорівнює квадрату половини відстані між фокусами.

Рівняння     У прямокутних координатах: (х2+у2)2=2с2(х2-у2) У полярних координатах: р2=2с2сos2φ Параметричне рівняння в прямокутній системі: р2=tg(П/4- φ) Властивості Крива є геометричним місцем точок, симетричних з центром рівносторонній гіперболи щодо її дотичних. Відрізок бісектриси кута між фокальними радіусами-векторами точки лемніскати дорівнює відрізку від центру лемніскати до перетину її осі з цієї бісектрисою. Матеріальна точка, що рухається по кривій під дією однорідного гравітаційного поля, пробігає дугу за той же час, що й відповідну хорду. При цьому вісь лемніскати складає кут 450 вектором напруженості поля, а центр лемніскати збігається з вихідним положенням просувалася точки. Гравітаційна властивість лемніскати

Історія Рівняння лемніскати вперше опубліковано у статті Якоба Бернуллі в 1694 році. Бернуллі назвав цю криву lemniscus. швейцарський математик, основоположник теорій варіаційного числення і диференційних рівнянь, старший із знаменитої династії науковців. Якоб Бернуллі (1654 -1705)  Декількома роками раніше Джованні Кассіні вже досліджував більш загальний випадок, поклавши тим самим початок вивченню еліптичних інтегралів, продовжене згодом Леонардом Ейлером. Деякі властивості кривої були також досліджені Якобом Штейнером у 1835 році

Застосування лемніскати Бернуллі: Цікаво, що Лемніската Бернуллі тепер використовується при побудові трамвайних шляхів у тих місцях, де потяг робить поворот малого радіусу. В стоматології, як деталь у протезних конструкціях зубів.

Де лемніската зустрічається в нашому побуті? 1 Знак нескінченності чи перевернута вісімка 2 3 Чоловій метелик Окуляри

Надіємось, що після нашої доповіді ви ще більше зацікавитесь математикою, не лише,як наукою, а й невід’ємною складовою нашого життя. Дякуємо за увагу