Презентація на тему:
Прикладні задачі аналізу та оцінювання параметрів соціально-економічних процесів

Презентація на тему: Прикладні задачі аналізу та оцінювання параметрів соціально-економічних процесів

План 1. Поняття про модель і моделювання 2. Особливості,принципи математичного моделювання 3. Особливості математичного моделювання економіки 4. Історичний розвиток предмета моделювання

1.Поняття про модель і моделювання Модель - це об’єкт, що заміщує оригіналі відбиває найважливіші риси і властивості оригіналу для даного дослідження, даної мети дослідження за обраної системи гіпотез Математична модель - це абстракція реальної дійсності (світу), в якій відношення між реальними елементами, а саме ті, що цікавлять дослідника, замінені відношеннями між математичними категоріями. Ці відношення зазвичай подаються у формі рівнянь і/чи нерівностей, відношеннями формальної логіки між показниками(змінними), які характеризують функціонування реальної системи, що моделюється

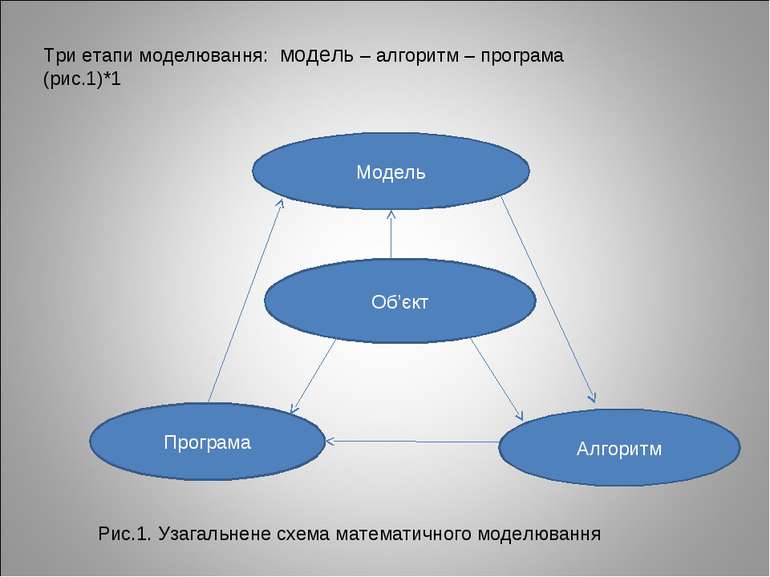
Три етапи моделювання: модель – алгоритм – програма (рис.1)*1 Модель Об’єкт Програма Алгоритм Рис.1. Узагальнене схема математичного моделювання

На першому етапі обирається(чи будується) “еквівалент” об’єкта, що відображає в математичній формі найважливіші (ключові) його властивості – закони, ким він підпорядковується, зв’язки, що притаманні складовим його частинам, тощо. Математична модель (чи її фрагменти) досліджуються теоретичними методами, що дозволяє отримати важливі (концептуального характеру) нові знання про об’єкт. Другий етап – вибір (чи розроблення) алгоритму для реалізації моделі на комп’ютері. Модель подається у формі, зручної для застосування числових методів, визначається послідовність обчислювальних і логічних операцій, котрі необхідно здійснити, щоб отримати шукані величини із заданою точністю. Обчислювальні алгоритми не повинні спотворювати основні властивості моделі, а отже, вихідного об’єкта (оригіналу), бути економними та адаптивними щодо особливостей розв’язання задач і використання компю’терів На третьому етапі створюється програми, що “переносять” модель і алгоритм на доступну комп'ютерну мову. До них також висуваються вимоги економності та адаптивності. Їх можна назвати “електронним” еквівалентом досліджуваного об’єкта, що є придатними для безпосереднього експериментування на компютері.

2. Особливості, принципи математичного моделювання. Головна особливість моделювання полягає у тому, що це метод опосередкованого пізнання за допомогою об’єктів – заміщувачів. Модель постає як своєрідний інструмент пізнання, що його дослідник (системний аналітик) ставить між собою та об’єктом і а допомогою якого вивчає об’єкт, який він цікавить. Саме ця особливість моделювання вивчає специфічні форми використання абстракцій, аналогій, гіпотез, інших категорій і методів пізнання. Необхідність використання моделювання визначається тим, що багато об’єктів (чи аспектів, які стосуються цих об’єктів) безпосередьо досліджувати чи взагалі неможливо, чи це вимагає багато часу і коштів.

Розрізняють такі чотири основні етапи побудови моделі: Перший етап передбачає наявність деяких знань про об’єкт-оригінал. Пізнавальні можливості моделі зумовлюються тим, що модель відображає, з погляду системного аналітика, суттєві риси об’єкта-оригіналу. Питання про необхідність і достатність подібності оригіналу і моделі потребує аналізу. На другому етапі модель постає як самостійний об’єкт дослідження. На третьому етапі здійснюється перенесення знань з моделі на оригінал — формування множини знань S про об’єкт. Цей процес перенесення знань проводиться за певними правилами Четвертий етап — практична перевірка одержаних за допомогою моделей знань та використання їх для побудови узагальнюючої теорії об’єкта чи управління ним. Моделювання — циклічний процес: за першим чотирьохетапним циклом може настати другий, третій тощо. При цьому знання про досліджуваний об’єкт розширюються та уточнюються, а вихідна модель поступово вдосконалюється. .

Загальновизнані вважаються три підходи до побудови математичних моделей. Перший — спрощення реальної ситуації. Суттєве спрощення досягається тоді, коли несуттєві властивості початкової емпіричної стадії пізнання досліджуваного об’єкта та його оточення не враховуються. Другий — побудова простої моделі на підставі певних, найхарактерніших особливостей реальної ситуації, з наступним послідовним ускладненням такої моделі шляхом охоплення інших чинників аж до отримання «прийнятного» варіанта моделі. Третій — введення значної кількості чинників у їхніх взаємозв’язках і побудова та вивчення моделі засобами імітаційного моделювання. У кожному випадку модель «розвивається» та уточнюється у міру досягнення глибшого розуміння системним аналітиком сутності поставленої задачі та об’єкта дослідження.

Принципи концепції «математична модель» деякого об’єкта. Принцип 1. Діалектична пара модель—об’єкт завжди полярна, має два полюси — «модель» і «об’єкт». Принцип 2. З двох взаємопов’язаних полюсів діалектичної пари модель—об’єкт один є первинним, інший — похідний від нього. Принцип 3. Наявності полюса «об’єкт» недостатньо для наявності полюса «модель», наявність полюса «модель» зумовлює необхідність наявності полюса «об’єкт». Принцип 4. Як «модель» для даного «об’єкта», так і «об’єкт» для даної «моделі» семантично та інтерпретаційно багатозначні: «модель» віддзеркалює властивості не одного, а багатьох «об’єктів», «об’єкт» описується не однією, а багатьма «моделями». Принцип 5. «Модель» повинна бути адекватною «об’єктові» й відображати з певною точністю основні його риси та властивості залежно від цілей дослідження, наявної інформації, прийнятної системи гіпотез.

Варто зазначити, що на практиці реалізуються три основні ступені формалізації (формування математичної моделі): змістовний опис; формалізована схема; математична модель. Існують різні форми зображення математичної моделі. Різновид їх обмежується чотирма найтиповішими групами — інваріантною, алгоритмічною, аналітичною, схемною.

Інваріантна форма — зображення математичної моделі безвідносно до методів, за допомогою яких може розв’язуватись поставлена задача моделювання. Приклад інваріантної форми: де а, b, c — відомі характеристики об’єкта; f(Z, p) — відома функція; y(Z, p) — невідома функція.

Алгоритмічна форма — зображення математичної моделі у вигляді послідовності дій, які необхідно виконати, щоб при розв’язанні поставленої задачі моделювання перейти від відомих даних до шуканого результату. Приклад алгоритмічної форми: Визначити значення характеристик об’єкта a, b, c. Обчислити d: Якщо d ? 0, то обчислення значення результату (х, у): .

Аналітична форма — зображення математичної моделі у вигляді формул та співвідношень між математичними виразами, за допомогою яких шукані в задачі моделювання результати визначаються через відомі дані. Приклад аналітичної форми: де a, b — відомі характеристики об’єкта, х — змінна, у — результат.

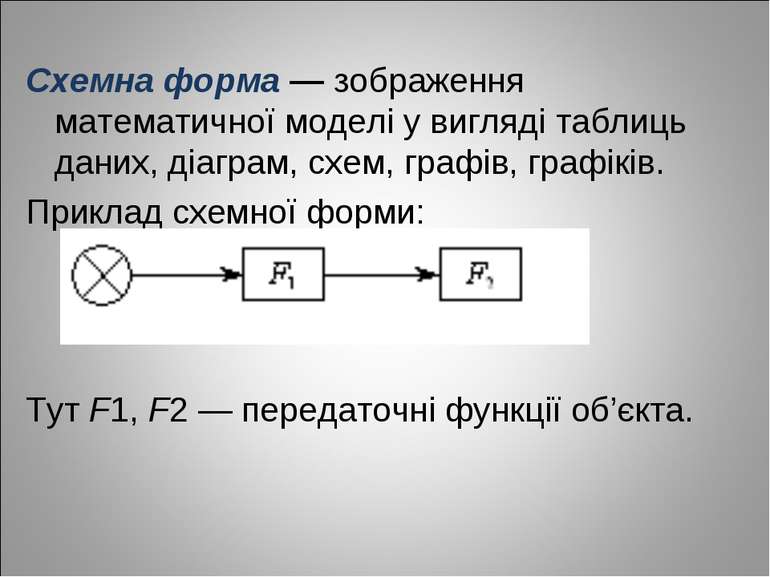
Схемна форма — зображення математичної моделі у вигляді таблиць даних, діаграм, схем, графів, графіків. Приклад схемної форми: Тут F1, F2 — передаточні функції об’єкта.

Ієрархічний підхід до формування моделей. Лише в небагатьох випадках буває зручною і виправданою побудова математичних моделей навіть щодо простих об’єктів відразу в усій повноті, з урахуванням усіх суттєвих чинників. Тому природним є підхід, що реалізує принцип «від простого — до складного», коли наступний крок робиться після досить детального вивчення не дуже складної моделі. Отже, виникає ланцюжок (ієрархія) усе більш деталізованих моделей, кожна з яких узагальнює попередні, включаючи їх як частковий випадок. Зазначимо, що на практиці використовують банк моделей і здійснюють адаптацію відомої моделі.

3. Особливості математичного моделювання економіки 3.1. Основні дефініції та підходи Мистецтво побудови економіко-математичної моделі полягає в тому, щоб узгоджувати якомога більшу лаконічність у її математичному описі з достатньою адекватністю та точністю модельного відтворення тих сторін аналізованої економічної реальності, які, власне, і цікавлять дослідника згідно з цілями та взятими гіпотезами. Моделювання економіки як науковий напрям сформувався у 60-ті роки ХХ століття, хоча має давню й багату передісторію. У його основу, окрім економічних, покладено низку фундаментальних дисциплін (математику, теорію ймовірностей, теорію систем, інформатику, статистику, теорію автоматичного управління тощо).

Під економіко-математичною моделлю розуміють концентроване вираження найсуттєвіших економічних взаємозв’язків досліджуваних об’єктів (процесів) у вигляді математичних функцій, нерівностей і рівнянь. Наголосимо, що математична модель — це об’єкт, котрий створюється системним аналітиком для отримання нових знань про об’єкт-оригінал і відбиває лише суттєві (з погляду системного аналітика) властивості об’єкта-оригіналу.

Аналізуючи сутність зазначеного вище, можна зробити, зокрема, такі висновки: а) будь-яка модель є суб’єктивною, вона несе в собі характерні риси індивідуальності системного аналітика; б) будь-яка модель є гомоморфною, тобто в ній відбиваються (віддзеркалюються) не всі, а лише суттєві властивості об’єкта-оригіналу виходячи з цілей дослідження, узятої системи гіпотез тощо; в) можливе існування множини моделей одного й того самого об’єкта-оригіналу, які відрізняються цілями дослідження, ступенем адекватності тощо.

Модель вважається адекватною об’єкту-оригіналу, якщо вона з достатнім ступенем наближення, на рівні розуміння системним аналітиком модельованого процесу відображає закономірності процесу функціонування реальної економічної системи у зовнішньому щодо об’єкта дослідження середовищі. Більшість об’єктів, що їх вивчає економічна наука, можуть бути охарактеризовані поняттям «складна система». Найпоширенішим є розуміння системи як сукупності елементів, що перебувають у взаємодії та утворюють певну цілісність, єдність. Важливою якістю будь-якої системи є емерджентність — наявність таких властивостей, які не притаманні жодному з її елементів, які складають систему. Тому у вивченні економічної системи недостатньо користуватися методом поділу її на елементи з наступним вивченням цих елементів окремо. Одна з труднощів економічних досліджень полягає у тому, що майже не існує економічних об’єктів, які можна було б розглядати як окремі (несистемні) елементи.

Процес моделювання включає три системотвірних елементи: суб’єкт дослідження (системний аналітик); об’єкт дослідження; модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком).

3.2.. Випадковість і невизначеність економічного розвитку Для методології планування важливе значення має поняття невизначеності економічного розвитку. В дослідженнях з економічного прогнозування і планування розрізняють два типи невизначеності: «істинну», зумовлену властивостями економічних процесів, і інформаційну, пов’язану з неповнотою і неточністю наявної інформації про ці процеси. Істинну невизначеність не можна плутати з об’єктивним існуванням різних варіантів економічного розвитку і можливості свідомого вибору з-поміж них ефективних варіантів. Ідеться про принципову неможливість точного вибору єдиного оптимального варіанта.

У розвитку економіки невизначеність викликається двома головними причинами. По-перше, перебіг планованих і керованих процесів, а також зовнішній вплив на ці процеси не можуть бути точно передбаченими через вплив випадкових чинників і обмеженість людського пізнання в кожний момент. Особливо характерно це для прогнозування науково-технічного прогресу, потреб суспільства, економічної поведінки. По-друге, загальнодержавне планування й управління не лише не всеохоплюючі, але і не всесильні, а наявність множини самостійних економічних суб’єктів з особливими інтересами не дозволяє точно передбачити результати їх взаємодії. Неповнота і неточність інформації про об’єктивні процеси й економічну поведінку підсилює істинну невизначеність. На перших етапах дослідження з моделювання економіки застосовувались в основному моделі детермінованого типу. У цих моделях усі параметри вважалися точно відомими. Однак детерміновані моделі не можна сприймати механічно й ототожнювати з моделями, які позбавлені всіх ступенів вибору (можливості вибору) і мають єдиний допустимий розв’язок. Класичним прикладом жорстко детермінованих моделей є оптимізаційна модель народного господарства, застосовувана для визначення найкращого варіанта економічного розвитку серед множини допустимих варіантів

4. Історичний розвиток предмета моделювання Перші моделі слугували ілюстрацією при дослідженні. 1576 року француз Жан Боден намагається обґрунтувати зміну рівня цін (інфляцію) як результат зміни співвідношення між кількістю грошей і товарів. Ця теорія стає основою монетарної теорії і першою інфляційною моделлю. У 1758 р. французький фізіократ Франсуа Кене (1694-1774) розробляє першу макроекономічну модель господарського кругообігу — "Економічну таблицю" — за аналогією кругообігу людини. Оскільки хвороба є відхиленням від нормального стану людини, то й економічна криза є тимчасовим відхиленням від рівноваги в економіці. А. Сміт (1723-1790) створює класичну макроекономічну модель, яка пояснює процеси саморегулювання ринку через механізм ціноутворення. Д. Рікардо (1772-1823) пропонує модель міжнародної торгівлі. К. Маркс (1818-1883) використовує схематичні моделі для відображення процесу розширеного відтворення.

У XIX ст. свій внесок у моделювання економічних процесів зробили математики — представники неокласицизму англієць Артур Пігу (1877-1959) — "ефект Пігу"; швейцарець Леон Вальрас (1834-1910) — закон загальної економічної рівноваги, теорія економічного добробуту; італієць Вільфредо Парето (1848-1923) — "оптимум за Парето"; австрієць Карл Менгер (1840-1921) — теорія граничної корисності; англієць Френсіс Еджворт (1845-1926) — "скринька Едж-ворта" — модель, яка ілюструє ефективність обміну. Ними створено інструментарій макро- та мікроекономічного аналізу: еластичність попиту, граничний аналіз, коротко- та довгостроковий періоди, взаємозалежність ринків. У їхніх працях сформульовані основні принципи маржиналізму (marginal — граничний). Наприкінці XIX — на початку XX ст. в економічній науці набуває розвитку статистичний напрям, який досліджує та прогнозує циклічний розвиток економіки на основі моделей і методів математичної статистики. Уперше математична статистика була використана в біології англійським ученим К. Пірсоном для вивчення кривих розподілу чисельних характеристик людського організму. В. Парето пропонує статистичні моделі по дослідженню доходів населення в різних країнах. Англійський статистик Гукер розглядає модель взаємозв'язку економічних показників. Він пропонує модель впливу кількості банкрутств на товарній біржі на ціну зерна На початку XX ст. з'являється величезна кількість праць з теорії математичної статистики. Р. Фішер пропонує моделі дисперсійного аналізу, Кобб і Дуглас аналізують виробничі функції.

Світова економічна криза 1929-1933 pp. стає поштовхом створення нової макроекономічної теорії. Англійський економіст Джон Мейнард Кейнс гостро критикує класичну теорію і висуває свої постулати: 1. У ринковій економіці може існувати рівновага за неповної зайнятості. 2. Для усунення неповної зайнятості необхідне втручання держави. 3. Держава втручається в економічні відносини через грошову і бюджетно-податкову політику. 4. Держава впливає на сукупний попит. Фундаментальна праця Д. Кейнса "Загальна теорія зайнятості, процента і грошей" (1936) стає підґрунтям для рівноважних моделей і базовою теорією державного регулювання економіки. Економічні дослідження в СРСР у 20-ті роки проводились під впливом непу (нової економічної політики). Російський учений М. Кондратьєв (1892-1938) висуває теорію великих циклів кон'юнктури ("довгих хвиль") періодичністю 40-60 років. Визначним досягненням радянських учених стала розробка першого у світі балансу народного господарства СРСР за 1923/24 рік. Модель економічного зростання радянського ученого Г. Фельдмана (1884-1958), створена у 1928 p., розкрила взаємозв'язок темпів зростання національного доходу, зміни фондовіддачі і продуктивності праці. Праці Г. Фельдмана були оцінені на Заході лише після Другої світової війни і опубліковані у США 1964 р.

У 30-50 роки відроджується економіко-математичний напрям моделювання. У 1938-1939 pp. ленінградський математик Л. Канторович (1912-1986) сформулював задачі лінійного програмування і запропонував методи їх розв'язання. Моделі радянської економіки створювались на основі економіко-математичних досліджень. Вони охоплювали багаторівневі системи, були досить складними і переважно формальними. Сучасні моделі вирізняються різноманітністю та потужним використанням математичного апарату.