Презентація на тему:
Почленне додавання і множення числових нерівностей

Тема 1 Числові нерівності. Властивості числових нерівностей Поняття числової нерівності. Властивості числових нерівностей Розв’язування вправ. Самостійна робота Почленне додавання і множення числових нерівностей. Розв’язування вправ. Самостійна робота Застосування властивостей числових нерівностей для оцінювання значення виразу

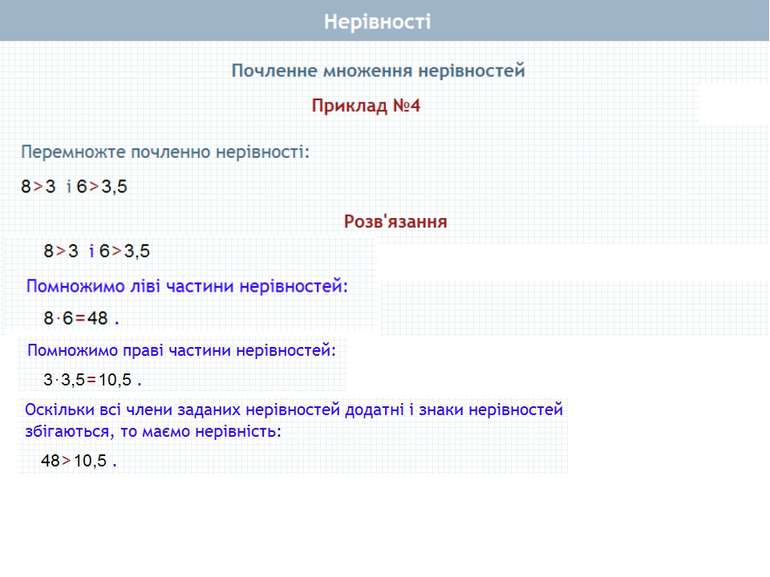
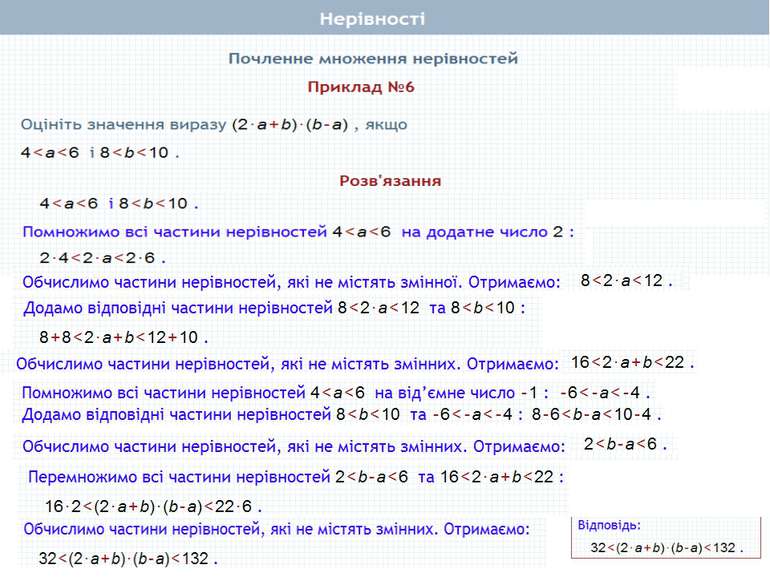
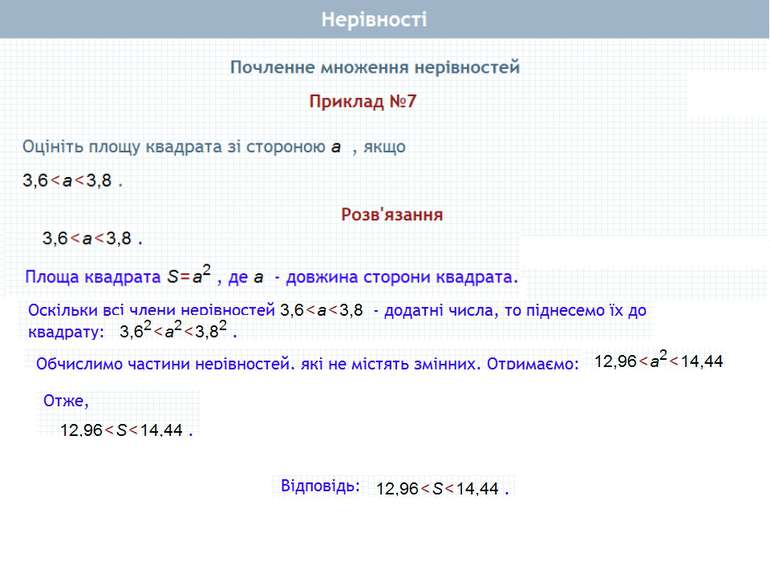
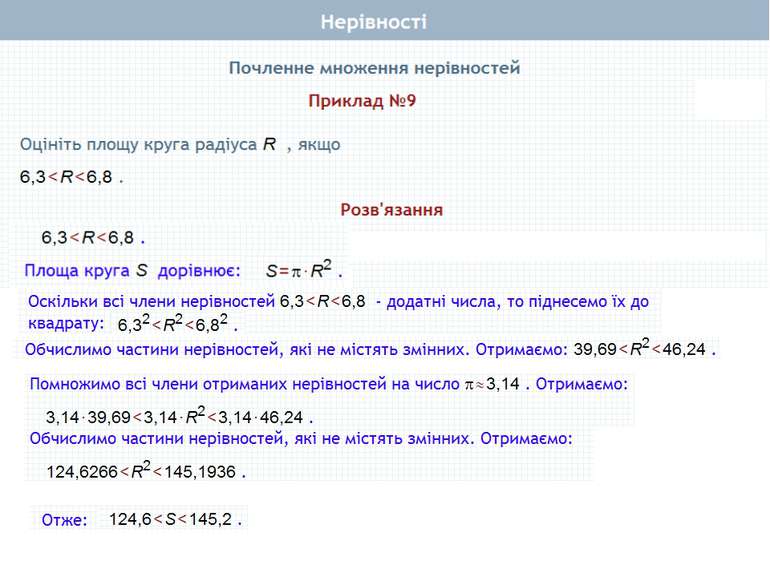
Пункт 1.3. Теорема 1, 2 Почленне додавання нерівностей. Приклади Почленне множення нерівностей. Приклади Почленне додавання і множення числових нерівностей

Пригадайте У чому достатньо пересвідчитись, аби стверджувати, що m>n? Які перетворення обох частин нерівності приводять до нерівності того самого смислу?

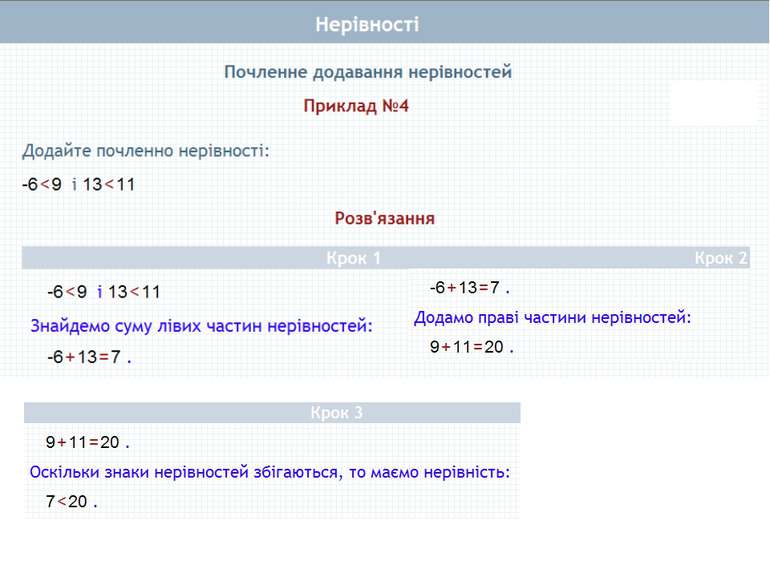
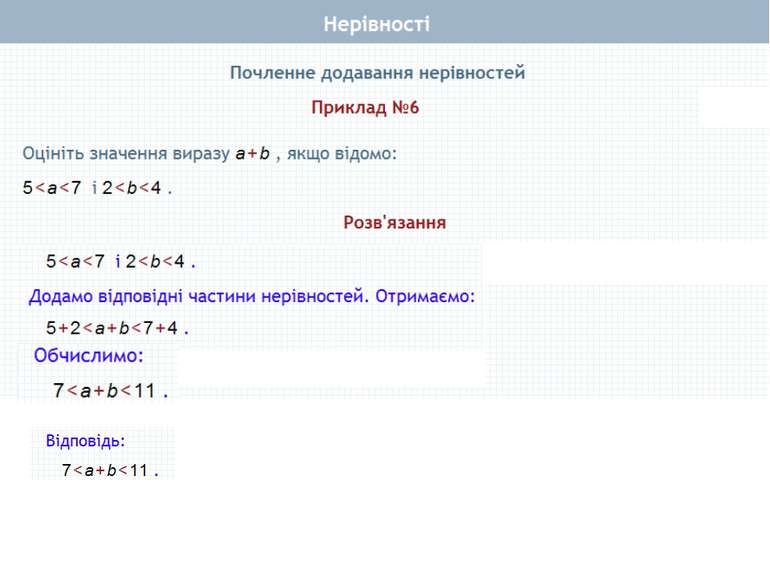
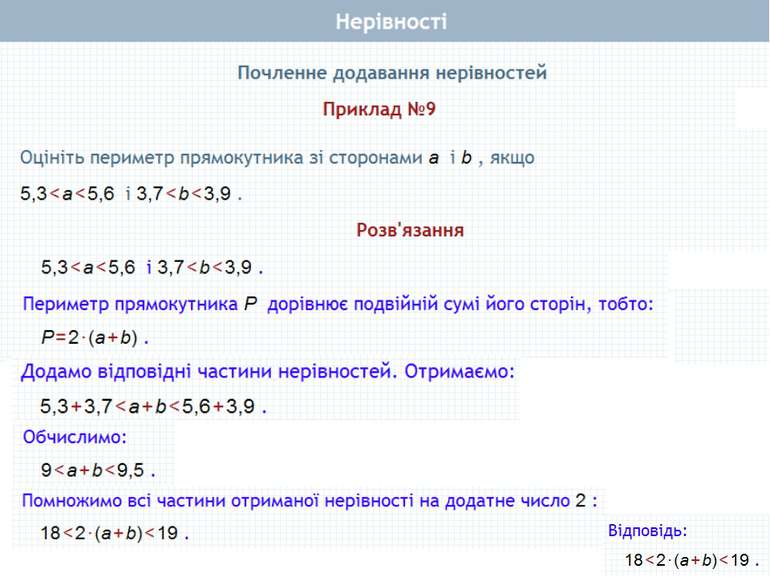
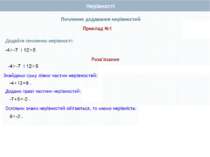
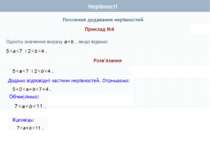
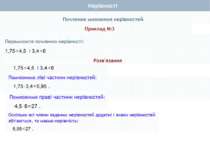
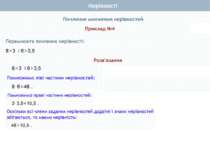
Почленне додавання нерівностей Нехай а > Ь і с > d. Доведемо, що а + с > b + d. Доведення. а > b і с > d (за умовою). Тому a - b > 0 i c – d >0 (за означенням), (a – b) + (c – d) > 0, оскільки сума двох додатних чисел є додатним числом. Перетворимо ліву частину цієї нерівності. Маємо: (а - b) + (с - d) = а - b + с - d = (а + с) - (b + d). Отже, (а + с) - (b + d) > 0, звідки випливає, що а + с > b + d (за означенням). Теорема 1. Нерівності однакового смислу можна почленно додавати, внаслідок чого отримують нерівність того самого смислу.

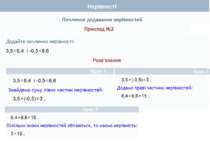
Почленне додавання нерівностей Теорема справджується й у випадку почленного додавання більше двох нерівностей. Теорема 1. Нерівності однакового смислу можна почленно додавати, внаслідок чого отримують нерівність того самого смислу. + + +

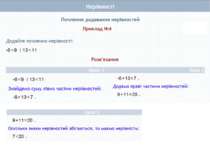
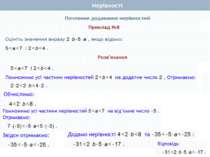
Почленне додавання нерівностей З'ясуємо, чи можна нерівності однакового смислу почленно віднімати. Бачимо, що такі нерівності віднімати не можна, оскільки в результаті не завжди отримаємо правильну нерівність (як у прикладі 2). Теорема 1. Нерівності однакового смислу можна почленно додавати, внаслідок чого отримують нерівність того самого смислу. + - -

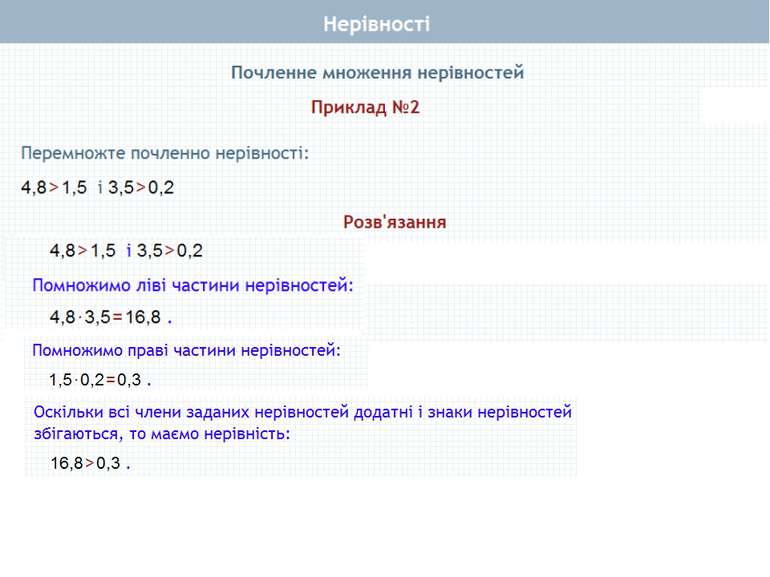
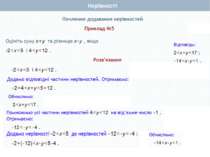
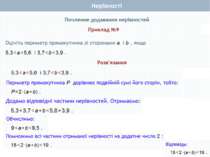
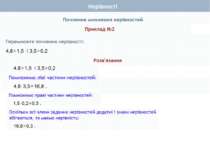
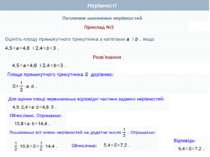
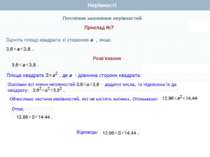
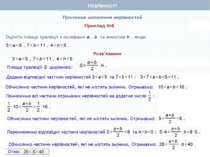
Почленне множення нерівностей Нехай а>b і c>d, а>0, b > 0, с>0, d> 0. Доведемо, що ас > bd. Доведення. Перший спосіб Оскільки а > b і с > 0, то ас > bс (за властивістю 4) . Оскільки с > d і b > 0, то bс > bd (за властивістю 4). Якщо ac>bс i bc>bd, то ac>bd (за властивістю 2). Що й треба було довести Теорема 2. Нерівності однакового смислу можна почленно множити, якщо всі частини нерівностей – додатні. При цьому отримують нерівність того самого смислу.

Почленне множення нерівностей Нехай а>b і c>d, а>0, b > 0, с>0, d> 0. Доведемо, що ас > bd. Доведення. Другий спосіб Для доведення теореми досить показати, що ас - bd > 0. Перетворимо вираз ас - bd, додавши і віднявши від нього bс. Маємо: ac-bd+ bc-bc = (ac-bс) + (bс-bd) = c(a-b)+b(c-d). Визначимо знак отриманого виразу. Маємо: с > 0 (за умовою), а - b > 0, бо а > b; b > 0 (за умовою), с - d > 0, бо с > d. Отже, с(а -b) + b(c - d) = ас-bd> 0. Звідси: ас > bd. Що й треба було довести Теорема 2. Нерівності однакового смислу можна почленно множити, якщо всі частини нерівностей – додатні. При цьому отримують нерівність того самого смислу.

Запитання для самоперевірки На основі якого твердження зроблено остаточний висновок про те, що у доведенні теореми 2 другим способом? Відомо, що Остання нерівність правильна. Отже застереження теореми 2 про те, що всі частини нерівностей мають бути додатні, виходить зайве. Чи ви інакше думаєте? х