Презентація на тему:
Характеристики випадкових величин

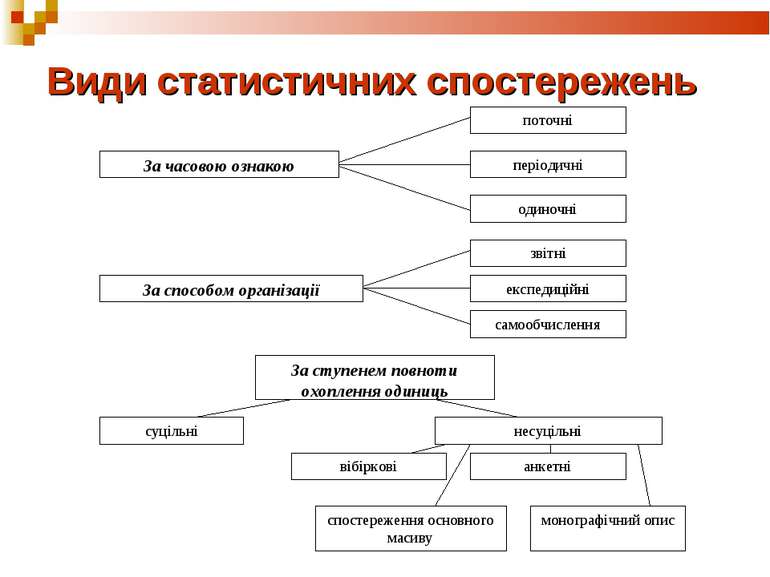
Випадковою називається величина, яка внаслідок випробувань приймає те чи інше (але при цьому лише одне) можливе значення, заздалегідь невідоме, що змінюється від випробування до випробування і залежить від випадкових обставин. На відміну від випадкової події, що є якісною характеристикою випадкового результата випробування, випадкова величина характеризує результат випробування кількісно. Прикладами випадкової величини можуть слугувати розмір случайної величини оброблюваної деталі, похибка результата вимірювання якого-небудь параметра вироба або середовища. Серед випадкових величин, з якими доводиться зустрічатись на практиці, можливо виділити два основних типа: дискретні та неперервні.

Дискретною називається випадкова величина, що приймає кінцеву або нескінчену множину значень. Наприклад: частота влучення при трьох пострілах; число бракованих виробів у партії із N штук; число викликів, що поступають на телефону станцію протягом доби; число відмовлень елементів прибора за певний проміжок часу при випробувані його на надійність; число пострілів до першого влучання в ціль і т. і.

Непрерывною називається випадкова величина, яка може приймати любі значення із деякого кінцевого або нескінченного інтервала. Очевидно, що число можливих значень неперервної випадкової величини нескінчено. Наприклад: похибка при вимірювані дальності радіолокатора; час безвідмовної роботи мікросхеми; похибка виготовлення деталей; концентрація солі у морскій воді і т. і.

Випадкові величини зазвичай позначають буквами X, Y і т. і., а їх можливі значення —x, y і т. і. Для задання випадкової величини недостатньо перерахувати всі її можливі значення. Необхідно також знати, як часто можуть з/явитися ті чи інші її значення у результаті випробувань при одних і тих самих умовах, т. б. потрібно задати ймовірності їх появи. Сукупність усих можливих значень випадкової величини і відповідних їм ймовірностей складає розподіл випадкової величини.

Числові характеристики випадкових величин Середнє значення випадкової величини, або її математичне сподівання : M(X)

Числові характеристики випадкових величин Математичне сподівання дискретної випадкової величини: М(х)=-∞∫+∞хf(x) dx. Математичне сподівання неперервної випадкової величини X, можливі значення якої належать відрізку [a;b] : М(х)=а∫вхf(x) dx.

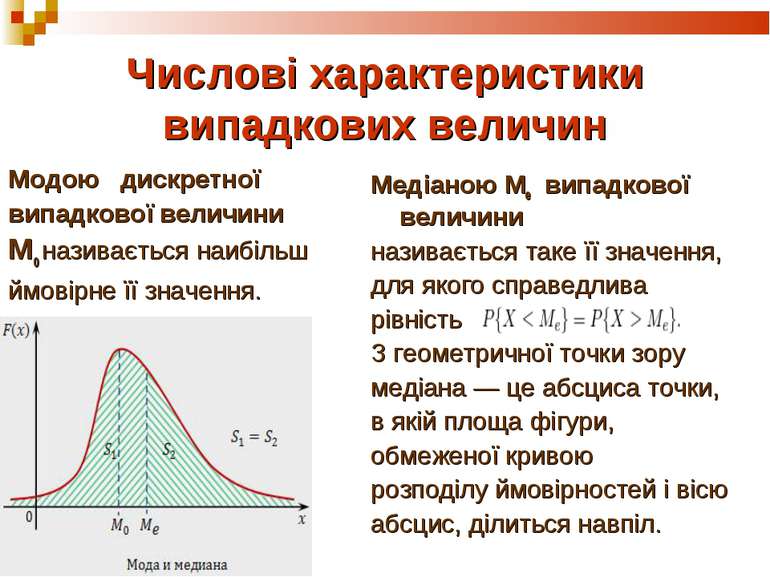
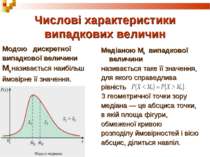
Числові характеристики випадкових величин Модою дискретної випадкової величини Мо називається наибільш ймовірне її значення. Медіаною Ме випадкової величини називається таке її значення, для якого справедлива рівність З геометричної точки зору медіана — це абсциса точки, в якій площа фігури, обмеженої кривою розподілу ймовірностей і вісю абсцис, ділиться навпіл.

Числові характеристики випадкових величин За допомогою дисперсії та її середньоквадратичного відхилення можливо судити про розсіювання випадкової величини навколо математичного сподівання. Мірою розсіювання випадкової величини вважають математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання, яке називають дисперсією випадкової величини X і позначають :

Числові характеристики випадкових величин Для дискретної випадкової величини дисперсія дорівнює суммі добутків квадратів відхилень значень випадкової величини від її математичного сподівання на відповідні ймовірності: Для неперервної випадкової величини, закон розподілу якої задано густиною розподілу ймовірностей f(x), дисперсія дорівнює:

Числові характеристики випадкових величин Середнє квадратичне відхилення випадкової величини обчислюється за формулою:

Поняття про статистику і її методи

Статистика – наука, що збирає, обробляє і вивчає різні дані, пов/язані з різними масовими явищами, процесами, подіями. Предметом вивчення статистики є вивчення кількісної сторони цих явищ.

Статистика вчить, як проаналізувати інформацію, виявити та оцінити закономірності формування, розвитку та взаємодії складних за своєю природою соціально-економічних явищ.

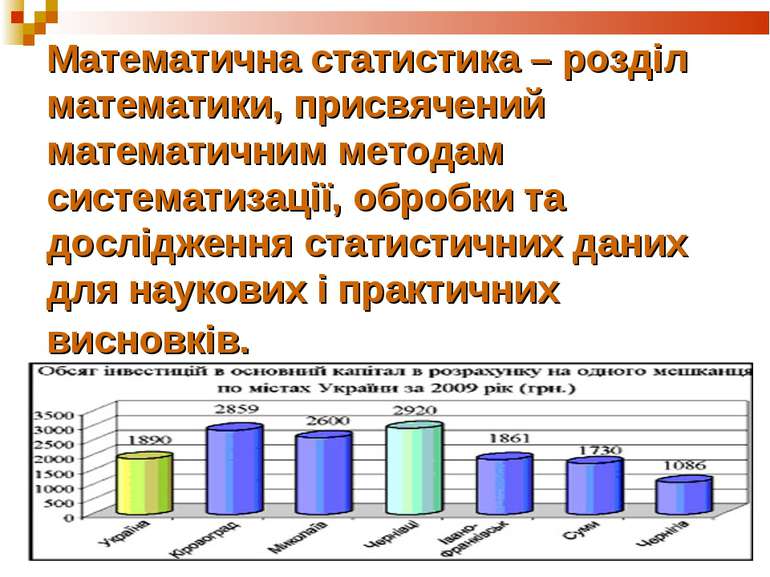
Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки та дослідження статистичних даних для наукових і практичних висновків.

ЇЇ широко застосовують: Соціально-економічні дисципліни

ЇЇ широко застосовують: Астрономія (розподіл і рух зірок у небесному просторі)

ЇЇ широко застосовують: Фізика (термодинаміка)

ЇЇ широко застосовують: Біологія ( закони спадковості)

ЇЇ широко застосовують: Гідрологія (прогноз погоди)

ЇЇ широко застосовують: Індустрія (контроль якості виробів)

Вклад учених у розвиток статистики. Вильям Петті (1625-1687) англійський статистик, економіст, “політичний арифметик”, засновник класичної політекономії.

Вклад учених у розвиток статистики. Пафнутій Львович Чебишєв (1821-1894)

Вклад учених у розвиток статистики. Андрій Андрійович Марков (1856-1922)

Вклад учених у розвиток статистики. Олександр Михайлович Ляпунов (1857-1918)

Вклад учених у розвиток статистики. Карл Фридрих Гаусс (1777-1855)

Вклад учених у розвиток статистики. Ламбе р Адо льф Жак Кетеле (1796-1874)

Вклад учених у розвиток статистики. Фрэнсис Гальтон (1822-1911)

Вклад учених у розвиток статистики. Пірсон Карл (1857-1936)

Вклад учених у розвиток статистики. Романовський Всеволод Іванович (1879-1954)

Вклад учених у розвиток статистики. Слуцький Євген Євгенович (1880-1948)

Вклад учених у розвиток статистики. Колмогоров Андрій Миколайович (1903-1987)

Вклад учених у розвиток статистики. Смирнов Микола Васильович (1900-1966)

Вклад учених у розвиток статистики. Госсет, Уильям Сили (Стьюдент) (1876-1937)

Вклад учених у розвиток статистики. Рональд Эйлмер Фишер (1890-1962)

Вклад учених у розвиток статистики. Джон фон Нейман (1903-1957)

Види статистичних спостережень