Презентація на тему:
Елементи теорії графів алгоритмів

Тема № 2. МАТЕМАТИЧНІ ОСНОВИ ТЕОРІЇ АЛГОРИТМІВ. 2.4 Елементи теорії графів А ну, пізнання людські, подивимося, хто-кого! (Ж.-П. Сартр)

В останні роки теорія графів одержала статус досить актуальної галузі науки. З її допомогою представляється можливим рішення великої кількості задач з області економіки, техніки і безлічі інших сфер людської діяльності. Графи власне кажучи є основними об'єктами, на яких будується сучасна теорія алгоритмів. Особливо важливий взаємозв'язок існує між теорією графів і теоретичною кібернетикою (особливо теорією автоматів, дослідженням операцій, теорією кодування, теорією ігор). Широко використовується теорія графів при рішенні різних задач на обчислювальних машинах. Вірогідно і те, що теорія графів служить математичною моделлю для всякої системи, що містить бінарне відношення.

Леона рд Э йлер (нем. Leonhard Euler; 4 (15) апреля 1707), Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя) — российский и швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

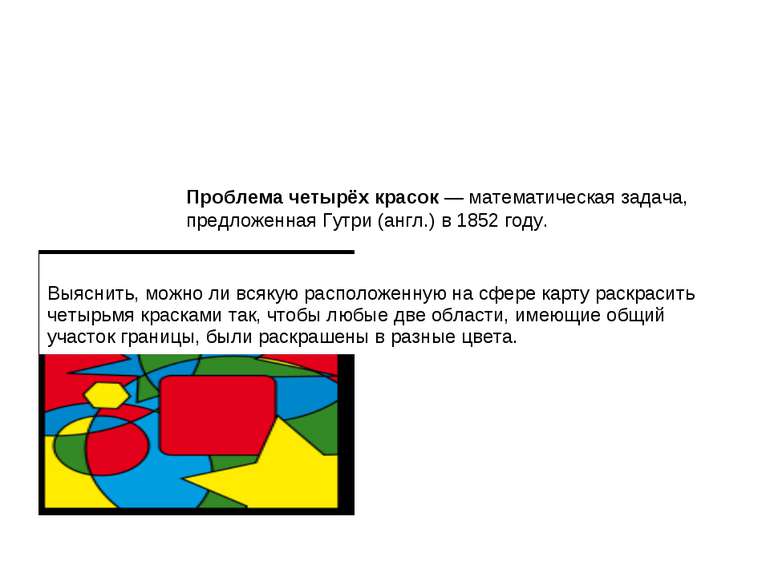
Проблема четырёх красок — математическая задача, предложенная Гутри (англ.) в 1852 году. Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.

Історична ремарка Роком виникнення теорії графів одностайно вважається рік 1736, коли Леонард Ейлер опублікував розв’язок так званої задачі про кенігсберзькі мости, а також знайшов загальний критерій існування ейлерового циклу в графі. Хоча сам термін «граф» вперше з’явився в книзі угорського математика Д.Кьоніга в 1936 році. Отримання дальших суттєвих результатів у цій галузі датують серединою ХIХ століття. Однак початок проведення активних систематичних досліджень та становлення теорії графів як окремішного авторитетного розділу сучасної математики відбулося ще майже 100 років по тому, тобто в середині ХХ століття. Саме з цього часу граф стає однією з найпоширеніших і найпопулярніших математичних моделей у багатьох сферах науки і техніки. Картинка у вигляді набору точок на площині та ліній, проведених між деякими з них, стала зручною і наочною формою зображення найрізноманітніших об’єктів, процесів та явищ

Визначення 2.4.1 . Графом назива-ється модель , де R – бінарне відношення множин V і E, таке, що кожен елемент e E знаходиться в відношенні R або рівно з одним, або рівно з двома елементами множини V. При цьому елементи множини V називаються вершинами графа, елементи множини E називаються ребрами графа, а відношення R – відношенням інцидентності. Вершини, інциденті одному і тому самому ребру, називаються суміжними.

Теорія графів Із суто формальної точки зору граф можна розглядати як один з різновидів алгебраїчної системи (а саме, як модель), а отже, і всю теорію графів як розділ сучасної алгебри. Справді, результати та методи алгебри широко використовуються в теорії графів. Однак за останні півстоліття активного інтенсивного та екстенсивного розвитку теорія графів виробила свою достатньо специфічну власну проблематику і методологію. На сьогодні теорія графів є однією зі складових математичного апарату кібернетики, основною базовою структурною цеглинкою, з яких будується сучасна теорія алгоритмів.

ТЕОРІЯ ГРАФІВ Дещо спрощено відмінність різних підходів до однієї й тієї ж проблеми, пов’язаної з графами, можна продемонструвати на прикладі задачі перевірки ізоморфності двох заданих графів. Класична (абстрактна) теорія алгоритмів констатує, що ця проблема є розв’язною. Класична теорія графів уточнює, що для її розв’язання потрібно перебрати і перевірити не більше, ніж n! варіантів (n кількість вершин в обох графах). Прикладна теорія алгоритмів (і зокрема, її розділ під назвою "Алгоритми на графах") займається конструюванням нетривіальних процедур, що дозволяють визначити, чи є задані графи ізоморфними, і в більшості випадків здійснити цю перевірку достатньо ефективно за рахунок суттєвого скорочення перебору можливих варіантів.

Теорія графів 1. Поняття графа. Способи завдання графів Нехай V деяка непорожня скінченна множина, а V (2) множина всіх двохелементних підмножин (невпорядкованих пар різних елементів) множини V. Графом (неорієнтованим графом) G називається пара множин (V,E ), де E довільна підмножина множини V (2) (E ÍV (2)); позначається G =(V,E ). Елементи множини V називаються вершинами графа G, а елементи множини E ребрами графа G. Відповідно V називається множиною вершин і E множиною ребер графа G. Традиційно ребра {v,w} записуються за допомогою круглих дужок (v,w) (іноді просто vw). Граф, який складається з однієї вершини, називається тривіальним.

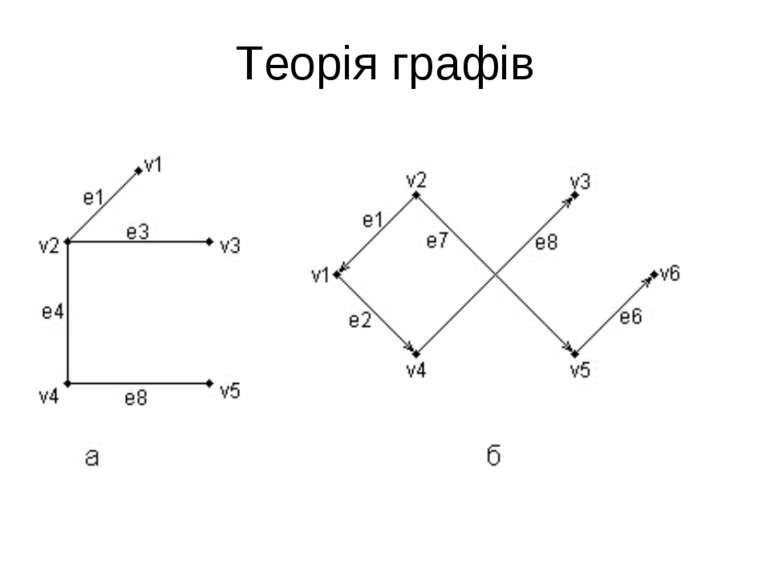
Теорія графів Нехай задано граф G =(V,E ). Якщо (v,w)ÎЕ, то кажуть, що вершини v i w є суміжними, у противному разі вершини v i w є несуміжними. Якщо е=(v,w) ребро графа, то вершини v i w називаються кінцями ребра е. У цьому випадку кажуть також, що ребро е з’єднує вершини v i w. Вершина v і ребро е називаються інцидентними, якщо v є кінцем е. Два ребра називаються суміжними, якщо вони мають спільну вершину. Існує декілька способів завдання графів. Одним зі способів завдання графа G =(V,E ) є завдання кожної з множин V і E за допомогою переліку їх елементів. Приклад 3.1. Граф G1=(V1,E1), V1={v1,v2,v3,v4} і E1={(v1,v3), (v1,v4),(v2,v3),(v2,v4),(v3,v4)} це граф із чотирма вершинами і п’ятьма ребрами. А граф G2=(V2,E2), V2={v1,v2,v3,v4,v5} і E2={(v1,v2),(v2,v4),(v1,v5), (v3,v2),(v3,v5),(v4,v1),(v5,v4)} граф із п’ятьма вершинами і сімома ребрами.

Теорія графів Граф G =(V,E ) зручно зображати за допомогою рисунка на площині, який називають діаграмою графа G. Вершинам графа G ставляться у бієктивну відповідність точки площини; точки, що відповідають вершинам v i w, з’єднуються лінією (відрізком або кривою) тоді і тільки тоді, коли v i w суміжні вершини. Зрозуміло, що діаграма графа змінюватиме свій вигляд у залежності від вибору відповідних точок на площині.

Теорія графів

Теорія графів Графи можна задавати також за допомогою матриць. Занумеруємо всі вершини графа G натуральними числами від 1 до n. Матрицею суміжності A графа G називається квадратна матриця, в якій елемент aij i-го рядка і j-го стовпчика дорівнює 1, якщо вершини vi та vj з номерами i та j суміжні, і дорівнює 0 у противному разі.

Теорія графів Занумеруємо всі вершини графа G числами від 1 до n і всі його ребра числами від 1 до m. Матрицею інцидентності B графа G називається nхm-матриця, в якій елемент bij i-го рядка і j-го стовпчика дорівнює 1, якщо вершина vi з номером i інцидентна ребру ej з номером j, і дорівнює 0 у противному разі.

Теорія графів Нарешті, ще одним способом завдання графів є списки суміжності. Кожній вершині графа відповідає свій список. У список, що відповідає вершині v, послідовно записуються всі суміжні їй вершини. Вибір та зручність того чи іншого зі способів завдання графів залежать від особливостей задачі, яка розв’язується.

Теорія графів . Підграфи. Ізоморфізм графів. Алгебра графів Граф G1=(V1,E1) називається підграфом графа G =(V,E ), якщо V1 ÍV i E1 ÍE. Важливі класи підграфів складають підграфи, які отримуються в результаті застосування до заданого графа операції вилучення вершини і/або операції вилучення ребра. Операція вилучення вершини v з графа G =(V,E ) полягає у вилученні з множини V елемента v, а з множини E всіх ребер, інцидентних v. Операція вилучення ребра e з графа G =(V,E ) це вилучення елемента e з множини E. При цьому всі вершини зберігаються.

Теорія графів Графи G1=(V1,E1) і G2=(V2,E2) називаються ізоморфними, якщо існує таке взаємно однозначне відображення j множини вершин V1 на множину вершин V2, що ребро (v,w)ÎE1 тоді і тільки тоді, коли ребро (j (v),j (w))ÎE2. Відображення j називається ізоморфним відображенням або ізоморфізмом графа G1 на граф G2. Таким чином, ізоморфні графи відрізняються фактично лише ідентифікаторами (іменами) своїх вершин. З точки зору теорії графів ця відмінність не є суттєвою, тому звичайно ізоморфні графи ототожнюють і, зображаючи графи у вигляді діаграм, або зовсім не ідентифікують їхні вершини, або нумерують вершини натуральними числами.

Теорія графів Ізоморфне відображення графа G на себе називається автоморфізмом графа G. Автоморфізм j графа G =(V,E ), при якому для кожної вершини v ÎV виконується j (v)=v, називається тривіальним автоморфізмом. Відношення ізоморфізму є відношенням еквівалентності на сукупності графів. Теорема 2.4.2 Графи G1 та G2 ізоморфні тоді і тільки тоді, коли матрицю суміжності (матрицю інцидентності) одного з цих графів можна одержати з матриці суміжності (матриці інцидентності) іншого графа за допомогою відповідних перестановок рядків та стовпчиків.

Теорія графів Граф G =(V,E ) називається повним, якщо будь-які дві його вершини суміжні (тобто E=V  (2)). Повний граф з n вершинами позначається Kn. Очевидно, що будь-яка підстановка множини вершин повного графа Kn є автоморфізмом цього графа. Тому кількість усіх можливих автоморфізмів графа Kn дорівнює n!

Теорія графів Для графів можна означити операції об’єднання, перетину і доповнення. Об’єднанням графів G1=(V1,E1) і G2=(V2,E2) називається граф G =(V1U V2,E1 U E2); позначається G =G1 U G2. Об’єднання G =G1 U G2 називається прямою сумою графів G1 i G2, якщо V1 V2=Ø. Перетином і різницею графів G1=(V,E1) i G2=(V,E2) з однаковими множинами вершин називаються графи G  =(V,E1 E2) i G  =(V,E1\E2) відповідно; позначаються G  =G1 G2 і G  = G1\G2. Доповненням графа G =(V,E ) називається граф Gd=(V,V  (2) \E ). Отже, граф має ту саму множину вершин V, що і граф G, а вершини графа суміжні тоді і лише тоді, коли вони несуміжні в G. Для графа G з n вершинами виконується Gd=Kn\G. Таким чином можна означити алгебру графів A= (типу (2,2,1)), носієм якої є множина Г всіх графів. Iснують й інші операції для графів, отже, сигнатуру алгебри A можна розширювати.

Теорія графів 3. Графи та бінарні відношення Між множиною всіх графів із множиною вершин V і множиною всіх антирефлексивних симетричних бінарних відношень на V існує взаємно однозначна відповідність: графу G =(V,E ) відповідає відношення R на V таке, що (v,w) R тоді і тільки тоді, коли (v,w) E, v,w  V. Зокрема, порожньому графу G =(V, ) відповідає порожнє відношення на V (R =  ), а повному графу відношення (V  V )\iV, де iV відношення рівності: iV ={(v,v) | v  V  }. Очевидно, що операціям об’єднання, перетину і доповнення графів відповідають аналогічні операції для відношень. Якщо графам G1 i G2 відповідають відношення R1 i R2 то графам G1 G2, G1 G2, Gd відповідатимуть відношення R1 R2 R1 R2 i Gd\iV =(V  V )\(R1 iV). Якщо R транзитивне відношення, то у відповідному графі G для кожної пари ребер (v,w),(w, u) E існує замикаюче ребро (v, u) E.  

Теорія графів 4. Степені вершин графа Степенем d(v) вершини v називається кількість ребер, інцидентних вершині v. Вершина степеня 0 називається ізольованою, а вершина степеня 1 кінцевою (або висячою) вершиною. Кубічним графом називається граф, степені всіх вершин якого дорівнюють 3. Нижченаведені твердження містять прості, але важливі властивості графів. Теорема 3.3. У будь-якому графі G =(V,E ) Σd(v)=2|E |. Справедливість цього твердження випливає з того, що кожне ребро графа інцидентне двом вершинам і, значить, у суму степенів усіх вершин воно вносить дві одиниці. Теорема . У будь-якому графі G =(V,E ) кількість вершин непарного степеня парна. Лема . Кількість ребер у повному графі Kn з n вершинами дорівнює n(n  1)/2.

Теорія графів Маршрутом (або шляхом) у графі G =(V,E ) називається послідовність v1, e1, v2, e2, … , ek, vk +1 вершин vi і ребер ei така, що кожні два сусідні ребра в цій послідовності мають спільну вершину, отже, ei=(vi,vi +1), i=1,2,…,k. Вершина v1 називається початком шляху, а вершина vk +1 кінцем шляху. Всі інші вершини цього шляху називаються проміжними, або внутрішніми, вершинами. Кількість k ребер у маршруті називається довжиною маршруту. Кажуть, що цей маршрут з’єднує вершини v1 і vk +1 або веде з вершини v1 у вершину vk +1. Маршрутом довжини 0 вважається послідовність, що складається з єдиної вершини. Маршрут, в якому всі ребра попарно різні, називається ланцюгом. Маршрут, в якому всі проміжні вершини попарно різні, називається простим ланцюгом.

Теорія графів 9. Деякі важливі класи графів: дерева та двочасткові графи Граф без циклів називається ациклічним. Ациклічний зв’язний граф називається деревом. Довільний ациклічний граф називається лісом. Очевидно, що зв’язними компонентами лісу є дерева, і тому, кожен ліс може бути зображений у вигляді прямої суми дерев. Дерева це особливий і дуже важливий клас графів. Особлива роль дерев визначається як широким їхнім застосуванням у різних галузях науки і практики, так і тим особливим положенням, яке дерева займають у самій теорії графів. Останнє випливає з граничної простоти будови дерев. Часто при розв’язуванні різних задач теорії графів їхнє дослідження починають з дерев. Зокрема, порівнюючи нескладною є проблема перевірки ізоморфності дерев.

Теорія графів Теорема 3.11. Для графа G  =(V,E ), |V |=n, |E |=m такі твердження рівносильні: 1) G дерево (ациклічний зв’язний граф); 2) G зв’язний граф і m =n  1; 3) G ациклічний граф і m = n  1; 4) для будь-яких вершин v і w графа G існує лише один простий ланцюг, що з’єднує v і w ; 5) G ациклічний граф такий, що коли будь-які його несуміжні вершини v i w з’єднати ребром (v,w), то одержаний граф міститиме рівно один цикл.

Теорія графів Наслідок 3.11.1. Для довільного дерева T = (V,E ) з n вершинами виконується Σd(v)=2(n  1). Наслідок 3.11.2. Будь-яке нетривіальне дерево T = (V,E ) має принаймні дві кінцеві вершини. Наслідок 3.11.3. Ліс F, який має n вершин і складається з k дерев, містить n   k ребер. Наслідок 3.11.4. В графі G з n вершинами, який має більше ніж n  1 ребро, є принаймні один цикл.

Теорія графів Кістяковим (каркасним) деревом зв’язного графа G =(V,E ) називається дерево T = (V,ET) таке, що ET    E. Граф називається плоским, якщо його діаграму можна зобразити на площині так, що лінії, які відповідають ребрам графа, не перетинаються (тобто мають спільні точки тільки у вершинах графа). Таке зображення називається плоскою картою графа. Граф називають планарним, якщо він ізоморфний деякому плоскому графу.

Теорія графів Жордановою кривою будемо називати неперервну лінію, яка не перетинає сама себе. Гранню плоского графа назвемо множину точок площини, кожна пара яких може бути з’єднана жордановою кривою, що не перетинає ребер графа. Межею грані будемо вважати замкнений маршрут, що обмежує цю грань. Теорема 3.13. (теорема Ейлера). Для будь-якого зв’язного плоского графа G =(V,E ) виконується рівність |V | |E |+|P |=2. (3.3)

Теорія графів Наслідок 3.13.1. Кількість граней будь-якого плоского укладання зв’язного планарного графа з n вершинами і m ребрами є величиною сталою і дорівнює m  n +2, тобто |P |=|E |  |V |+2. Наслідок 3.13.2. Для довільного зв’язного планарного графа G =(V,E ) з не менше ніж трьома вершинами виконується |E |    3 |V |   6. Наслідок 3.13.3. У будь-якому планарному графі є принаймні одна вершина, степінь якої не перевищує 5. Наслідок 3.13.4. Для довільного планарного графа G =(V,E ) з k компонентами зв’язності виконується |V | |E |+|P |= k +1. (3.4)

Теорія графів 11. Розфарбування графів Нехай G =(V,E ) довільний граф, а Nk={1,2,...,k }. Будь-яке відображення f :V   Nk, яке ставить у відповідність кожній вершині v ÎV деяке натуральне число f (v) ÎNk, називається розфарбуванням графа G. Число f  (v) називається кольором або номером фарби вершини v. Розфарбування f графа G називається правильним, якщо для будь-яких його суміжних вершин v і w виконується f  (v) ¹ f (w). Мінімальне число k, для якого існує правильне розфарбування графа G, називається хроматичним числом графа G і позначається c(G ). Мінімальним правильним розфарбуванням графа G називається правильне розфарбування для k=c(G ). Так склалося історично, що окреме місце в теорії графів займають дослідження з розфарбування планарних графів. Пов’язано це зі славетною проблемою або гіпотезою чотирьох фарб. Згодом з’явилось інше, рівносильне, формулювання гіпотези чотирьох фарб. Для правильного розфарбування вершин довільного планарного графа потрібно не більше чотирьох фарб.

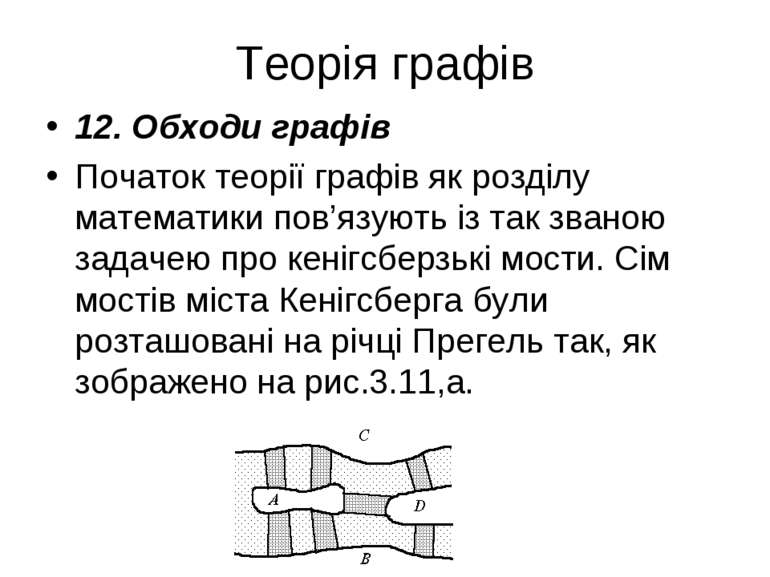
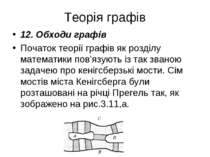
Теорія графів 12. Обходи графів Початок теорії графів як розділу математики пов’язують із так званою задачею про кенігсберзькі мости. Сім мостів міста Кенігсберга були розташовані на річці Прегель так, як зображено на рис.3.11,а.

Теорія графів Цикл, який містить усі ребра графа, називається ейлеровим циклом. Зв’язний граф, який має ейлерів цикл, називається ейлеровим графом. Теорема 3.20 (теорема Ейлера). Зв’язний граф G є ейлеровим тоді і тільки тоді, коли степені всіх його вершин парні. Існує ще один різновид обходу графа, який має різноманітні практичні застосування і називається гамільтоновим циклом. Простий цикл, який проходить через усі вершини графа, називається гамільтоновим циклом. Граф називається гамільтоновим, якщо він має гамільтонів цикл.

Теорія графів 14. Граф як модель. Застосування теорії графів Останнім часом графи і пов’язані з ними методи досліджень використовуються практично в усіх розділах сучасної математики і, зокрема, дискретної математики. Граф є математичною моделлю найрізноманітніших об’єктів, явищ і процесів, що досліджуються і використовуються в науці, техніці та на практиці. Коротко опишемо найвідоміші застосування теорії графів. Наприклад, у вигляді графа можуть бути зображені: електричні і транспортні мережі; інформаційні і комп’ютерні мережі; карти автомобільних, залізничних і повітряних шляхів, газо- і нафтопроводів; моделі кристалів; структури молекул хімічних речовин; моделі ігор; різні математичні об’єкти (відношення, частково впорядковані множини, решітки, автомати, ланцюги Маркова, алгоритми і програми тощо); лабіринти; плани діяльності або плани виконання певних робіт (розклади); генеалогічні дерева тощо.

Теорія графів 14. Граф як модель. Застосування теорії графів Останнім часом графи і пов’язані з ними методи досліджень використовуються практично в усіх розділах сучасної математики і, зокрема, дискретної математики. Граф є математичною моделлю найрізноманітніших об’єктів, явищ і процесів, що досліджуються і використовуються в науці, техніці та на практиці. Коротко опишемо найвідоміші застосування теорії графів. Наприклад, у вигляді графа можуть бути зображені: електричні і транспортні мережі; інформаційні і комп’ютерні мережі; карти автомобільних, залізничних і повітряних шляхів, газо- і нафтопроводів; моделі кристалів; структури молекул хімічних речовин; моделі ігор; різні математичні об’єкти (відношення, частково впорядковані множини, решітки, автомати, ланцюги Маркова, алгоритми і програми тощо); лабіринти; плани діяльності або плани виконання певних робіт (розклади); генеалогічні дерева тощо.